Lissajous, curva di

Lissajous, curva di

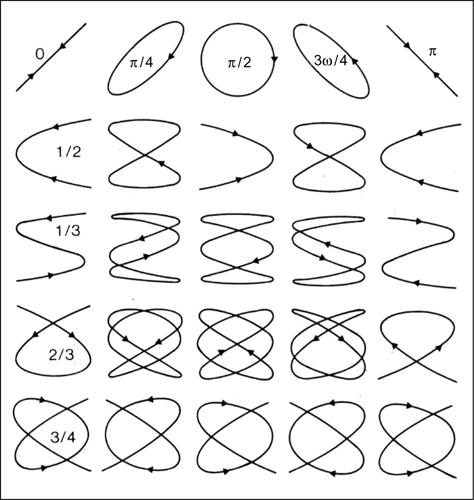
Lissajous, curva di o figura di Lissajous, curva piana di equazioni parametriche x = asin(ht + c), y = bsin(kt + d). È il risultato della composizione di due moti oscillatori ortogonali. La forma di una tale curva dipende dai parametri a, b (che rappresentano le ampiezze di tali moti), h, k (che ne rappresentano le frequenze) e c, d (che ne rappresentano le fasi). Se h = k la curva è un’ellisse. La curva si chiude se e solo se il rapporto h/k è un numero razionale. Prima che da J.A. Lissajous le curve furono studiate dall’astronomo statunitense Nathaniel Bowditch (1773-1838) e sono perciò anche dette curve o figure di Bowditch.