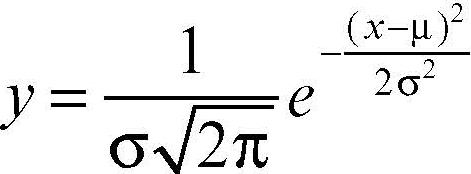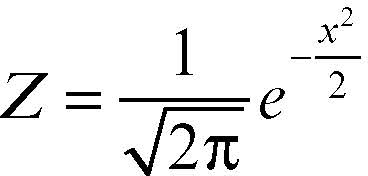curva normale
curva normale
curva normale o gaussiana o curva a campana, in statistica, rappresenta una delle più frequenti distribuzioni empiriche ed è caratterizzata da un andamento a campana in cui i dati della distribuzione osservata partono da zero o da valori molto piccoli fino a raggiungere un massimo e poi diminuire fino a zero o a valori piccolissimi. La curva è il grafico della funzione:
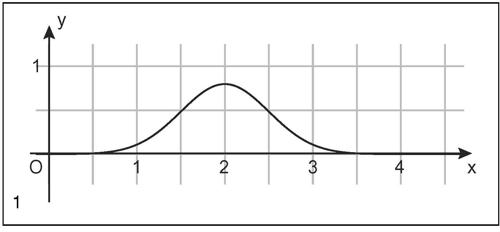
Tale funzione è definita per ogni valore reale di x, assume sempre valori positivi, è simmetrica rispetto alla retta x = μ, in cui assume valore massimo
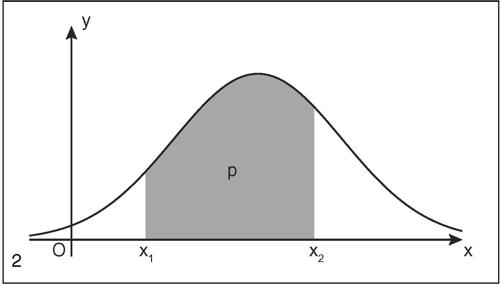
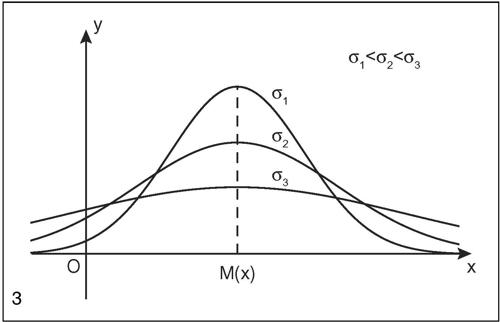
ha come asintoto orizzontale l’asse delle ascisse. L’area della regione di piano compresa tra essa e l’asse delle ascisse è uguale a 1. Per quest’ultimo motivo l’area individuata dalla curva rappresenta l’andamento della funzione di densità di probabilità e le sue particolari caratteristiche fanno sì che la variabile aleatoria caratterizzata da questa funzione di densità prenda il nome di variabile normale e la sua distribuzione (detta distribuzione normale) rappresenti uno dei più importanti modelli statistici. In tale privilegiata interpretazione statistica i parametri μ e σ assumono rispettivamente il significato di media e scarto quadratico medio della variabile. La probabilità che una variabile aleatoria continua X assuma un valore appartenente all’intervallo chiuso [x1, x2] è uguale all’area della regione racchiusa dalla curva, dall’asse delle ascisse e dalle rette di equazione X = x1 e X = x2. La probabilità che la variabile aleatoria normale assuma valori in un intervallo simmetrico rispetto alla media, espresso in termini di unità di scarto quadratico medio, è costante. In particolare, in una distribuzione normale circa i due terzi (68,27%) dei casi cadono nell’intervallo (μ − σ, μ + σ), il 95,45% dei casi nell’intervallo (μ − 2σ, μ + 2σ) e la quasi totalità di essi (99,73%) cade nell’intervallo (μ − 3σ, μ + 3σ). Le variazioni alla forma caratteristica della curva, a parità di valore medio, dipendono essenzialmente dal valore dello scarto. Quanto più è grande lo scarto quadratico medio tanto maggiore è la dispersione e quindi la curva risulta più schiacciata; tale fatto, nella rappresentazione grafica, determina una maggiore apertura della “campana”; la diversa apertura è denominata curtosi.
È spesso utile, per le inferenze e i confronti statistici, considerare la curva normale standardizzata che si ottiene operando la trasformazione:
Tale nuova variabile X′ è spesso indicata con Z, è detta variabile normale standardizzata ed è caratterizzata dai parametri μ = 0 e σ = 1. La sua espressione analitica è:
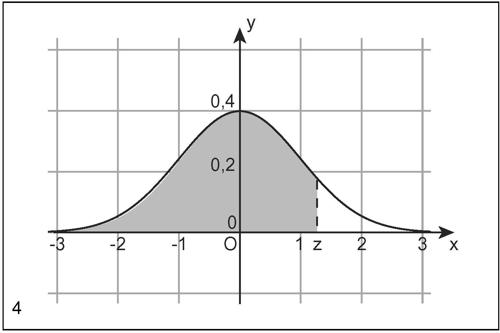
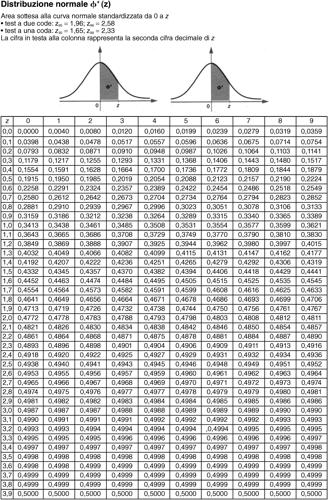
La sua funzione di ripartizione, indicata con Φ(z) (si legge «phi di zeta»), fornisce la probabilità che la variabile normale standardizzata Z abbia valore minore o uguale a z: Φ(z) = p(Z ≤ z). Si ha per esempio Φ(0) = 0,5 (dato che l’area sottesa a tutta la curva è uguale a 1); i valori di tale funzione si trovano in apposite tavole della distribuzione normale (si veda la tavola relativa).
Poiché gli errori di misura si distribuiscono in modo normale e quindi la loro distribuzione discreta, rappresentata graficamente, è approssimata da tale curva, essa prende anche il nome di curva degli errori.