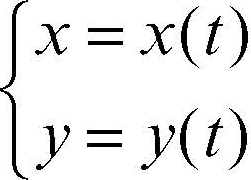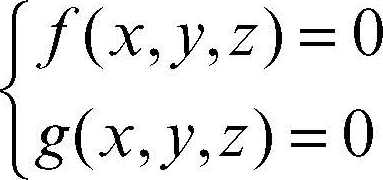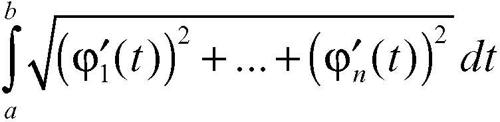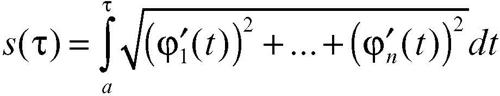curva

curva

curva termine che indica in generale una linea qualsiasi, inclusa la retta. Più precisamente, una curva può essere costituita da una linea oppure da più linee, ciascuna delle quali è detta → ramo della curva. Il significato del termine «curva» ha subito una notevole evoluzione nella storia della matematica: dall’insieme di dimensione 1 di punti che soddisfano certe proprietà geometriche, all’insieme di punti le cui coordinate, associate a un dato sistema di riferimento, soddisfano una certa equazione. Se tutti i punti della curva appartengono a uno stesso piano viene detta curva piana, altrimenti è detta curva sghemba o gobba. Inoltre, una curva è detta chiusa se partendo da un suo qualsiasi punto, percorrendola sempre nello stesso verso, si torna al punto di partenza, altrimenti è detta aperta.

Curve piane

In geometria analitica, una curva piana, riferita a un sistema di assi cartesiani, può essere rappresentata da un’equazione del tipo ƒ(x, y) = 0 o del tipo y = ƒ(x), dette, rispettivamente, equazione cartesiana implicita ed equazione cartesiana esplicita della curva. Una curva piana può essere assegnata anche mediante equazioni parametriche del tipo

dove le due funzioni non sono entrambe costanti al variare di t in R. Se l’insieme di base (dominio) in cui varia il parametro è un intervallo, la rappresentazione parametrica induce un orientamento della curva, trasportando l’orientamento naturale dell’intervallo base; ciò è conforme alla nozione intuitiva di “traiettoria” percorsa da un punto mobile quando si pensa al parametro come “tempo”.

Più propriamente, la curva può essere definita come il sottoinsieme dei punti di un piano affine, metrico o proiettivo, le cui coordinate soddisfano l’equazione data (per accentuare l’attenzione alla curva come ente astratto e alla sua rappresentazione come ente geometrico, si indica tale insieme dei punti come supporto o sostegno o immagine della curva).

Lo scostamento dall’andamento rettilineo di una curva in un punto è detto → curvatura della curva in quel punto, generalmente indicata con κ, ed è uguale a 1/R, essendo R il raggio di curvatura, cioè il raggio del → cerchio osculatore della curva in quel punto.

Le curve piane vengono classificate in base alle equazioni che le rappresentano. Una curva di equazione cartesiana ƒ(x, y) = 0 è algebrica se può essere ridotta a un’espressione polinomia in x ey uguagliata a 0, cioè a un polinomio P_n(x, y) in x e y a coefficienti in un campo (per esempio R); è trascendente se la sua equazione non può essere ridotta a un polinomio. In una curva algebrica, il grado n del polinomio (grado complessivo nelle due variabili) è detto ordine della curva: esso rappresenta il numero di punti, eventualmente complessi o impropri, che la curva ha in comune con una retta qualsiasi del piano, cioè coincide con il massimo numero di intersezioni che la curva può avere con una retta. Le curve algebriche del primo ordine sono le rette, quelle del secondo ordine le coniche, quelle del terzo ordine le cubiche (cissoide di Diocle, folium di Cartesio, versiera di Agnesi, strofoide ecc.); sono curve del quarto ordine, per esempio, l’ovale di Cassini, la lemniscata di Bernoulli, la lumaca di Pascal, la concoide di Nicomede ecc., mentre è curva del sesto ordine, per esempio, l’asteroide. Sono curve trascendenti le curve rappresentate da funzioni goniometriche, esponenziali, logaritmiche, iperboliche (la cicloide, la sinusoide, la trisettrice di Ippia, la cocleoide ecc.).

Se P_n(x, y) si può scomporre nel prodotto di k polinomi irriducibili di rispettivi gradi n₁, n₂, ..., n_k, la curva si spezza in k curve di rispettivi ordini n₁, n₂, ..., n_k tali che n₁ + n₂ + ... + n_k = n; se ciò accade la curva è detta riducibile, altrimenti viene detta irriducibile.

Nel piano proiettivo complesso una curva algebrica di ordine n, rappresentata da un polinomio omogeneo di grado n, uguagliato a zero, ha esattamente n punti (contati con la dovuta molteplicità di intersezione) in comune con una retta generica che non sia una componente della curva. Un punto P ottenuto per s distinti valori del parametro delle equazioni parametriche che descrivono la curva, è detto punto multiplo di molteplicità s o, più semplicemente, punto s-plo. Un punto con molteplicità 1 è detto punto semplice. Una curva costituita solo da punti semplici è detta curva semplice. Una curva piana chiusa e semplice è detta curva di Jordan.

Tangente a una curva

Data una curva piana in equazione cartesiana y = ƒ (x), la retta tangente a essa in un suo punto P₀(x₀, y₀) ha equazione

mentre la normale (retta perpendicolare) in P₀(x₀, y₀) ha equazione

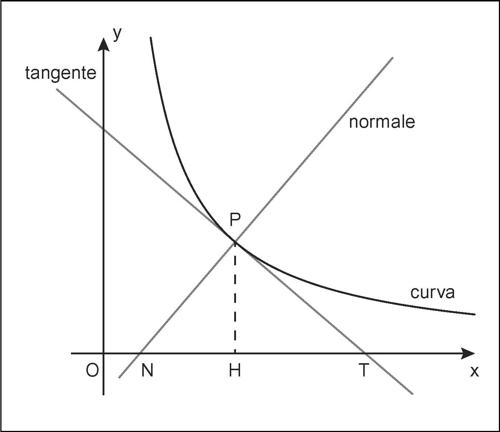
Con riferimento alla figura, dette rispettivamente N e T le intersezioni della tangente e della normale in P con l’asse della ascisse e H la proiezione di P sul medesimo asse, le misure con segno dei segmenti orientati HT e HN vengono dette, rispettivamente, sottotangente e sottonormale.

Una curva dotata in ogni punto di tangente è detta curva regolare. La proprietà di una curva di essere regolare equivale al suo essere rappresentata da → funzioni differenziabili.

Si definisce angolo di due curve passanti per uno stesso punto P l’angolo formato dalle loro rispettive tangenti in P. In particolare, se le due curve hanno la stessa tangente si dicono tangenti in P. Due curve tangenti in un punto P hanno contatto di ordine k se le rispettive funzioni e le loro derivate fino all’ordine k assumono lo stesso valore in P, mentre assumono valori diversi le derivate di ordine k + 1. Due curve aventi in un dato punto P contatto di ordine k ≥ 1 sono dette tra loro tangenti. Una retta si dice bitangente a una curva se è tangente a essa in due punti distinti. Analogamente per due curve. Per esempio una circonferenza avente per diametro uno dei due diametri principali di un’ellisse risulta a essa bitangente.

Per un punto s-plo di una curva passano esattamente s rette aventi contatto in almeno (s + 1)-punti con la curva o, come si preferisce dire, di ordine s con la curva. Le s rette vengono dette tangenti principali alla curva in quel punto. Se le s tangenti sono distinte, P è detto punto s-plo ordinario. Ogni punto di molteplicità s ≥ 2 è un punto di singolarità, intendendo con tale locuzione ogni punto in cui una curva ha un comportamento particolare: punto di discontinuità, punto isolato, punto multiplo ecc. Un punto con molteplicità 2 è detto punto doppio e costituisce il nodo di una curva, con i relativi sottotipi classificati in base alle sue proprietà locali (→ curva, nodo di una).

Il luogo delle tangenti ai punti di una curva piana è detto inviluppo della curva ed è esprimibile mediante una equazione omogenea in coordinate plückeriane di retta. Il grado di tale equazione è detto classe della curva e uguaglia il numero di tangenti alla curva che si possono condurre da un generico punto del piano. Oltre alla classe, le altre proprietà proiettive delle curve algebriche piane sono l’ordine (già definito sopra come numero dei punti intersezione con una retta generica del piano), e il genere: viene detto genere di una curva algebrica irriducibile di ordine k e dotata di d punti doppi, il numero

La principale proprietà del genere di una curva consiste nel fatto che esso non viene alterato da una qualsiasi trasformazione isomorfa della curva stessa (due curve si dicono isomorfe se a ogni punto non singolare dell’una corrisponde uno e un solo punto dell’altra).

Curve sghembe

Una curva sghemba nello spazio tridimensionale viene rappresentata, in forma implicita, da equazioni del tipo

In tal modo la curva viene rappresentata come insieme dei punti dello spazio intersezione di due superfici algebriche. Assumendo come parametro l’ascissa curvilinea s, cioè la lunghezza del tratto di curva compreso tra un punto fisso (origine) e un punto generico, una curva sghemba può essere rappresentata dalle seguenti equazioni parametriche: x = x(s), y = y(s), z = (s) (parametrizzazione naturale). Analogamente a quanto avviene per una curva piana, la tangente a una curva sghemba in un suo punto P si ottiene come posizione limite della retta PQ, al tendere del punto Q al punto P lungo la curva. Il piano osculatore a una curva sghemba in un suo punto P si ottiene come posizione limite del piano passante per la tangente in P e per un punto Q della curva, al tendere di Q a P. Il cerchio osculatore a una curva sghemba in un suo punto P è la posizione limite del cerchio contenuto nel piano osculatore e passante per P, Q, R, al tendere di Q e R a P.

Curve in Rn

Più in generale, si definisce curva l’ente astratto assegnato per mezzo di una funzione φ definita su un insieme E (insieme base) di numeri reali e a valori nello spazio euclideo n-dimensionale Rⁿ, φ: E → Rⁿ. Tale funzione esplicitata rispetto alle sue componenti φ₁, φ₂, ..., φ_n dà le equazioni parametriche della curva:

Generalmente, si formula l’ipotesi che la funzione φ sia continua e che l’insieme base sia un intervallo chiuso, I = [a, b]; se le φ_i sono date da rapporti di polinomi la curva si dice razionale. Tramite la rappresentazione parametrica resta determinato un orientamento della curva, trasportando l’orientamento naturale dell’intervallo base I. Una curva si dice chiusa su I = [a, b] se φ(a) = φ(b); se essa non è chiusa, i punti corrispondenti agli estremi dell’intervallo base si dicono estremi della curva. Punto semplice è ogni punto della curva che non corrisponde a due diversi valori del parametro (esclusi gli estremi dell’intervallo base); curva semplice è una curva tutti i punti della quale sono semplici. Punto multiplo di ordine s è un punto che corrisponde a s distinti valori del parametro (esclusi ambedue gli estremi). Una curva si dice regolare se ammette una rappresentazione parametrica φ derivabile con derivate continue e non simultaneamente nulle (tranne che in punti isolati dell’intervallo I). Si dice regolare a tratti se l’intervallo base è scomponibile nell’unione di un numero finito di sottointervalli in ciascuno dei quali la corrispondente porzione (o arco) di curva è regolare.

La lunghezza della curva regolare nell’intervallo [a, b] è il numero:

Si definisce ascissa curvilinea la funzione:

È possibile parametrizzare una curva mediante la ascissa curvilinea ottenendo ancora la stessa orientazione data da φ se si denota con ψ(s) quel punto della curva distante (lungo la curva stessa) s da φ(a), ossia ponendo ψ(s (τ)) = φ(τ) per ogni τ di I.

Assumendo la rappresentazione parametrica mediante l’ascissa curvilinea si possono esprimere per una curva dello spazio tridimensionale tre tipi di versori. Il versore tangente è dato da

essendo x₀ = ψs₀) un punto della curva; la norma della derivata del versore tangente, detta flessione o prima curvatura e designata come{{{1}}}/R (a volte però indicata con C) essendo R il raggio di curvatura, indica di quanto la curva si discosta dall’andamento rettilineo in prossimità di un punto x₀ = ψ(s₀). Il versore normale principale è dato da

Il versore binormale è dato da b = t × n (in cui × indica il prodotto vettoriale), la norma della derivata del quale, detta torsione assoluta della curva stessa, indica di quanto essa si discosta dall’andamento piano.

I tre versori t, n, b, se la curva non ha un flesso in x₀, sono mutuamente ortogonali e individuano il triedro fondamentale (→ terna intrinseca) relativo al punto x₀; le rispettive derivate sono legate tra loro dalle formule di → Frenet. Nel caso particolare di una curva piana del piano x₁x₂, il versore binormale è costante e ha la direzione dell’asse x₃.

Per una curva algebrica sghemba, le principali proprietà proiettive sono l’ordine (numero dei punti intersezione con un piano generico), la classe (numero dei → piani tangenti passanti per una retta generica), il rango (numero di → piani osculatori passanti per un punto generico).