Lame, curve di

Lame, curve di

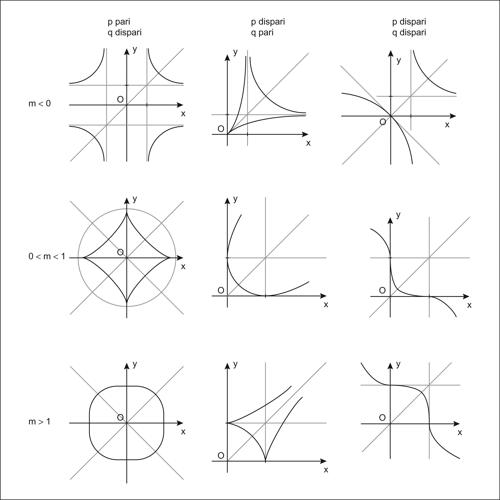
Lamé, curve di insieme di curve di equazione cartesiana (x /a)^m + (y /b)^m = 1, con a, b > 0 e m ≠ 0, analizzate da G. Lamé che considerò il caso di m (indice o grado della curva) reale qualsiasi, non nullo. Se m è razionale la curva è algebrica; se è irrazionale la curva è trascendente. Per m = 2 la curva è un’ellisse; per m razionale e uguale alla frazione irriducibile p /q, si hanno nove casi diversi corrispondenti a diversi andamenti grafici, a seconda che p e q siano entrambi dispari o l’uno o l’altro sia pari (non possono essere entrambi pari altrimenti la frazione non sarebbe irriducibile) e che m sia minore di 0, compreso tra 0 e 1 oppure maggiore di 1 (nel caso m = 1 la curva si riduce a una retta). Le nove possibilità sono indicate in figura. Per m = 2/3 la curva è un asteroide.