Dalla prospettiva dei pittori alla prospettiva dei matematici

Dalla prospettiva dei pittori alla prospettiva dei matematici

Il progressivo abbandono nei dipinti su tavola dei fondi oro in favore di paesaggi e vedute urbane, l’attenzione al naturale scorrere delle luci e delle ombre proprie e portate nei volumi dei corpi e l’introduzione della prospettiva lineare nella pittura e nella scultura che si attuò nel corso del Quattrocento italiano costituiscono l’inizio di una nuova età della rappresentazione visiva che si irradiò dall’Italia verso il resto d’Europa.

Erwin Panofsky, in Die Perspektive als ‘symbolische Form’ (1927), sostenne che la prospettiva sarebbe stata inventata da Filippo Brunelleschi a Firenze intorno al 1420. Tale approccio, nel corso del secolo scorso, ha dato luogo a una sorta di narrazione epica del mutamento nei modi di rappresentazione visiva che, sebbene risulti superata dallo stato attuale della ricerca, resiste indisturbata nella divulgazione della storia dell’arte.

Alla luce degli studi più recenti si può affermare che la diffusione e il radicamento nella coscienza degli italiani di una nuova concezione della luce, intesa non più come ente metafisico ma come fenomeno fisico, diede l’avvio a una nuova età del pensiero estetico e scientifico. Tale nuova concezione della luce è il risultato della trasmissione di saperi scientifici, in particolare dell’ottica, dal mondo arabo all’Occidente latino, e della loro propagazione attraverso la mediazione degli ordini religiosi negli studi universitari e tra gli intellettuali umanisti. Infine, il diffondersi negli ambienti degli artisti di questa nuova concezione della luce, trasmessa dalla teoria della visione di Ibn al-Haytham, è, con ogni probabilità, all’origine della nuova attenzione per il valore della realtà e della natura che nella rappresentazione visiva si affermano a fianco dei valori simbolici.

La diffusione della teoria della visione di Ibn al-Haytham in Italia

Il trattato Kitāb al-Manāzir (Libro d’ottica), scritto tra il 1028 e il 1038 da Abū ‛Alī al-Ḥasan ibn al-Ḥasan ibn al-Haytham (965-1039/1040), noto nell’Occidente latino come Alhacen, e poi dal 17° sec. come Alhazen, giunse in Europa, sul finire del 12° sec., o al più tardi nella prima metà del 13°, e si diffuse, mancante dei primi tre capitoli del primo libro, con il titolo latino De aspectibus. I due centri universitari di Oxford e Parigi furono i luoghi dove la perspectiva del filosofo arabo fu elaborata come scienza cristiana, e la curia papale, nelle sedi di Roma e Viterbo, fu suo centro di diffusione nell’Italia centrale.

Il primo e principale promotore della ricezione della teoria della visione di Alhacen fu il francescano Ruggero Bacone (1214/1220-dopo il 1292), alla cui Perspectiva deve accostarsi anche la Perspectiva communis (1277-1279) di John Peckham (1230-1292), un trattato molto breve e sintetico, scritto come testo di riferimento per le lezioni che il filosofo tenne presso la curia romana. Nel 14° sec. il volumetto fu adottato come testo da diverse università europee, garantendo una diffusione standardizzata delle teorie del filosofo arabo negli ambienti intellettuali del continente per almeno tre secoli.

La Perspectiva (1270-1278), che Witelo (1220/1230-dopo il 1277) aveva scritto a sua volta su invito di Guglielmo di Moerbecke, consiste, invece, in una voluminosa parafrasi del De aspectibus, che collocò stabilmente la teoria ottica di Alhacen nell’alveo dei saperi geometrici e filosofici dell’Europa latina e cristiana.

La curia romana fu il centro di diffusione della nuova teoria della visione di Alhacen, mediata dai tre diversi approcci di Bacone, Peckham e Witelo. L’ipotesi che la diffusione del nuovo sapere scientifico possa aver orientato gli sviluppi dei metodi di rappresentazione dello spazio in pittura e scultura nell’Italia centrale nello scorcio del 13° sec. e nel 14° è fondata. Gli affreschi della Basilica superiore di San Francesco ad Assisi, in cui si manifesta il primo cambiamento in senso realistico nella rappresentazione pittorica, e che furono dipinti nei decenni immediatamente successivi alla diffusione dell’opera di Bacone e delle lezioni di Peckham nella curia papale, potrebbero essere il primo effetto della teoria della visione di Alhacen sulla rappresentazione pittorica.

La teoria della visione diretta di Alhacen fu promossa non solo dall’opera di mediazione degli ordini mendicanti e della curia romana, ma anche dalla presenza di testimoni manoscritti, come, per es., la traduzione in volgare del De aspectibus, oggi conservata presso la Biblioteca apostolica vaticana (codice Vat. lat. 4595), realizzata in Toscana tra la fine del 14°  e l’inizio del 15° secolo. Chi promosse e sostenne la traduzione dal latino al volgare del trattato di Alhacen aveva, verosimilmente, l’intenzione di renderlo disponibile direttamente a quegli operatori che non disponessero di sufficienti conoscenze di latino. Che la traduzione in volgare del De aspectibus fosse nota e disponibile agli artisti è provato nel caso di Lorenzo Ghiberti (1378-1455), che ne trascrisse interi passi nel Commentario terzo. La disponibilità del trattato di Alhacen presso gli artisti fiorentini del Quattrocento non può essere stata senza conseguenze per la trasformazione della rappresentazione pittorica in senso naturalistico avvenuta proprio in quegli anni.

La traduzione volgare del De aspectibus rendeva disponibile agli artisti fiorentini la più avanzata teoria della visione del tempo e le conoscenze più avanzate sul comportamento del colore al variare della luce e sulle ombre colorate. Insegnava come la vista, attraverso un termine di paragone (il corpo umano secondo Alhacen), misuri le distanze e le grandezze di una sequenza di corpi collocati in una disposizione ordinata e continuata. Rendeva inoltre utilizzabili, dagli operatori in grado di ripeterle, numerose esperienze di osservazione della formazione delle immagini su specchi piani, concavi e convessi, osservate attraverso piccoli fori praticati su tavolette di legno e di ottone.

In conclusione, la traduzione volgare del trattato di Alhacen rendeva disponibili agli artisti quelle conoscenze che sono i prerequisiti sia delle prime rappresentazioni pittoriche illusorie dello spazio tridimensionale in pittura e in scultura, sia dell’esperienza della prima tavoletta di Filippo Brunelleschi (1377-1446), sia della concezione della pittura come «intersegazione» della piramide, dichiarata da Leon Battista Alberti nel De pictura (1435).

La teoria della visione di Alhacen

La teoria della visione di Alhacen spiega la trasmissione all’organo del senso delle forme colore emesse dai corpi illuminati, applicando la geometria della piramide visiva alla teoria della propagazione della luce. Alhacen considerava i raggi visivi che formano la piramide della teoria estromissiva euclidea un modello puramente matematico e, dunque, integrabile alla sua teoria della visione. La traslazione della forma colore nell’occhio avviene dentro una piramide che ha la cuspide all’interno dell’occhio e la cui base è la superficie del corpo che emette luce propria o riflessa. La piramide di Alhacen non è visiva ma radiosa, cioè formata di raggi di luce, e figurata perché ciascun singolo raggio porta la forma colore di un punto del corpo che emette la luce stessa. La piramide radiosa e figurata, intersecando il glaciale (uno degli umori dell’occhio), riproduce punto per punto sulla superficie della sfera glaciale la forma colore emessa dal corpo visibile, che viene trasmessa al cervello. L’intelletto, con l’intervento della «virtus distinctiva», comprende nella forma colore trasmessa dalla piramide figurata le «intentiones», le caratteristiche visive, del corpo che emette la luce.

La «quantità della distanza»

Per Alhacen la caratteristica visiva della quantità della distanza è percepita dalla vista e compresa dall’intelletto solo per distanze che non eccedono la mediocrità, ovvero né troppo vicine né troppo lontane, ed è certificata solo quando nel campo visivo siano intergiacenti corpi noti che fungano da termini di paragone attraverso cui misurare la distanza.

Nella Perspectiva communis Peckham sintetizza la teoria di Alhacen della conoscenza della distanza mediante la sola vista in un paragrafo il cui titolo è Solo la distanza mediocre è certificabile, e ciò per mezzo di corpi intergiacenti disposti in modo continuo e ordinato (John Peckham and the science of optics, 1970, p. 140). Questa trattazione contiene in sintesi tutti gli elementi necessari: non tutto ciò che entra nel campo visivo è misurabile con la sola vista, ma solo ciò che si situa a una distanza moderata dall’occhio. Dei corpi e spazi che eccedono la mediocrità, posti troppo vicini o troppo lontani dall’occhio, l’intelletto percepisce le distanze, ma non stabilisce le quantità.

La comprensione della misura degli spazi e dei corpi mediante la sola vista è possibile solo per le distanze comprese tra un massimo e un minimo del campo visivo.

Ma cosa sono i «corpi intergiacenti disposti in modo continuo e ordinato»? Tali corpi sono cose già note all’osservatore (che ne conosce le dimensioni per esperienza pregressa), disposte in modo ordinato e costante nel suo campo visivo. Secondo Alhacen, l’osservatore riconosce corpi già noti, ne rammenta le dimensioni e di conseguenza misura lo spazio che essi occupano e, per comparazione, comprende sia la misura della distanza che corre tra i corpi, sia la distanza che lo separa dai corpi stessi, e questo, come si è detto, solo per distanze che non eccedono la mediocrità, cioè per corpi che non siano troppo lontani dall’osservatore o troppo vicini all’occhio.

Per un lettore attuale i termini latini «continuata et ordinata» usati da Peckham potrebbero essere attributi volti a specificare le modalità secondo le quali i corpi devono essere disposti nel campo visivo. Intesi in tale maniera, essi possono evocare le sequenze di colonne, pilastri e archi, le quinte di palazzi, i pavimenti a scacchiera e i soffitti a cassettoni che popolano, da Giotto in poi, la pittura italiana del Trecento e del Quattrocento.

Nondimeno, per Alhacen, Bacone, Witelo, Peckham e per i loro lettori, i termini «continuata et ordinata» potevano rivestirsi di un preciso significato matematico, per noi non più evidente.

Nella tradizione latina medievale del libro V degli Elementi di Euclide due definizioni portano i nomi di ordinata e continua. Esse sono tramandate ciascuna in una traduzione diversa degli Elementi di Euclide, non compaiono mai insieme nella stessa versione del trattato e non si trovano nella tradizione testuale degli Elementi stabilita da Johan L. Heiberg nel 19° sec.; non leggendosi nelle edizioni moderne del trattato esse sono semplicemente cadute nell’oblio. Tuttavia, erano note ai dottori in «perspectiva» della fine del 13° sec., e lo erano ancora agli studiosi di Euclide del 17° sec. come Galileo Galilei.

La «proporzione ordinata» è tramandata solo dalla traduzione degli Elementi di Gherardo da Cremona (1114-1187), nella quale è riportata come XIX definizione. La «proporzionalità continua» è presente invece solo nella tradizione di Adelardo da Bath (1070-1160) come V definizione. La «proporzione ordinata» di Gherardo da Cremona consiste in due serie di grandezze in cui i termini di ciascuna serie sono in proporzione secondo un rapporto identico: date le due serie di grandezze « A. B. C. » e « D. E. F. », A sta a B come D sta a E ; così B sta a C come E sta a F. Come una simile proporzione potrebbe descrivere lo spazio in una rappresentazione pittorica?

Si consideri il caso del colonnato di un chiostro: le altezze apparenti delle colonne e le distanze apparenti tra le coppie di colonne mantengono relativamente sempre lo stesso rapporto e sono dunque in proporzione ordinata.

La «proporzione continua» per Campano da Novara (m. 1296), il cui commento ha costituito per lungo tempo lo standard interpretativo, consiste invece non in una proporzione, ovvero in un rapporto tra due grandezze, ma in una proporzionalità, cioè in una similitudine di proporzioni formata almeno da tre termini dello stesso genere che può essere scritta nella forma A:B=B:C.

La proporzionalità continua è senz’altro appropriata a descrivere le grandezze apparenti che diminuiscono in prospettiva, come, per es., le altezze dei personaggi o delle colonne e la profondità delle mattonelle dei pavimenti o dei cassettoni dei soffitti. La proporzione ordinata può descrivere il rapporto tra le altezze e le larghezze relative della composizione pittorica, per es. l’altezza dell’uomo e la larghezza del pavimento; con l’uso della proporzionalità continua è possibile descrivere la diminuzione apparente delle grandezze nella profondità dello spazio pittorico, per es. la diminuzione in profondità delle mattonelle di un pavimento.

Filippo Brunelleschi perspettivo ingegnoso

Nel 1413 il poeta Domenico da Prato definì Brunelleschi «prespettivo [sic] e ingegnoso uomo» (Brunelleschi: l’uomo e l’artista, a cura di P. Benigni, 1977, p. 97). Si deve notare che in quell’anno il termine indicava senza dubbio la filosofia della visione, non la prospettiva lineare, perché quest’ultimo significato era ancora di là da venire. Due notizie relative a Brunelleschi come colui che trovò la prospettiva dei pittori si leggono nel trattato di architettura di Antonio Averulino detto il Filarete (1400 ca.-1469): ambedue le citazioni associano l’invenzione della prospettiva allo specchio. In particolare la prima menzione si trova subito dopo la presentazione di un metodo grafico per realizzare lo scorcio di un pavimento, che Filarete cita, quasi parola per parola, dal De pictura di Alberti.

Stando a Filarete, Brunelleschi avrebbe trovato un modo per disegnare un piano (un pavimento o un soffitto) in scorcio, osservando negli specchi il comportamento delle linee ortogonali e parallele al piano di osservazione e delle diminuzioni che si verificano nelle distanze relative. Filarete non spiega, però, come guardando in uno specchio si possa mettere a punto la procedura grafica che ha appena illustrato, anche se dimostra di essere cosciente che la questione non è semplice. Infatti se ci si pone davanti a uno specchio, siamo noi stessi a essere riflessi e non le cose che vorremmo disegnare; queste possono essere viste solo se l’osservatore è spostato da un lato rispetto allo specchio, e dunque solo mediante un angolo di riflessione che non sia retto.

Un’altra citazione di Brunelleschi come inventore della prospettiva è in relazione con gli specchi piani. Si tratta del famoso brano della Vita di Filippo Brunelleschi scritta da Antonio di Tuccio Manetti (1423-1497) quarant’anni dopo la morte di Brunelleschi, in cui si descrivono due tavolette dipinte con prospettive, oggi perdute.

Dalle due tavolette, secondo il biografo, sarebbe derivata una regola che era alla base delle rappresentazioni prospettiche realizzate intorno al 1480. Manetti non dice quale sia la regola, ma riferisce che il dipinto del Battistero di San Giovanni era «fatto con tanta diligenza e gentilezza, e tanto co’ i colori de marmi bianchi e neri, che non è miniatore che lo avessi fatto meglio» (Vita di Filippo Brunelleschi, a cura di D. De Robertis, 1976, p. 59), senza fare menzione di alcuna procedura grafica di tipo prospettico.

Manetti attribuisce a Brunelleschi il primato nell’aver trovato la maniera di rappresentare proporzionatamente in pittura le diminuzioni degli spazi e degli oggetti in funzione della distanza da cui si guardano, trovando così la regola della prospettiva dei pittori. Precisando che tale modo di rappresentare la diminuzione delle grandezze apparenti che costituisce la «prospettiva dei pittori» è una parte della «perspectiva» intesa come scienza ottica.

Sulle due tavolette perdute si è scritto molto; tuttavia, le interpretazioni del dispositivo ottico descritto da Manetti, elaborate al fine di comprendere quale fosse «la prospettiva di Brunelleschi», tentate da numerosi storici dell’arte sono spesso andate al di là di quanto fosse possibile sostenere in termini logici, storici e scientifici. Nondimeno, dalla descrizione delle tavolette si possono comunque inferire ipotesi sulle conoscenze di teoria della visione di Brunelleschi per comprendere a quali parti della teoria ottica l’architetto fiorentino abbia prestato maggiore attenzione.

Brunelleschi e la teoria della visione

Filarete e Manetti asseriscono che Brunelleschi fece uso degli specchi per trovare la ragione della diminuzione delle grandezze apparenti. Per Filarete, Brunelleschi osservò «dirimpetto all’occhio» (Trattato di architettura, a cura di A.M. Finoli, L. Grassi, 1972, p. 653) nello specchio le apparenze di immagini reali riflesse per ricavarne un metodo per rappresentarle graficamente e pittoricamente. L’esperienza della prima tavoletta prevedeva che l’osservatore: «con l’una mano s’accostassi allo occhio [la tavoletta dipinta] e nell’altra tenessi uno specchio piano al dirimpetto, che vi si veniva dentro a specchiare la dipintura» (Vita di Filippo Brunelleschi, cit., p. 55, corsivo mio). E dunque essa consiste proprio nel guardare frontalmente in uno specchio, senza esservi riflesso, l’oggetto dipinto.

Il Brunelleschi «perspectivo e ingegnoso uomo» doveva aver conoscenza della catottrica, la parte della teoria della visione che indaga la formazione delle immagini negli specchi. Non è indispensabile ipotizzare che egli lavorasse con la supervisione di un dotto, dal momento che per poter dominare la catottrica la conoscenza del latino è necessaria ma non sufficiente, serve a poco se non si è in grado di comprendere i complessi diagrammi che accompagnano il testo. Un architetto del livello di Brunelleschi avrebbe potuto invece non solo comprenderli, ma anche disegnarli con la dovuta chiarezza e precisione e, con l’aiuto della traduzione volgare del De aspectibus di Alhacen, avrebbe potuto intraprendere le sue indagini sulla formazione delle immagini negli specchi piani, senza dover chiedere aiuti per la lettura del trattato.

La prima esperienza raccontata da Manetti, quella della cosiddetta prima tavoletta, parrebbe rientrare a pieno titolo nell’ambito della catottrica. Osservare uno specchio attraverso un foro è un metodo di indagine esperito da Alhacen. L’osservazione attraverso un singolo foro aveva lo scopo di selezionare il solo raggio riflesso passante per il centro dell’occhio, l’asse visivo, o, come lo avrebbe chiamato Alberti, il «raggio centrico». Il quale, considerato nei termini geometrici della piramide visiva, è l’unico che cada perpendicolarmente sulla superficie dello specchio.

Leon Battista Alberti: la pittura come intersecazione della piramide visiva

La famosa metafora della «pittura come finestra aperta» che Alberti ideò nel De pictura sottintende la «intersecazione» della piramide visiva. Tale concetto non esiste né nella teoria ottica di Euclide, né in quella di Tolomeo. L’idea che un’immagine si formi, nell’occhio, nello specchio o in un corpo diafano di densità diversa dall’aria (come un vaso di cristallo colmo d’acqua), mediante l’intersecazione della piramide visiva fu elaborata per la prima volta da Alhacen e si diffuse in Italia attraverso le traduzioni della sua opera e i commentari che ne scaturirono.

Alberti applica il concetto di «intersecazione della piramide visiva» alla pittura in due luoghi del De pictura: nel libro I, quando formula la metafora della pittura come «vetro tralucente», e nel libro II, quando introduce il «velo», uno strumento di «non picciola commodità», consistente in un «tessuto rado» posto «tra l’occhio e la cosa veduta» in modo che la piramide visiva penetri «la rarità del velo» (De pictura (redazione volgare), a cura di L. Bertolini, 2011, p. 261). Il velo e il vetro servono ad Alberti per dimostrare operativamente l’innovativo modo di intendere la pittura come un piano che interseca la piramide radiosa emanata dai corpi illuminati. Se quella del vetro è una metafora ispirata dagli studi di Alhacen sulla rifrazione, il velo, invece, è uno strumento, di cui Alberti rivendica la paternità, che dovrebbe servire al pittore per ritrarre le figure di piccole dimensioni, tra cui anche la figura umana. L’esperienza del velo albertiano fu ripresa da Leonardo da Vinci con alcune varianti notevoli, e poi da Albrecht Dürer (1471-1528), che mise a punto due strumenti prospettografi da cui discendono quelli di Ludovico Cardi detto il Cigoli (1559-1613).

Secondo Alberti, il velo non è adatto a ritrarre tutti i corpi visibili. Egli infatti afferma: «alle superficie maggiori [le architetture] ci convien trovare nuove ragioni» (De pictura, cit., p. 264), ovvero, una ratio che consenta di stabilire mediante un metodo prospettico una proporzione tra la figura umana e le architetture, che sia valida in tutto il piano pittorico; in altre parole, determinare nella rappresentazione pittorica una corretta proporzione tra figura umana e architettura.

L’altezza del «dipinto uomo» nel «modo ottimo» – così Alberti chiama il suo metodo prospettico – è il termine noto di comparazione di tutti i corpi rappresentati nella pittura e rappresenta l’unità di misura degli edifici e delle distanze. La dimensione del corpo umano secondo Alhacen è l’unità di misura che attraverso l’esperienza assicura il metro di giudizio per valutare le distanze e le quantità. Al tempo in cui Alberti scrive, le membra umane fornivano ancora i nomi di unità di misura più comuni: palmo, piede e braccio. L’osservatore, con la sua personale conoscenza pregressa, usando la figura umana dipinta come termine di comparazione, valuta i rapporti proporzionali e compositivi del dipinto.

Alberti stabilisce un rapporto tra l’altezza dell’uomo dipinto e la fila di mattonelle su cui poggia, che si mantiene costante in tutto il piano del pavimento: l’altezza dell’uomo dipinto è sempre pari alla larghezza di tre delle mattonelle su cui poggia i suoi piedi. Dunque, in ogni punto del pavimento altezze e ampiezze sono sempre coordinate da una stessa proporzione e le cose rappresentate mantengono in ogni punto gli stessi rapporti tra altezza e larghezza.

Questo tipo di rapporto, come abbiamo visto, si trova descritto con il nome di «proporzione ordinata» nella traduzione degli Elementi di Euclide di Gherardo da Cremona.

Alberti, prima di presentare il suo «modo ottimo», illustra un metodo usato da «alcuni», che l’umanista non identifica meglio, i quali per mettere in proporzione la diminuzione degli intervalli tra le linee parallele del pavimento, procedono stabilendo a piacere la distanza dalla base della prima linea. La distanza tra la prima e la seconda linea la trovano dividendo in tre la prima quantità e prendendone due parti, la quantità tra la seconda e la terza allo stesso modo e così via.

Alberti considera errato questo metodo perché la prima linea è posta a caso. Che le grandezze recedendo in profondità diminuiscano di un terzo, cosa che ai nostri occhi pare un espediente puramente empirico, non procura all’umanista nessun disagio. Anzi, per lui è accettabile, perché «gli spazi successivi seguono a ragione», cioè secondo una proporzione che, asserisce l’umanista, i matematici chiamano superbipartiente. Nel rapporto matematico implicito in questo modo di diminuire le grandezze possiamo riconoscere la proporzionalità continua descritta nella traduzione degli Elementi commentata da Campano da Novara.

Per individuare la proporzione continua che descrive la diminuzione delle grandezze apparenti delle mattonelle – la quale costituisce il vero problema matematico della rappresentazione prospettica –, Alberti illustra un metodo basato sull’intersecazione della piramide visiva e sulla proporzionalità dei triangoli simili. Il «modo ottimo» introduce, dunque, un cambiamento di paradigma nella rappresentazione visiva della diminuzione delle quantità, che sono rappresentate mediante la geometria dei triangoli della visione in funzione della distanza tra osservatore e intersecazione della piramide visiva e non più mediante una proporzione numerica, sia pure descritta nella tradizione medievale degli Elementi di Euclide. Per questa ragione, il «modo ottimo» costituisce la prima testimonianza scritta di quello che oggi chiamiamo prospettiva. Nondimeno il «modo ottimo» non è la prospettiva, almeno come la intendiamo noi oggi. Alberti, infatti, continua a mettere in rapporto le altezze e le larghezze con la proporzione ordinata, e stabilisce la diminuzione delle grandezze apparenti solo in funzione della distanza da cui si osserva la pittura: «poi constituisco quanto io voglia distanza dall’occhio alla pittura» (De pictura, cit., p. 240) è chiaramente detto nella redazione volgare. Ciò non è senza conseguenze per la rappresentazione e, con il senno del poi, possiamo anche dire che dal punto di vista della prospettiva lineare si tratta di un errore.

Piero della Francesca: la proporzione degradata

Piero della Francesca (1412 ca.-1492) finì di scrivere il De prospectiva pingendi negli anni Settanta del Quattrocento. Nel libro I, a metà del teorema XI, prima di entrare nel merito della procedura prospettica, Piero avvia una digressione, illuminante per comprendere il dibattito in corso sulla natura della proporzione prospettica, il cui fine è liberare il campo dalle possibili obiezioni dei sostenitori delle proporzioni numeriche, introducendo il concetto che la riduzione delle grandezze apparenti si trova mediante una proporzione che ha per termini la distanza tra l’occhio e il piano d’intersezione della piramide visiva e la distanza tra il detto piano e la cosa veduta.

Dunque, quarant’anni dopo il De pictura, il metodo della proporzionalità continua, finalizzato a determinare la diminuzione delle grandezze apparenti, era forte, al punto che Piero ritenne necessario avvertire «in premessa» che la proporzione appropriata per descrivere la riduzione delle grandezze apparenti non è una proporzione contemplata nella tradizione medievale degli Elementi di Euclide, ma è una proporzione basata sulla geometria della piramide visiva, che Piero denomina proporzione degradata.

Piero della Francesca superò anche l’errore commesso da Alberti nello stabilire la distanza su cui basare la diminuzione delle grandezze apparenti. Il pittore e matematico ha ben chiaro che se la perpendicolare che rappresenta il quadro che interseca la piramide visiva cambia posizione, e dunque mutano le distanze tra l’occhio e il quadro e tra il quadro e la cosa veduta, pur rimanendo la distanza tra l’occhio e la cosa veduta immutata, la proporzione con cui diminuiscono le grandezze apparenti cambia. Piero dimostra così che la diminuzione delle grandezze apparenti non è determinata né da una proporzione di quelle descritte nel libro V degli Elementi, né dalla distanza che separa il piano di rappresentazione dall’occhio, come asserì Alberti, ma è regolata dalla proporzione che tali grandezze hanno sia con la distanza tra l’occhio e il piano d’intersezione, sia con la distanza tra il piano di intersezione e la cosa veduta.

Si tratta di un problema matematico che per la teoria delle proporzioni del Quattrocento non aveva soluzioni e che Piero della Francesca risolse mediante la geometria dei triangoli proporzionali.

La soluzione geometrica del problema della rappresentazione della diminuzione delle grandezze apparenti aprì una nuova fase della storia della prospettiva, che d’ora in poi si caratterizza sempre di più come una disciplina fondata sulla geometria euclidea e dimostrata mediante il disegno lineare, pronta per passare dal dominio disciplinare dei pittori a quello degli architetti.

fig. 1

fig. 2

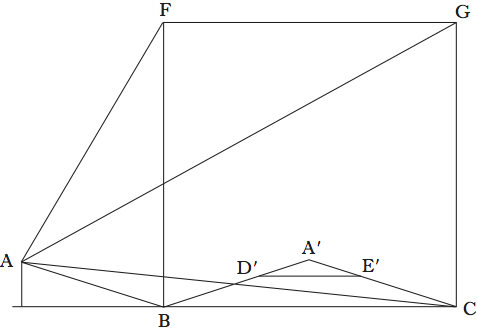
Piero della Francesca nel De prospectiva (libro I, capp. XIII e XXIII) illustrò due regole generali. In estrema sintesi la prima regola deriva, correggendolo, dal «modo ottimo», e interseca sulla verticale del quadrato BCGF che contiene il quadrilatero da mettere in prospettiva (fig. 1). In questa prima regola ancora si riconosce il sistema occhio-piano di intersezione-corpo visibile. La seconda regola non ha precedenti ed è uno sviluppo in senso geometrico della procedura prospettica che rende speditivo il metodo. In essa Piero della Francesca elimina il piano perpendicolare di intersezione e trova lo scorcio del quadrangolo BCE′D′ intersecando sulla congiungente il piano di terra BC e il punto dell’occhio A (fig. 2).

Queste due regole nel corso del Cinquecento vengono riprese nei trattati di diversi architetti che avviarono un processo di standardizzazione delle procedure grafiche, dando luogo a quella tradizione operativa che venne chiamata la «prospettiva pratica». Il matematico Egnatio Danti (1536-1586), nel commento a Le due regole della prospettiva pratica di Jacopo Barozzi da Vignola (1507-1573), abbozzò una sorta di genealogia della cosiddetta «regola degli antichi»: «Piero della Francesca fu il primo che ne scrisse, Francesco di Giorgio la tramandò a Baldassarre Peruzzi che la insegnò a Serlio» (Le due regole della prospettiva pratica di M. Iacomo Barozzi da Vignola, 1583, p. 82), il quale, aggiungiamo noi, la trasmise a Vignola. La genealogia elaborata da Egnatio Danti è abbastanza plausibile e indica che lo sviluppo della teoria prospettica nel Cinquecento si svolse tra Borgo San Sepolcro, Urbino e Siena. Tuttavia anche l’architetto urbinate Bramante (1444-1514) potrebbe essere il tramite con Piero della Francesca e Baldassarre Peruzzi (1481-536). D’altra parte la questione non va impostata nei termini di una genealogia, ma piuttosto nell’individuazione del contesto in cui le regole della prospettiva di Piero della Francesca divennero importanti per gli architetti.

Il grande cantiere di San Pietro a Roma, dove i quesiti sulla rappresentazione architettonica furono al centro del dibattito e della sperimentazione, e dove la presenza di personalità dell’ambiente urbinate, in grado di conoscere e sperimentare il trattato di Piero, fu consistente, potrebbe costituire il contesto operativo in cui la cristallina perizia grafica e la valida teoria geometrica del maestro di Borgo erano ammirate e studiate. Le sue rappresentazioni prospettiche e proiezioni ortogonali dei corpi regolari vi dovevano essere studiate per trarne modelli e spunti per la soluzione di problemi di rappresentazione dell’architettura.

Vignola, già nel 1559, aveva scritto le sue regole della prospettiva pratica: se ne ha notizia dalle carte dell’architetto conservate presso l’Accademia nazionale di San Luca di Roma.

Le due regole della prospettiva pratica di Vignola sono esplicitamente rivolte a «pittori e disegnatori» e sono pensate per un lettore esperto, capace di decifrare i diagrammi, per un «operatore» che sappia ripetere autonomamente i disegni e «operando conoscere». Non si coglie alcun senso di inferiorità nei confronti della geometria, rispetto alla quale la prospettiva è «scienza subalternata», ma una grande fiducia nel disegno tecnico come linguaggio attraverso il quale la geometria si esprime pienamente.

Il cap. III della seconda regola è cruciale per lo sviluppo della teoria proiettiva, poiché introduce il concetto di concorrenza delle parallele in un punto sulla linea d’orizzonte. Scrive Vignola:

Se bene secondo la Geometria le linee parallele non si possono mai toccare, o vero unirsi insieme dalli capi, ancor che vadino all’infinito; ma tirate in prospettiva fanno altro effetto percioché si vanno ad unire all’orizonte in un punto più o meno discosto l’uno dall’altro secondo che sarà la positura delle linee (Le due regole della prospettiva pratica, cit., p. 101).

Vignola con questa sintesi teorica avvia un nuovo modo di pensare lo spazio prospettico, la cui potenzialità sarà compresa e sviluppata appieno da Guidobaldo Dal Monte (1545-1607).

La prospettiva dei matematici

Egnazio Danti nel suo commento ricorda più volte che il trattato di prospettiva fu elaborato da Vignola con un lungo lavoro di revisioni, anche sostanziali, del testo. Tale lavoro di stesure e redazioni si svolse in un periodo di tempo in cui Vignola era al servizio della corte Farnese. Negli stessi anni erano al servizio dei Farnese Federico Commandino (1506-1575), matematico presso la corte del cardinal Ranuccio a Roma, e Giovan Battista Benedetti (1530-1590), matematico presso la corte del duca Ottavio a Parma. I contatti diretti e certi con Commandino e quelli intuibili con Benedetti, che è bene ricordarlo sono fra i massimi matematici di quegli anni, sono indicativi del contesto intellettuale in cui è maturata la teoria prospettica di Jacopo Barozzi.

I rapporti tra Barozzi e Commandino sembrano essere stati reciprocamente utili, anche se non privi di toni polemici. Negli anni dell’elaborazione del trattato di prospettiva Barozzi era al servizio del cardinale Ranuccio Farnese, alla cui corte l’architetto e il matematico ebbero modo di incontrarsi. Federico non fa mistero di conoscere Barozzi: nella dedicatoria del suo Planisphaerium Ptolemaei commentarius, edito a Venezia nel 1558, Commandino definisce Barozzi: «architetto eccellente e assai competente [che] conosce così bene la prospettiva che in questa parte di scienza non cede, senza dubbio, il campo a nessuno del nostro tempo» (La prospettiva di Federico Commandino, a cura di R. Sinisgalli, 1993, p. 58).

Il commentario di Commandino a Tolomeo consiste in un vero trattato di prospettiva. Egli decise di redigerlo in tale forma perché, scrive il matematico,

il Planisferio di Tolomeo non poteva essere capito se non a stento e con grande fatica […]. L’ho letto tutto con estrema cura e mi sembra, ma potrei sbagliarmi, di averlo capito chiaramente, riguarda quella parte dell’ottica che gli antichi chiamarono scenografia. […]. Ai nostri giorni, presso pittori e architetti tutt’altro che spregevoli, si tramanda un certo modo di operare che a me è stato di grandissimo aiuto nel seguire il pensiero di questo piccolo libro» (La prospettiva di Federico Commandino, cit., p. 57).

Poche righe più in basso si trova quell’elogio di Vignola prospettico che abbiamo già ricordato.

Quello che ci interessa di più in questa lettera dedicatoria è che Commandino dichiara, neanche troppo implicitamente, di essersi servito del consiglio di architetti e pittori suoi contemporanei per ripristinare il senso di un testo scientifico, il Planisferio, corrotto dalle molteplici traduzioni e trascrizioni. Vignola fu con ogni probabilità consultato da Commandino. Quale potesse essere stato il «modo di operare» così utile al matematico è suggerito dalla presenza tra le sue carte, conservate presso la Biblioteca universitaria di Urbino, dello schizzo di una procedura prospettica che, senza dubbio alcuno, descrive il cap. V della Prima regola di Vignola. In questo contesto, «modo di operare» significa operare graficamente, cioè il modo di rappresentare graficamente i problemi geometrici enucleati nel testo corrotto del trattato, che non potevano essere sciolti che attraverso la loro restituzione grafica. Se ne evince che il disegno fu usato come linguaggio per interpretare, e in un certo senso come uno strumento per «restaurare» le conoscenze tolemaiche.

Vignola, come abbiamo visto, si espresse a favore di una molteplicità di regole nella prospettiva che portano tutte allo stesso risultato. Giovan Battista Benedetti nel De rationibus operationum perspectivae, pubblicato nel Diversarum speculationum mathematicarum et physicarum liber (1585), asserì la verità di una sola regola prospettica. Benedetti da scienziato preferiva la prima regola, quella in cui il metodo dell’intersezione della piramide visiva, direttamente derivato dalla teoria della visione, è riconoscibile nella procedura grafica.

Nel 1600, l’allievo di Commandino, Guidobaldo Dal Monte, pubblicò i Perspectivae libri sex. Il trattato, corredato da numerose tavole disegnate, è scritto in latino e dunque non si rivolge più ad artisti e professionisti ma ai dotti. Nella sua opera Guidobaldo riprende proposizioni e diagrammi del trattato di Vignola, senza riconoscerne il debito, ma soprattutto fa sua l’idea di Vignola, già ripresa e commentata da Danti, che le parallele in prospettiva si incontrano in un punto sulla linea d’orizzonte. Guidobaldo ha il merito di averla sviluppata nel concetto di punto di concorrenza all’infinito delle parallele, che segnò l’ingresso della prospettiva nel dominio disciplinare dei matematici e pose le basi teoriche di quella che sarà la geometria descrittiva.

Opere

Opticae thesaurus Alhazeni arabis libri septem nuncprimum editi. Eiusdem liber De crepuscoli et nubium ascensionibus. Item Vitellionis Thuringopoloni libri X, ed. F. Risner, Basel 1572; ed. D. Lindberg, New York-London 1972.

Io. Baptistae Benedicti Patritii Veneti Diversarum speculationum mathematicarum & physicarum liber, Taurini 1585.

The opus majus of Roger Bacon, ed. R. Belle Burke, New York 1962.

John Peckham and the science of optics. Perspectiva communis, ed. D.C. Lindberg, Madison-Milwaukee-London 1970.

A. Averlino detto il Filarete, Trattato di architettura, a cura di A.M. Finoli, L.Grassi, introduzione e note di L. Grassi, Milano 1972.

Le due regole della prospettiva pratica di M. Iacomo Barozzi da Vignola, riprod. facs. dell’ed. Roma 1583, Vignola 1974.

A. Manetti, Vita di Filippo Brunelleschi, preceduta da La novella del grasso legnaiolo, a cura di D. De Robertis, con introduzione e note di G. Tanturli, Milano 1976.

Piero della Francesca, De prospectiva pingendi, a cura di G. Nicco-Fasola, Firenze 1984.

I sei libri della prospettiva di Guidobaldo dei marchesi Del Monte, a cura di R. Sinisgalli, Roma 1984.

The Latin translation of the Arabic version of Euclid’s Elements commonly ascribed to Gerard of Cremona, ed. H.L.L. Busard, Leiden 1984.

The optics of Ibn al-Haytham, Books 1-3 on Direct vision, ed. A.I. Sabra, 2 voll., London 1989.

La prospettiva di Federico Commandino, a cura di R. Sinisgalli, Firenze 1993.

Roger Bacon and the origins of perspectiva in the Middle Ages, critical edition and English translation of Bacon’s Perspectiva, introduction and notes by D.C. Lindberg, Oxford 1996.

L. Ghiberti, I Commentarii (Biblioteca nazionale centrale di Firenze, II, I, 333), a cura di L. Bartoli, Firenze 1998.

A. Mark Smith, Alhacen’s theory of visual perception, critical ed. with English translation and commentary of the first three books of Alhacen’s De Aspectibus, the medieval Latin version of Ibn al-Haytam, Kitab al Manāzir, Philadelphia 2001.

H.L.L. Busard, Campanus of Novara and Euclid’s Elements, 2 voll., Stuttgard 2005.

L.B. Alberti, De Pictura (redazione volgare), a cura di L. Bertolini, Firenze 2011.

Bibliografia

E. Panofsky, Die Perspektive als ‘symbolische Form’, «Vorträge der Bibliothek Warburg 1924-25», hrsg. F. Saxl, 1927 (trad. it. La prospettiva come forma simbolica e altri scritti, a cura di G.D. Neri, con una nota di M. Dalai, Milano 1961).

R. Wittkower, Architectural principles in the age of Humanism, London 1962 (trad. it. I principi architettonici dell’Umanesimo, Torino 1964).

M. Baxandall, Painting and experience in fifteenth century Italy, Oxford 1972 (trad. it. Pittura ed esperienze sociali nell’Italia del Quattrocento, Torino 1978).

D. Lindberg, Theories of vision from Al-Kindi to Kepler, Chicago-London 1976.

M. Kemp, Science, non-science, and nonsense. The interpretation of Brunelleschi’s perspective, «Art history», 1978, 2, pp. 134-61.

G. Saccaro Battisti, Alcuni esempi di omologia di strutture matematico-geometriche e di strutture logico ontologiche nella filosofia medievale come premesse alla prospettiva, in La prospettiva rinascimentale. Codificazioni e trasgressioni, Atti del Convegno internazionale, Milano (11-15 ottobre 1977), a cura di M. Dalai Emiliani, Firenze 1980, pp. 375-402.

E. Giusti, Euclides reformatus. La teoria delle proporzioni nella scuola galileiana, Torino 1993.

J. Elkins, The poetics of perspective, Ithaca 1994.

J. V. Field, Mathematics and art in the Renaissance, Oxford 1997.

G. Federici Vescovini, Alhazen vulgarisé. Le De li aspecti d’un manuscrit du Vatican (moitié du XIV^e siècle) et le troisième Commentaire sur l’optique de Lorenzo Ghiberti, «Arabic sciences and philosophy», 1998, 1, pp. 67-96.

D. Raynaud, L’hypothèse d’Oxford. Essai sur les origines de la perspective, Paris 1998.

Ch. Thoenes, P. Roccasecca, Vignola teorico, in Jacopo Barozzi da Vignola, a cura di R.J. Tuttle, B. Adorni, C.L. Frommel, C. Thoenes, Milano 2002, pp. 91-99.

J.V. Field, Piero della Francesca a mathematician’s art, New Haven 2005.

P. Roccasecca, Sebastiano Serlio: placing perspective at the service of architects, in Perspective, projections and design, technologies of architectural representation, ed. M. Carpo, F. Lemerle, London-New York 2008.

P. Roccasecca, Dalla prospettiva pratica alla prospettiva matematica, in Ars, techné, technica. A fundamentaçao teórica e cultural da perspectiva, a cura di M. Moraes Mello, Belo Horizonte 2009.

P. Roccasecca, La prospettiva lineare nel Quattrocento: dalle proporzioni continuata e ordinata alla proporzione degradata, in Proportions. Science, musique, peinture & architecture, ed. S. Rommevaux, Ph. Vendrix, V. Zara, Turnout 2011, p. 277-97.