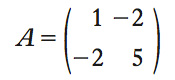positivo, definito
positivo, definito
Proprietà di una matrice quadrata (➔ matrice), che generalizza il concetto di positività di un numero scalare (➔ scalare). Consideriamo la definizione per una matrice quadrata a numeri reali. Una matrice quadrata A di dimensione m è definita p. se per ogni vettore colonna x non nullo, si ha x′Ax>0 dove x′ denota la trasposta di x (➔ vettore). L’espressione x′Ax>0 è chiamata forma quadratica ed equivale a x′Ax=Σijxiaijxj>0 dove aij è l’elemento (i,j)-esimo della matrice A, mentre x=(x1,...xm). ● La matrice A si dice semidefinita p. se, per ogni vettore colonna x non nullo, si ha x′Ax≥0. La matrice A è definita negativa se, per ogni vettore colonna x non nullo, si ha x′Ax<0, quindi anche se −A è definita negativa. Analogamente, una matrice A è semidefinita negativa se la matrice −A è semidefinita positiva (➔ anche negativo, definito). ● Una matrice è definita p. se e solo se i suoi autovalori sono tutti positivi (➔ autovettore). In particolare, una matrice diagonale è definita p. se e solo se tutti i suoi elementi sulla diagonale sono strettamente positivi. Come conseguenza, il determinante (➔) di una matrice definita p. è sempre p. (➔ matrice). Per es., la matrice
è definita p.: infatti, dato un qualsiasi vettore
x1=(x1,x2), si ha
x′Ax=x21−2x1x2−2x2x1+5x22=(x1−2x2)2+x22≥0,
si ha l’uguaglianza se e solo se x1=x2=0. L’hessiano (➔) di una funzione concava è definito negativo. La matrice di covarianze di un vettore aleatorio X=(X1,...,Xm) è invece definita p. (➔ covarianza). È vero anche il viceversa: ogni matrice definita p. è la matrice di covarianza di una distribuzione di probabilità multivariata (➔ distribuzione di probabilità).