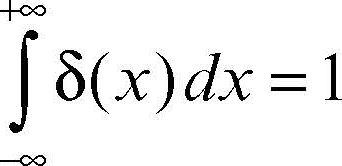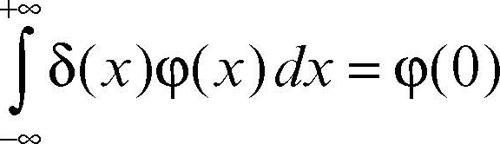Dirac, delta di

Dirac, delta di

Dirac, delta di distribuzione descrivibile informalmente come una “funzione” δ(x) che ha valore 0 per ogni x ≠ 0, mentre per x = 0 ha un valore infinito in modo che il suo integrale, calcolato sull’intervallo di tutti i possibili valori di x (asse reale) è uguale a 1:

Al di là dell’interpretazione euristica, formalmente il delta di Dirac non è una funzione, perché l’integrale tra −∞ e +∞ di una funzione ovunque nulla tranne in un punto è nullo. Essendo più propriamente una distribuzione, appartiene alla classe delle cosiddette funzioni generalizzate ed è l’applicazione che associa a ogni funzione φ regolare e nulla fuori da un chiuso e limitato (cioè a supporto compatto) il valore da essa assunto nell’origine (o in un determinato punto). Formalmente, quindi, si ha: <δ,> φ> = φ(0); dove la notazione < …, … > (crochet) è utilizzata per la valutazione di una distribuzione. È tradizione scrivere il crochet mediante un integrale che va del resto inteso nel senso precedente:

Poiché per alcuni scopi la distribuzione delta di Dirac può essere manipolata come una funzione, si parla a volte di funzione di Dirac o soprattutto di funzione impulsiva.