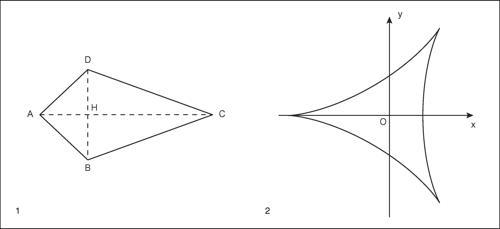
deltoide

Enciclopedia della Matematica (2013)

deltoide


deltoide o aquilone, quadrilatero avente un asse di simmetria passante per due suoi vertici opposti. Esso ha, quindi, due coppie di lati consecutivi di uguale lunghezza e gli angoli opposti di uguale ampiezza. Le diagonali di un deltoide sono perpendicolari e una delle diagonali è bisecata dallʼaltra. Indicate con d1 e d2 le misure delle diagonali, lʼarea del deltoide è:

formula

Caso particolare di deltoide è il rombo, nel quale tutti i lati hanno uguale lunghezza e gli assi di simmetria sono due, tra loro perpendicolari. Il termine è utilizzato anche per indicare una curva piana. La deltoide è una curva ipocicloide, detta ipocicloide di Steiner, chiusa e dotata di tre cuspidi.

DELTOIDE

Vedi anche
figura simmètrica In geometria, si dice simmetrica (centralmente, assialmente o rispetto a un piano) una figura che corrisponde a sé stessa in una simmetria. Per es. il triangolo equilatero è una f.s. assialmente rispetto a tre assi, mentre il cerchio è una f.s. centralmente e rispetto ai suoi infiniti diametri. perpendicolarità In geometria piana, relazione che sussiste tra rette che intersecandosi formano quattro angoli uguali. Nello spazio, la relazione di p. sussiste tra due piani se essi si intersecano formando quattro diedri uguali; si parla di p. anche tra due rette sghembe se l'una è parallela a una retta complanare ...
Tag
Altri risultati per deltoide
  • deltoide
    Enciclopedia on line
    Anatomia Il muscolo più superficiale e più voluminoso della spalla: ricopre l’articolazione scapolo-omerale e dà alla spalla la forma rotondeggiante. Esercita azione abducente ed elevatrice del braccio. Matematica In geometria, figura formata da due triangoli isosceli aventi la base in comune e altezze ...
Vocabolario
deltòide
deltoide deltòide agg. e s. m. [dal gr. δελτοειδής, comp. di δέλτα, nome della lettera Δ, e -ειδής «-oide»]. – 1. A forma di delta maiuscolo. In anatomia, muscolo d. (e più spesso il deltoide s. m.), il muscolo più superficiale e più voluminoso...
deltòide-dodecaèdro
deltoide-dodecaedro deltòide-dodecaèdro s. m. – Poliedro convesso a 12 facce quadrangolari; è una delle forme semplici che possono assumere i cristalli di sostanze che cristallizzano in alcune classi del sistema monometrico.