derivata

derivata

derivata concetto fondamentale dellʼanalisi infinitesimale, che trova numerosissime applicazioni anche in tutte le scienze sperimentali. La derivata è una funzione dedotta (o derivata) in modo ben definito, da unʼaltra funzione. Si dice derivata della funzione reale (di variabile reale) ƒ(x) nel punto x̄ del suo insieme di definizione il limite (se esiste finito) del rapporto incrementale di ƒ al tendere a 0 dellʼincremento h = Δx della variabile indipendente x:

In termini intuitivi la derivata esprime la rapidità con cui varia ƒ(x) al variare di x in vicinanza di x̄. Il significato geometrico della derivata è quello di coefficiente angolare della tangente alla curva di equazione y = f(x) nel punto di ascissa x̄. Tale tangente ha dunque equazione

Nei punti in cui una funzione ƒ ammette derivata – o, come si usa dire, è derivabile – la funzione è necessariamente continua. Una funzione definita in un insieme I ⊆ R e derivabile per ogni x ∈ I è necessariamente continua in I. Non vale invece il viceversa perché una funzione può essere continua nel suo insieme di definizione, ma non derivabile in ogni suo punto; per esempio, la funzione valore assoluto y = |x| non è derivabile in x̄ = 0 pur essendo ivi continua. Infatti, si ha

e, poiché tale limite vale −1 o 1 a seconda che si consideri un incremento h negativo o positivo, non esiste il limite del rapporto incrementale della funzione per h tendente a 0. Il punto (0, 0) appartenente al grafico della funzione viene considerato come punto di non derivabilità, cioè punto in cui la funzione non è derivabile (e non esiste la tangente al suo grafico). Ovviamente i punti in corrispondenza dei quali la funzione non è continua sono anchʼessi punti di non derivabilità. Si può parlare, per estensione, in casi come quello dellʼesempio di derivata destra, così indicando il limite (finito) del rapporto incrementale per h → 0⁺, e di derivata sinistra, indicando invece il limite per h → 0⁻; tali derivate si designano rispettivamente coi simboli ƒʹ(x̄+) e ʹ(x̄–). Un punto in cui esistano derivata sinistra e derivata destra distinte è detto punto angoloso.

In alcuni contesti si accetta la locuzione derivata infinita nel caso in cui il limite del rapporto incrementale sia infinito e quindi la tangente sia parallela allʼasse delle ordinate.

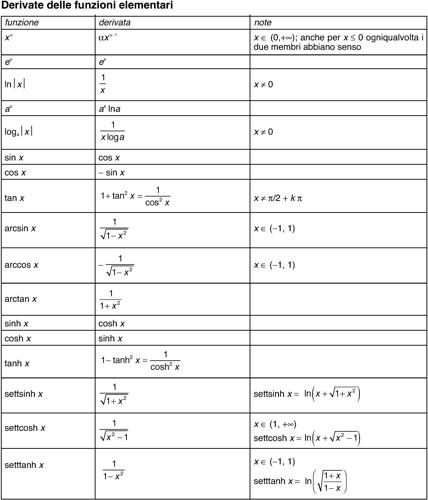
Il calcolo della derivata si riduce, nei casi più comuni, allʼapplicazione di alcune regole di → derivazione (riassumibili nella tavola delle regole di derivazione), utilizzando le derivate delle funzioni elementari (si veda la tavola delle derivate delle funzioni elementari).

Se una funzione ƒ è derivabile in tutti i punti di un insieme T, la funzione ƒ′(x) che esprime le sue derivate punto per punto è anchʼessa una funzione di x ed è detta funzione derivata di ƒ(x). La funzione derivata, definita in T, può ammettere a sua volta una derivata, che viene detta derivata seconda di ƒ(x) e designata con ƒ″(x). Se si può iterare il procedimento, si ottengono le derivate successive o derivate ennesime indicate con ƒ ⁽ⁿ⁾(x). Si stabilisce così un ordine delle derivate e si parla di derivata prima, derivata seconda, ..., derivata di ordine n, e conseguentemente di derivata dʼordine superiore o inferiore di unʼaltra. Per indicare la derivata di una funzione, oltre alla notazione ƒ′(x) (che si legge «effe primo di x») si utilizzano anche i simboli Dƒ(x) e

(questʼultima è detta notazione di → Leibniz). In fisica si usa a volte la notazione ẏ, molto frequente nei testi matematici del passato, per indicare la derivata di y = ƒ(x) (notazione di → Newton). Per le derivate successive, analogamente, si può scrivere

(→ differenziale).

Il concetto di derivata si estende a funzioni di più variabili y = ƒ(x₁, x₂, ..., x_n); si introduce così il concetto di → derivata parziale rispetto alla variabile x_i, ovvero la derivata della funzione della sola variabile x_i, ottenuta fissando i valori di tutte le altre variabili (→ gradiente). Per distinguerla dalle derivate parziali, talvolta per indicare la derivata di una funzione in una incognita si aggiunge al sostantivo derivata lʼaggettivo ordinaria.

Lʼestensione a funzioni a variabili complesse è possibile e porta a introdurre il concetto di → derivata complessa e quello di → funzione analitica. La nozione di derivata si estende poi, più in generale, al caso di applicazioni tra due spazi normati (derivata debole o di → Gâteaux e derivata forte o di → Fréchet).

: fig_lettD_01040_001.jpg>