destagionalizzazione
destagionalizzazione
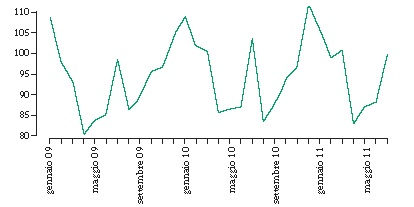
Metodo statistico atto a identificare e rimuovere le fluttuazioni di carattere stagionale di una serie storica, che impediscono di cogliere correttamente l’evoluzione dei fenomeni considerati. Esempi di serie che presentano stagionalità sono il tasso di disoccupazione, fortemente influenzato dalla natura stagionale di alcuni lavori, o l’indice della produzione industriale, la cui serie ‘grezza’ (non destagionalizzata) presenta una brusca caduta nei mesi estivi a causa della chiusura di molte fabbriche o imprese. Il grafico che segue mostra la serie degli indici della produzione industriale relativa al settore ‘D: fornitura di energia elettrica, gas, vapore e aria condizionata’, per il periodo gennaio 2009/luglio 2011 unità di misura in KW. Tale grafico evidenzia un aumento della produzione di energia nei mesi invernali, dovuto alla minor quantità di luce solare, e un incremento del fabbisogno di gas per il riscaldamento, ma anche un breve picco, in particolare nel mese di luglio, a causa dell’incremento di domanda di energia elettrica per il funzionamento dei condizionatori.
Nella decomposizione di una serie storica, si usa in genere considerare 4 componenti distinte: una, chiamata trend (Tt), che evidenzia la tendenza di lungo periodo della serie; una componente ciclica (Ct), che descrive fluttuazioni non periodiche generalmente legate al ciclo economico; una componente stagionale (St), che invece descrive fluttuazioni che si ripetono con una costante regolarità nel tempo, e infine un’ultima, idiosincratica (et), che descrive un termine di errore e rappresenta il residuo della serie. Il legame tra le componenti può essere di tipo additivo, Yt=a+Tt+Ct+St+et, o di altro genere, per es. moltiplicativo, come Yt=aTtCtStet. In quest’ultimo caso si ottiene un legame additivo dopo aver applicato all’equazione una trasformazione logaritmica (➔ logaritmica).
Molte procedure di d. si fondano su un trattamento preliminare dei dati, con il quale si effettua per es. la correzione dell’influenza di un diverso numero di giorni lavorativi nei periodi considerati, oppure della presenza di particolari festività o di altri eventi anomali che possano aver contribuito alla stagionalità. Dopo questo trattamento, si procede alla stima delle diverse componenti del modello. A tal fine si usano principalmente due approcci: uno è basato sull’applicazione di filtri lineari costituiti da medie mobili di diversa lunghezza, mentre l’altro parte dall’ipotesi di un particolare modello parametrico per la serie storica. Una volta eliminata dalla serie la componente corrispondente alla stagionalità (per es. considerando Yt−St nel caso di un modello additivo), si ottiene la serie destagionalizzata. La rimozione della stagionalità rende più semplici l’interpretazione e l’isolamento delle altre componenti.