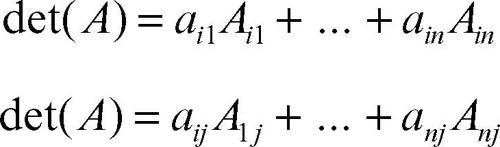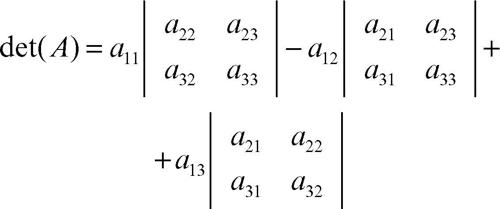determinante

determinante

determinante in algebra lineare, numero associato a una matrice quadrata A = [a_ij] di ordine n, indicato con det(A) o anche con |A|, uguale alla somma degli n! prodotti del tipo a_1σ(1) · a_2σ(2) · ... · a_nσ(n), ottenuti al variare di σ = {σ(1), σ(2), ..., σ(n)} tra le permutazioni dell’insieme {1, 2, ..., n}, ognuno preso con segno positivo se la permutazione σ è di classe pari, con segno negativo se la permutazione è di classe dispari. Formalmente, se S_n indica l’insieme delle permutazioni dell’insieme {1, 2, ..., n} e se sgn(σ) è la funzione che vale 1 se σ è di classe pari e −1 se σ è di classe dispari, allora det(A) è definito dalla formula

In particolare, per n = 1 si ha det(a₁₁) = a₁₁, per n = 2 si ha

_lettD_01410_002.jpg>

Una matrice A con determinante nullo è detta matrice singolare, se invece det(A) ≠ 0 allora A è detta non singolare. Il determinante esprime alcune proprietà molto importanti di una matrice, prima fra tutte la seguente: una matrice quadrata è invertibile se e solo se il suo determinante è diverso da zero, cioè se e solo se è non singolare. Se k ≤ n, un minore di ordine k di A è il determinante di una sottomatrice quadrata di A di ordine k, ottenuta cioè eliminando (n − k) righe e (n − k) colonne di A. Il complemento algebrico dell’elemento a_ij di A (indicato con il simbolo A_ij) è il minore di ordine (n − 1) ottenuto da A eliminando la i-esima riga e la j-esima colonna (cioè quelle in cui è contenuto l’elemento a_ij) preso con segno positivo se i + j è pari, negativo se invece i + j è dispari.

Per il calcolo del determinante di una matrice, si ricorre solitamente ad alcune regole e proprietà che possono ridurre notevolmente il numero dei calcoli altrimenti necessari. Una di queste è la regola per lo sviluppo del determinante di Laplace: il determinante di una matrice è uguale alla somma degli elementi di una sua fissata riga (o colonna) moltiplicati per i rispettivi complementi algebrici (ne segue che se una matrice a valori reali ha una riga (o una colonna) formata da elementi tutti nulli, il suo determinante è nullo). Formalmente, vale dunque

dove i e j sono gli indici rappresentanti una riga e una colonna arbitrarie: queste due espressioni sono dette rispettivamente lo sviluppo del determinante secondo la i-esima riga di A e secondo la j-esima colonna di A. Per esempio, data la matrice quadrata A di ordine 3

lo sviluppo del suo determinante secondo la prima riga è dato da:

Per semplificare il calcolo di una matrice del terzo ordine si ricorre in particolare alla regola di → Sarrus.

I determinanti hanno importanza fondamentale nella risoluzione dei sistemi di equazioni di primo grado (con la regola di Cramer) e proprio da tale problema traggono origine. Inoltre il calcolo del determinante fornisce la possibilità di stabilire, ancora prima di affrontare l’equazione, se il sistema ha o non ha soluzioni o se è indeterminato.

■ Proprietà del determinante.

a) Se v è un vettore riga (rispettivamente colonna) di una matrice A tale che v = aw₁ + bw₂ per qualche coppia di vettori w₁ e w₂ e se B₁ e B₂ sono le matrici ottenute da A sostituendo la riga (rispettivamente colonna) v con i vettori w₁ e w₂ rispettivamente, allora det(A) = adet(B₁) + bdet(B₂) (multilinearità);

b) se A′ è la matrice ottenuta da A scambiando due righe (rispettivamente due colonne), allora det(A′ ) = − det(A) (alternanza);

c) se A è triangolare, allora det(A) = a11 · a22 ·...· a_nn;

d) det (AB) = det(A) · det(B) (→ Binet, teorema di);

e) se AT è la matrice trasposta di A, allora det(A) = det(AT);

f) se A è invertibile, allora det(A⁻¹) = det(A)⁻¹.