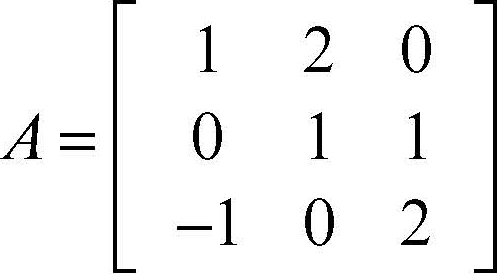diagonalizzazione
diagonalizzazione
diagonalizzazione in algebra lineare, procedura attraverso la quale, data una trasformazione lineare T di uno spazio vettoriale V su un campo K, se ne trova una equivalente espressa attraverso le sue direzioni di stiramento. Se V ha dimensione finita n e A è la matrice della trasformazione, ciò equivale a richiedere che la matrice A sia diagonalizzabile, cioè che esista una matrice quadrata invertibile P, di ordine n, tale che la matrice D = P−1AP sia una matrice diagonale, cioè con elementi non nulli solo sulla sua diagonale principale. La matrice D è detta forma diagonale di A, P è detta invece matrice diagonalizzante. La trasformazione (e, di conseguenza, la matrice) risulta diagonalizzabile se e solo se esiste una base di V costituita da autovettori per T. La diagonalizzabilità di una matrice A di dimensioni n × n, e quindi della trasformazione lineare T a essa associata, equivale all’esistenza di n assi coordinati passanti per l’origine che risultano rette unite in T e tali che su ciascuna di esse tutti i vettori non nulli sono autovettori con lo stesso autovalore. Su ciascuno di tali assi pertanto T risulta uno stiramento il cui rapporto è l’autovalore comune a tutti gli autovettori.
Definita la molteplicità geometrica di un autovalore k come la dimensione del relativo autospazio E(k), vale il seguente criterio: una matrice quadrata A, di ordine n, con elementi su un campo K, è diagonalizzabile se e solo se sono verificate entrambe le seguenti condizioni: 1) la somma delle molteplicità algebriche di tutti gli autovalori è n; 2) la molteplicità algebrica (ovvero come radice del polinomio caratteristico) e la molteplicità geometrica di ogni autovalore coincidono. Indicate rispettivamente con ma(k) e con mg(k) la molteplicità algebrica e la molteplicità geometrica di un medesimo autovalore k, in generale, si ha: 0 < mg(k) ≤ ma(k). Ne segue che se il polinomio caratteristico di A ha n radici distinte in K, la matrice, per il criterio precedente, è diagonalizzabile. Può accadere che una stessa matrice sia diagonalizzabile o meno a seconda del campo in cui variano i suoi elementi. Per esempio la matrice
non è diagonalizzabile in R, ma lo è in C. Infatti il suo polinomio caratteristico pA(λ) = −λ(λ2 − 4λ + 5) ha in R il solo autovalore 0 e per esso risulta mg(0) = ma(0) = 1, mentre in C ha tre autovalori distinti. Risultano diagonalizzabili tutte le matrici quadrate simmetriche a elementi reali e, più in generale, le matrici hermitiane. La matrice diagonalizzante P di una matrice simmetrica A è ortogonale, il che rende più semplice determinare la sua inversa, che risulta uguale alla sua trasposta.