differenze finite
differenze finite
Analogo discreto del differenziale (➔) nel continuo. Supponiamo di conoscere i valori di una funzione f(x) solo in certi punti equispaziati della variabile indipendente con spazio h fra due valori consecutivi. Definiamo differenza prima in avanti la Δ+f(x)=f(x+h)−f(x), differenza prima all’indietro la Δ−f(x)=f(x)−f(x−h); differenza prima centrale δf(x)=f(x+(1/2)h)−f(x−(1/2)h). Dividendo queste differenze per h si ottengono approssimazioni in avanti, all’indietro e centrali della derivata prima della f nel punto x. La differenza fra le approssimazioni e la derivata è infinitesima dello stesso ordine di h per le differenze in avanti e all’indietro, e di ordine h2 per la differenza centrale. Differenze del secondo ordine si ottengono facendo la differenza fra differenze del primo ordine: Δ2=f(x+h)−f(x)−(f(x)−f(x−h))=f(x+h)+f(x−h)−2f(x). Dividendo per h2 si ottiene un’approssimazione della derivata seconda.
Differenze finite nelle applicazioni all’economia e alla finanza
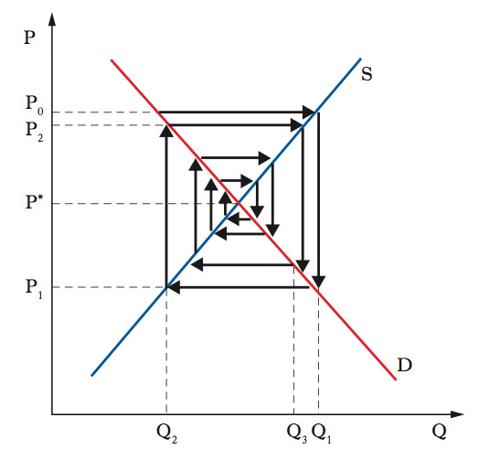
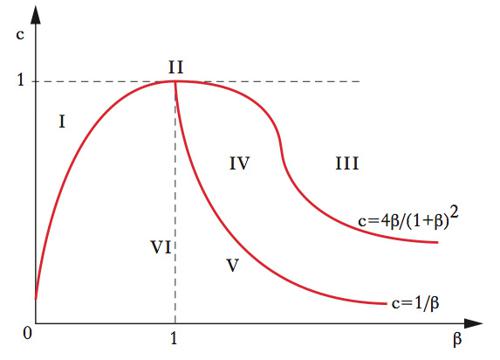
I metodi delle d. f. sono quelli che consentono di valutare i derivati risolvendo in via approssimata l’equazione differenziale che ne descrive il comportamento. A tal fine l’equazione differenziale viene convertita nella corrispondente equazione alle d. f., cioè un’equazione che mette in relazione una successione incognita yt con le sue differenze, ed essa (normalmente priva di soluzioni in forma chiusa) è risolta iterativamente. Il metodo ha dato buoni risultati nel prezzamento di opzioni put americane. Equazioni alle d. f. sono molto utilizzate in economia poiché la descrizione della dinamica del sistema economico si basa su dati riferiti a successioni di istanti di tempo equintervallati (mensili, trimestrali, semestrali o annuali). Il più semplice esempio di equazione alle d. f. è yt=kyt−1, dove k>0 (e diverso da 1, altrimenti banalmente yt=yt−1) è un parametro costante rispetto al tempo. Ponendo Δyt=yt−yt−1, l’equazione equivale alla Δyt=(k−1)yt−1. Essa è un’equazione del primo ordine (vi compaiono solo le differenze prime), lineare (la relazione fra l’incognita e la differenza è lineare), a coefficienti costanti e omogenea (non compaiono altre funzioni note del tempo). Nella versione non omogenea, ottenuta cioè con l’aggiunta al secondo membro dell’equazione omogenea di una successione nota xt (nel caso più semplice una costante c) che coglie l’influenza di variabili esogene, si ha Δyt=(k−1)yt−1+xt. Risolvere l’equazione significa trovare la successione, yt∗, che la soddisfa, a partire dalla condizione iniziale, cioè dal valore iniziale y0 supposto noto o scelto esogenamente. Nel caso xt=c, risulta yt∗=kt(y0−(c/(1−k)))+c/(1−k). Essa è interpretata come un sentiero o cammino in tempo discreto della variabile y. Trovata la soluzione, la questione sembrerebbe chiusa. Al contrario, e in particolare nelle applicazioni economiche, questa è solo la base di partenza per riflettere sulle proprietà della soluzione e chiarirne il reale significato. Per approfondire il problema prenderemo spunto dall’esempio forse più noto in letteratura: il cosiddetto modello della ragnatela (grafico 1). In esso compaiono equazioni lineari della domanda dt e dell’offerta st di un bene, in funzione del suo prezzo corrente pt e rispettivamente del prezzo pt−1 del periodo precedente, secondo le dt=α+βpt(β<0), st=γ+θpt−1(θ>0) e la condizione di eguaglianza (equilibrio istantaneo) fra domanda e offerta al tempo t, dt= st. Il modello traduce l’idea che, mentre la domanda si adegua immediatamente al prezzo corrente, la reazione dell’offerta è ritardata del tempo necessario a programmare la produzione. L’equazione alle differenze corrispondente è la pt=(θ/β)pt−1+(γ−α)/β, caso particolare della yt=kyt−1+c, con (θ/β) nel ruolo di k e (γ−α)/β in quello di c. Ne consegue immediatamente la soluzione pt∗=(γ−α)/(β−θ)+(p0−(γ−α)/(β−θ))(θ/β)t. Se p0=(γ−α)/(β−θ), si ha pt∗=p0 per ogni t, cioè un sentiero di prezzi di equilibrio a un livello costante (stazionario); altrimenti, con p0 diverso da (γ−α)/(β−θ), la sequenza dei prezzi di equilibrio istantaneo alterna prezzi maggiori e prezzi minori del livello di equilibrio stazionario (γ−α)/(β−θ). Solo nel primo caso la sequenza dei prezzi è di vero equilibrio; essa consente non solo di eguagliare a ogni istante domanda e offerta, ma di eguagliarle al livello coerente con il prezzo previsto al momento della programmazione dell’offerta. Per tale motivo il sentiero di equilibrio stazionario è definito equilibrio dinamico. Inoltre, se in valore assoluto (θ/β)<1, (θ/β)t e con essa (p0−(γ−α)/(β−θ))(θ/β)t tende a zero al crescere (più esattamente al divergere) di t, e quindi pt∗ tende all’equilibrio dinamico. In tal caso si dice che l’equilibrio dinamico è stabile, cioè se viene perturbato da qualche fattore esogeno al modello tende a essere automaticamente ripristinato. Al contrario, se in valore assoluto (θ/β)>1, (θ/β)t e con essa (p0−(γ−α)/(β−θ))(θ/β)t tende a infinito al crescere (più esattamente al divergere) di t, e quindi pt∗ si allontana sempre più dall’equilibrio dinamico (perciò definito instabile). Riassumendo, la stabilità implica che una eventuale deviazione casuale dall’equilibrio dinamico tende a essere progressivamente riassorbita; al contrario, in condizioni di instabilità, una, anche minima, perturbazione determina scostamenti sempre più ampi dall’equilibrio. Un altro modello di grandissimo rilievo nella storia del pensiero economico moderno, il cosiddetto acceleratore-moltiplicatore, dovuto a Samuelson, utilizza un’equazione alle d. f. del secondo ordine non omogenea. Il modello prevede un’equazione del consumo Ct=cYt−1, con 0<c<1 parametro di propensione al consumo del reddito Yt−1 del periodo precedente, un’equazione dell’investimento It=β(Ct−Ct−1) con β acceleratore dell’investimento endogeno in funzione della crescita del consumo nel periodo precedente, e la terza equazione che definisce il reddito nazionale come somma della spesa governativa autonoma, del consumo e dell’investimento Yt=G+Ct+It. Ne consegue l’equazione alle d. f. omogenea del secondo ordine Yt−c(1+β)Yt−1+ cβYt−2=G. L’equilibrio dinamico stazionario è in questo caso Y∗=G/(1−c), ottenuto moltiplicando la spesa autonoma per il fattore 1/(1−c) detto appunto moltiplicatore della spesa. La soluzione generale è Yt∗=A1λ1t+A2λ2t+G/(1−c), dove A1 e A2 sono fissate costanti, dipendenti dalle condizioni iniziali, e λ1, λ2 le soluzioni (radici) dell’equazione caratteristica λ2−c(1+β)λ+cβ=0, dove entrano in gioco i coefficienti della variante omogenea dell’equazione alle d. f. del secondo ordine che sintetizza il modello. Il comportamento del sistema dipende dal tipo di radici (reali o complesse; grafico 2). A radici reali (4β/(1+β)2<c<1) corrisponde convergenza (divergenza) monotona verso (in allontanamento da) l’equilibrio stazionario a seconda che cβ sia minore (zona I) o maggiore di 1 (zona III). A radici complesse (0<4β/(1+β)2) corrispondono fluttuazioni smorzate (cβ<1, zona VI), cicliche (cβ=1, curva V) o esplosive intorno all’equilibrio (cβ<1, zona IV), sempre in dipendenza dal valore del prodotto cβ. Nel punto (1,1) si ha una situazione stazionaria fuori dall’equilibrio dinamico.