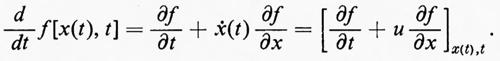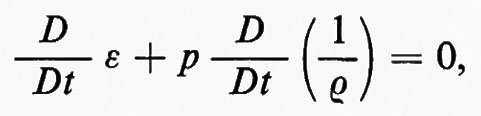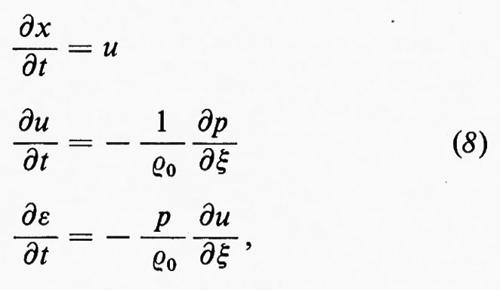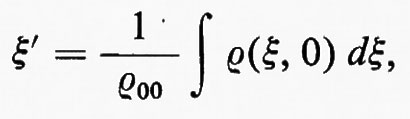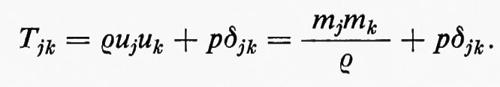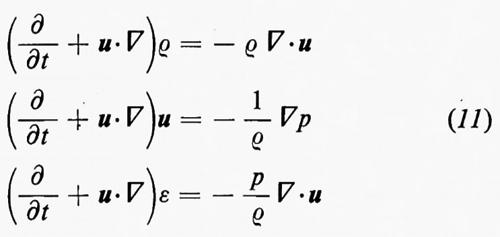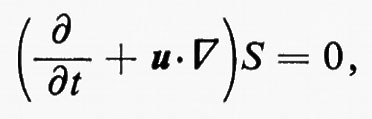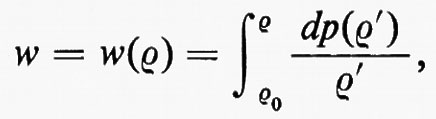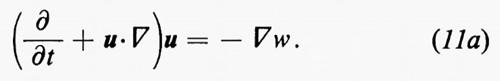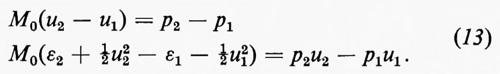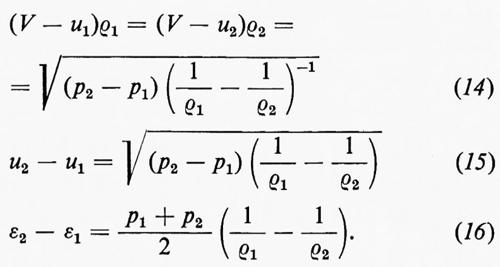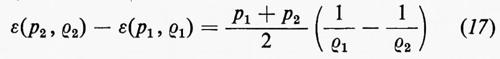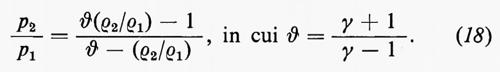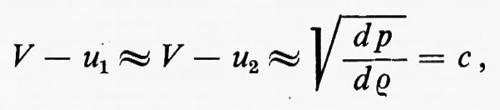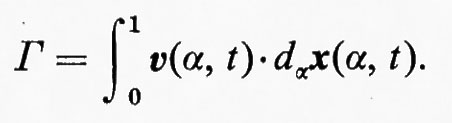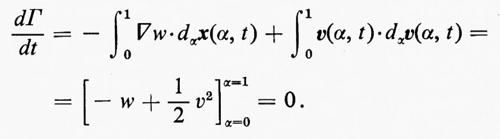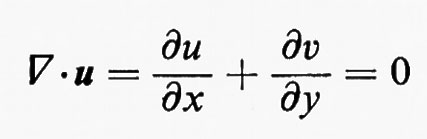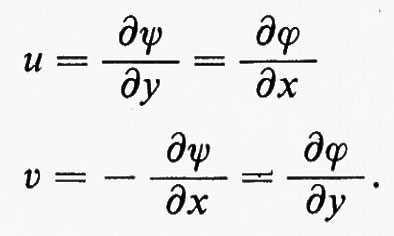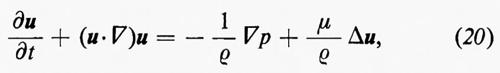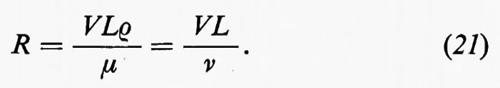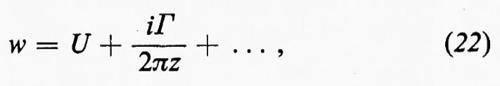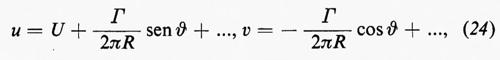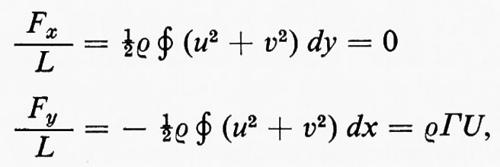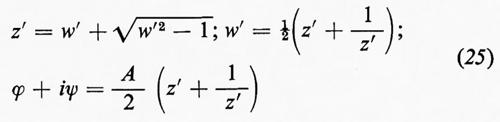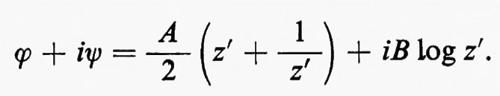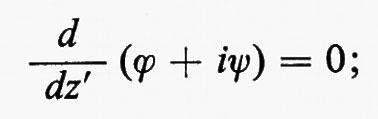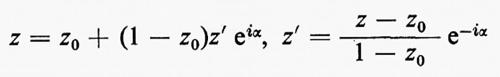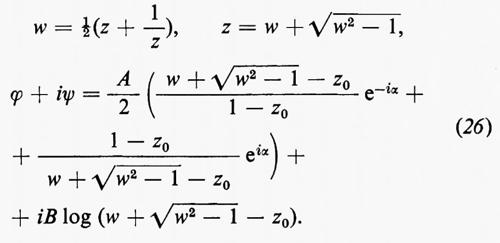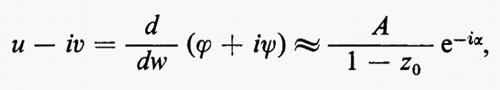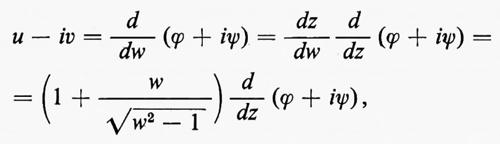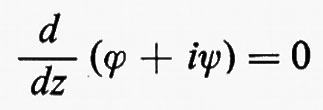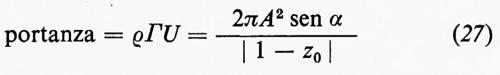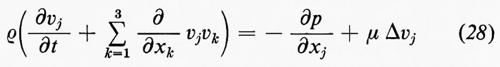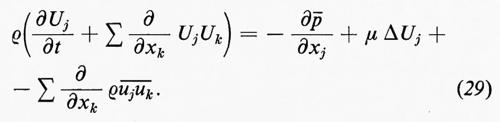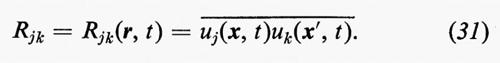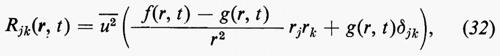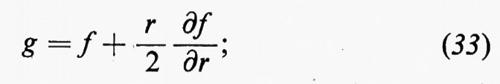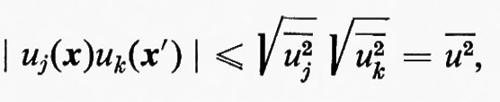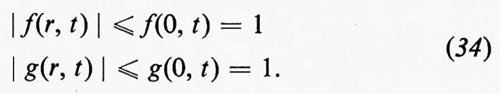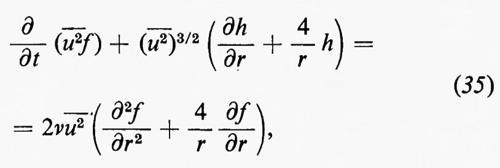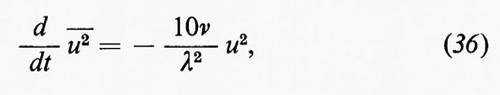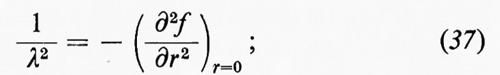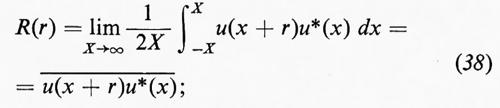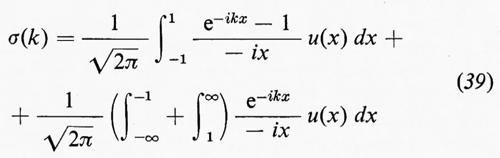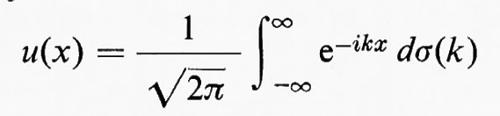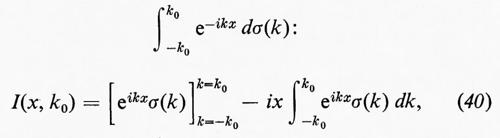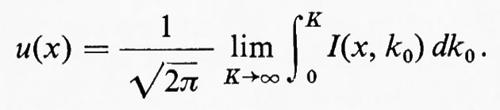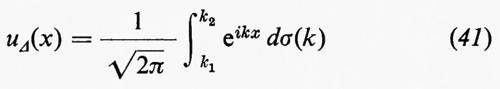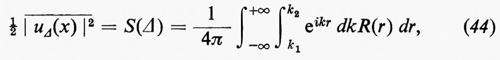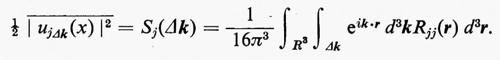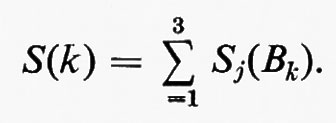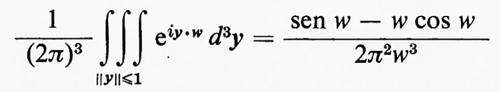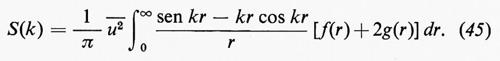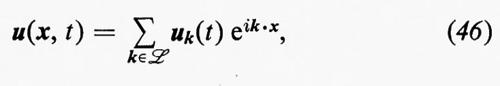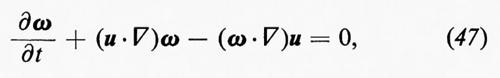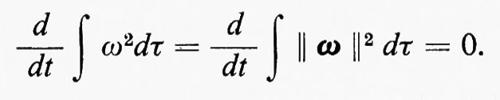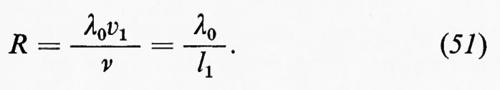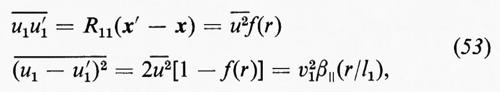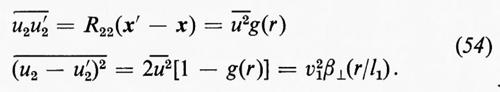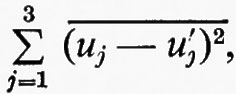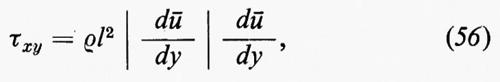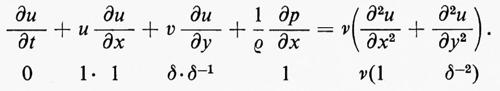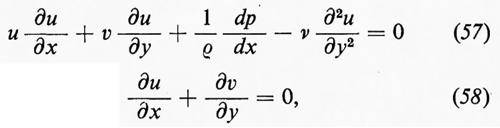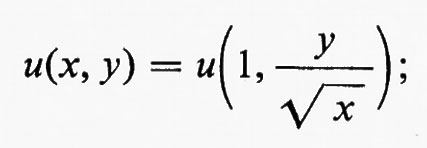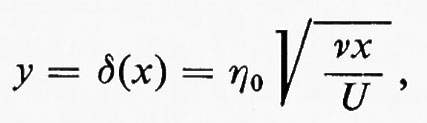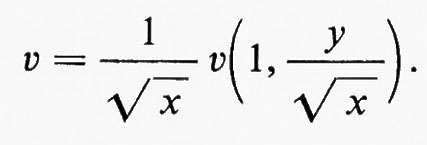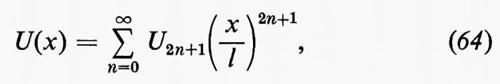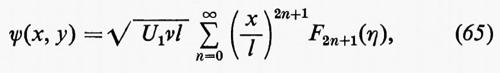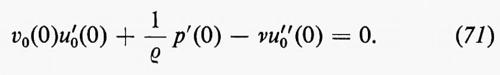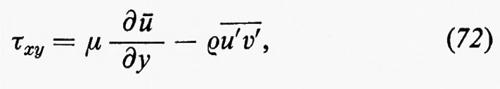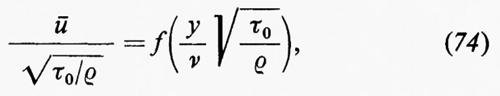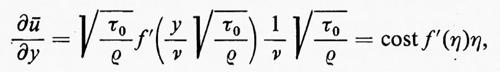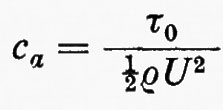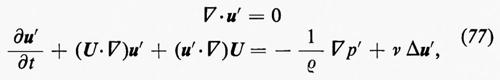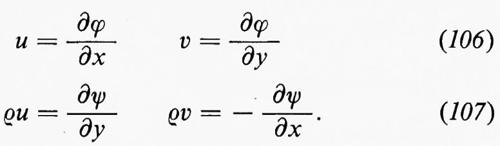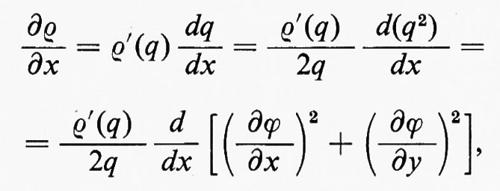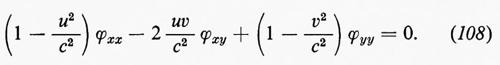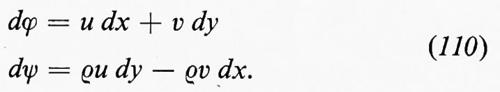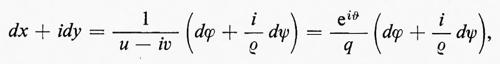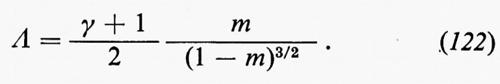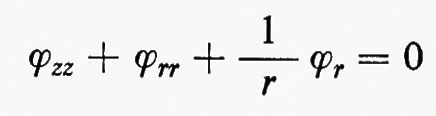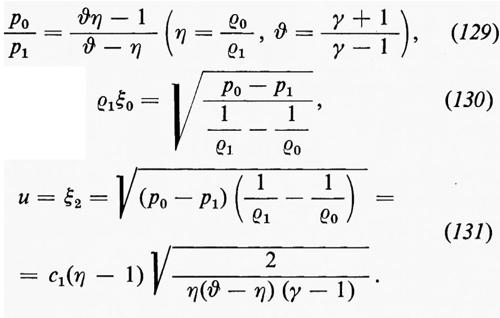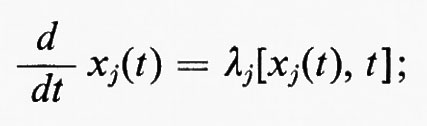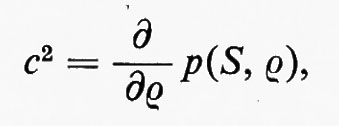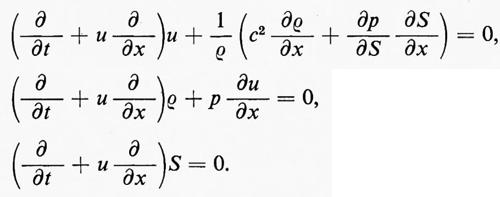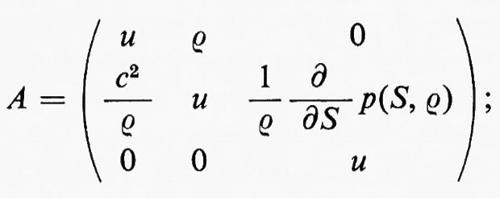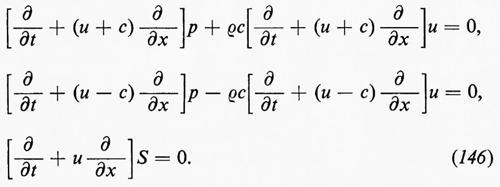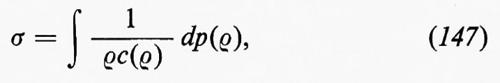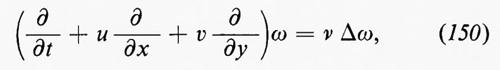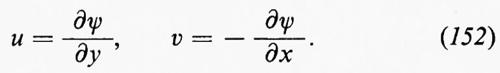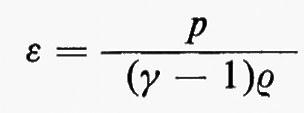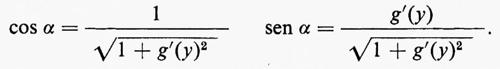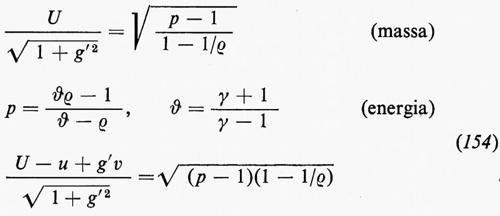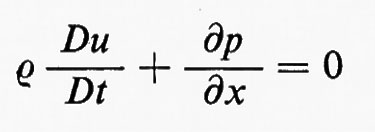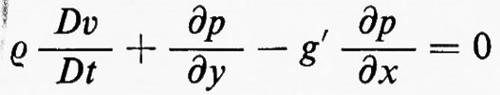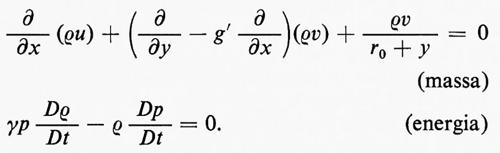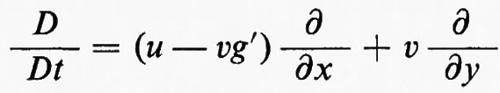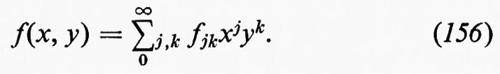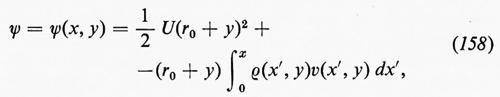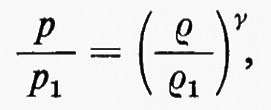Fluidi, dinamica dei

Fluidi, dinamica dei

di Robert D. Richtmyer

SOMMARIO: 1. Conoscenze all'inizio del secolo. □ 2. Le equazioni fondamentali: a) equazioni euleriane e lagrangiane; b) la legge dell'entropia; c) le equazioni di Lagrange; d) il caso tridimensionale; e) urti e superfici di slittamento; f) inesistenza di urti negativi; g) teorema di Kelvin per il flusso isoentropico; flusso potenziale; h) applicazioni dell'analisi complessa; i) flusso viscoso incompressibile; principio di similitudine di Reynolds. □ 3. Teoria dell'ala portante: a) il teorema di Žukovskij; b) esempio: il flusso attorno a un'ala di Žukovskij; c) ulteriori considerazioni. □ 4. Teorie statistiche della turbolenza: a) il tensore degli sforzi di Reynolds; b) correlazioni; c) lo spettro dell'energia; d) la cascata d'energia; l'intervallo inerziale e l'intervallo viscoso; e) distanza di mescolamento. □ 5. Strati limite: a) strato limite sopra una lamina piana; b) strato limite su una superficie curva; c) strato limite laminare nel flusso attorno a un cilindro circolare, trascurando l'effetto di distacco sul flusso esterno; d) distacco dello strato limite; e) teoria matematica delle equazioni dello strato limite; f) lo strato limite turbolento. □ 6. Instabilità dei flussi stazionari; insorgere della turbolenza: a) i principali problemi standard; b) flusso di Poiseuille in una condotta a sezione circolare; c) flusso di Poiseuille piano; d) flusso piano di Couette; e) flusso di Couette tra cilindri rotanti; f) strato limite su una lamina piana; teoria generale della stabilità dei flussi piani e paralleli, viscosi e non viscosi. □ 7. Convezione termica: a) il problema di Bénard; b) zone di convezione nelle stelle. □ 8. Alcuni aspetti analitici del flusso compressibile e non viscoso stazionario: a) rappresentazioni quasi conformi; b) le equazioni del flusso; c) la trasformazione odografa; d) il metodo di Bergman. □ 9. Problemi a valori iniziali per il flusso compressibile: a) il problema di Riemann; b) curve caratteristiche, il teorema di Cauchy-Kovalevskaja; c) generazione spontanea di urti; d) osservazioni sui casi multidimensionali; dipendenza continua dai dati iniziali. □ 10. Metodi di calcolo: a) metodi a differenze finite per un flusso non viscoso e compressibile dipendente dal tempo; b) raccordo delle discontinuità agli urti; pseudoviscosità; c) metodi a differenze finite per l'equazione di Navier-Stokes; d) metodi con serie di potenze; il problema dell'urto staccato; e) serie di potenze; prolungamento analitico; f) aritmetica significativa. □ 11. Osservazioni conclusive; problemi per il futuro. □ Bibliografia.

1. Conoscenze all'inizio del secolo.

In questo articolo per fluidi si intendono i gas normali e i liquidi e non, per esempio, i plasmi, i gas rarefatti o i solidi sottoposti a deformazioni plastiche. I fluidi possono essere compressibili, viscosi, soggetti alla tensione superficiale e a forze di volume (essenzialmente la gravità). Non saranno prese in considerazione le reazioni chimiche, la conducibilità termica e gli effetti elettromagnetici.

I fondamenti della dinamica dei fluidi del XX secolo erano già ben stabiliti sin dal 1900. Studi teorici e sperimentali sui fluidi incompressibili (v. Lamb, 1932⁴) erano stati compiuti nei casi di flussi entro condotte e canali, nel caso delle onde nell'acqua, della resistenza superficiale e ondosa al moto di una nave, dell'azione delle eliche delle navi, compresi gli effetti di cavitazione, e nel caso del flusso in turbine, valvole e chiuse per istallazioni idroelettriche. Gli strumenti teorici (v. sotto) includevano la legge di Bernoulli, l'equazione di Laplace per il flusso derivante da potenziale, le equazioni dinamiche di Eulero e Lagrange per i fluidi non viscosi, i teoremi di Helmholtz e di Kelvin sui vortici, il lavoro di Reynolds sulla stabilità del flusso laminare e quello di Helmholtz sulla stabilità di una superficie di scorrimento. I risultati comprendevano la legge di Hagen-Poiseuille sul flusso laminare in un tubo, la legge di Newton per la resistenza da turbolenze, le formule per la velocità di propagazione delle onde di gravità in acque basse o profonde, nozioni di progettazione efficiente di scafi ed eliche per navi, ecc.

Si era giunti a una buona comprensione dei fenomeni acustici nei fluidi compressibili (v. Rayleigh, 1945²). Era noto che un generico fluido compressibile e non viscoso è governato, in assenza di urti o di altre singolarità, dalle equazioni di Eulero e Lagrange prima citate, convenientemente modificate per tener conto della compressibilità. Un risultato consisteva nel paradosso di D'Alembert, per il quale le equazioni sembravano indicare che su un corpo in moto in un fluido non viscoso non si esercitasse alcuna forza. Il paradosso fu risolto più tardi, in seguito ai lavori di Helmholtz, Kirkhoff e Rayleigh, che presero in considerazione la circuitazione. L'effetto Magnus, consistente nella nascita di una forza laterale su di un oggetto rotante in movimento, come una palla da tennis ruotante su se stessa, era stato facilmente spiegato da Rayleigh usando la legge di Bernoulli.

Erano stati compresi i fondamenti fisici di flusso supersonico e delle onde d'urto. Riemann aveva risolto il problema ai valori iniziali di una discontinuità iniziale nella pressione o nella velocità di un fluido, o in entrambe, con condizioni costanti da ambedue le parti della discontinuità (v. sotto, cap. 9, È a). Nel trattare questo problema egli aveva commesso un errore, basando le condizioni di discontinuità dalle due parti di un'onda d'urto sulla conservazione della massa, della quantità di moto e dell'entropia, piuttosto che della massa, della quantità di moto e dell'energia. In seguito questo errore fu corretto da Rankine e Hugoniot; esso, comunque, non aveva influenzato il carattere della soluzione. La teoria delle caratteristiche e degli invarianti di Riemann (v. sotto, cap. 9, È b) aveva reso possibile la soluzione di vari problemi nel caso di flussi in fluidi compressibili. Mach aveva studiato il flusso supersonico attorno a un proiettile mediante il metodo strioscopico da lui sviluppato.

La teoria della turbolenza era ai suoi inizi con il lavoro di Reynolds in cui si enunciava il principio di similitudine associato al parametro adimensionale più tardi chiamato da Sommerfeld ‛numero di Reynolds'. Era stata derivata l'equazione fondamentale di Navier-Stokes per un fluido viscoso incompressibile (in seguito anche compressibile) che governa, tra le altre cose, la turbolenza. Reynolds aveva introdotto la formula per lo sforzo medio dovuto alla turbolenza, adesso noto come ‛sforzo di Reynolds' (v. sotto, cap. 4, È a).

Per quanto durante il XX secolo (o, per lo meno, fino a questi ultimi anni) non sia stato enunciato nessun principio sostanzialmente nuovo nella dinamica dei fluidi, come è stata qui definita, le applicazioni a campi come l'aeronautica e l'astrofisica sono state numerose e importanti. La teoria dello strato limite è uno dei maggiori risultati e i problemi di turbolenza e di convezione si sono rivelati tra i più ardui mai posti alla fisica matematica.

2. Le equazioni fondamentali.

Il moto di un fluido è governato dalle leggi fondamentali sulla massa, sulla quantità di moto e sull'energia, dalle relazioni termodinamiche tra pressione, densità ed energia interna (equazione di stato) e dalla legge della viscosità. (In varie applicazioni, a queste relazioni vanno aggiunte le leggi di altri fenomeni fisici, come la tensione superficiale, la conduzione del calore e la gravità). Descriveremo subito le leggi fondamentali, in forma appropriata per un fluido, con notazioni e terminologia moderne.

Per prima cosa, consideriamo flussi unidimensionali di fluidi non viscosi, corrispondenti, per esempio, in pratica, al caso di un fluido che si muova senza attrito in una condotta di sezione unitaria. Siano u, p, ρ, ε rispettivamente la velocità, la pressione, la densità e l'energia interna per unità di massa. Queste grandezze sono funzioni di una coordinata cartesiana x e del tempo t:u=u(x, t), ecc. Conviene introdurre, come ulteriori variabili dipendenti, la quantità di moto, o momento, per unità di volume, m=ρu, e l'energia totale per unità di volume, e=ρε+½ρu². Il moto di due particelle sia descritto dalle funzioni x=a(t) e x=b(t), con a(t)〈b(t). La parte di fluido che occupa la regione a(t)〈x〈b(t) avrà massa, momento ed energia totali dati da

In base alle leggi della meccanica sarà Í=0 (il punto indica la derivata rispetto al tempo), Ñ sarà uguale alla somma delle forze agenti su quella parte del fluido ed Ė al lavoro che queste forze compiono nell'unità di tempo. Quindi, sarà:

Í=0

Ñ=−p(b, t)+p(a, t) (2)

Ė=−p(b, t) u(b, t)+p(a, t) u(a, t).

Ognuna di queste equazioni, si noti, ha la forma

È un'osservazione generale il fatto che un flusso consista di flussi regolari in certe regioni, dove le funzioni e le loro derivate sono continue, separate da superfici che rappresentano urti, discontinuità di contatto e simili. Le leggi fondamentali sono espresse da equazioni a derivate parziali nelle regioni di flusso regolare e da condizioni di discontinuità attraverso le superfici di separazione.

a) Equazioni euleriane e lagrangiane.

Nelle regioni di flusso regolare, un'equazione del tipo (3) può essere riscritta come segue:

perché ȧ=u(a, t) e ???35???=u(b, t); quindi:

Questo vale per ogni intervallo (a, b); pertanto, dato che le derivate parziali sono funzioni continue, l'espressione contenuta tra parentesi quadre è identicamente nulla e ne risulta un'equazione a derivate parziali nella forma di una ‛legge di conservazione': ∂f/∂t+∂k/∂x=0. Se si applica questo procedimento alle equazioni (1) e (2), si ottiene:

Se si scrive l'equazione di stato nella forma p=f(ε, ρ) - per un gas perfetto è p=(γ−1)ρε, con γ costante -, allora si ha per p, in funzione delle variabili dipendenti ρ, m, e che appaiono a primo membro delle equazioni scritte sopra:

Il simbolo p nella (4) va pertanto inteso come un'abbreviazione di questa espressione.

Le equazioni possono anche essere scritte in vari modi come un sistema quasilineare, per esempio:

con p=f(ε, ρ). L'operatore indicato tra parentesi talvolta si scrive come D/Dt; esso consiste in una differenziazione eseguita rispetto al tempo in un sistema di riferimento che segue il moto della particella, perché, se x(t) è la coordinata della particella, allora è:

Le equazioni a derivate parziali (4) o (6), insieme a condizioni iniziali e spesso anche a condizioni al contorno, costituiscono il generico problema a valori iniziali della dinamica dei fluidi unidimensionali non viscosi.

b) La legge dell'entropia.

Siano T(x, t) e S(x, t) la temperatura assoluta e l'entropia per unità di massa. Secondo le leggi della termodinamica, S e T sono anche funzioni di ε e ρ, legate in modo che

La prima e la terza delle equazioni (6) possono essere combinate per dare

dove D/Dt=∂/∂t+u∂/∂x, come sopra. Questo corrisponde a porre DS/Dt=0, da cui si vede che l'entropia è costante lungo la traiettoria delle particelle, nella parte regolare del flusso. Quando l'entropia S è costante inizialmente, cioè indipendente da x, rimane sempre costante fintanto che il flusso rimane regolare, senza fronti d'urto. In questo caso il flusso si dice ‛isoentropico', la terza equazione del sistema (6) non è più necessaria e l'equazione di stato è sostituita da una relazione p=p(ρ), tra p e ρ a entropia costante, che, nel caso di un gas perfetto, è p=p₀(ρ/ρ₀)^γ.

L'analisi di Riemann del problema a valori iniziali, nel caso isoentropico, usando il metodo delle caratteristiche, è descritta brevemente nel cap. 9, È a.

Le equazioni (6) sono dette ‛equazioni euleriane' del moto. Più in generale, ogniqualvolta le variabili spaziali indipendenti sono coordinate (cartesiane o curvilinee generiche) di un sistema di riferimento fisso, rispetto al quale il fluido si sta muovendo, le equazioni del moto sono dette ‛euleriane'.

c) Le equazioni di Lagrange.

Nelle ‛equazioni lagrangiane' del moto le variabili indipendenti individuano singoli elementi del fluido e la posizione di un elemento rispetto al sistema fisso, all'istante t, è descritta da variabili dipendenti. Nel caso unidimensionale, siano x(ξ, t) la coordinata x all'istante t di un elemento di fluido che era in x=ξ all'istante t=0 e ρ(ξ, t), u(ξ, t) e p(ξ, t) le sue densità, velocità e pressione. L'operatore di differenziazione temporale nel sistema che segue l'elemento di fluido, prima scritto come ∂/∂t+u(∂/∂x) si riduce ora semplicemente a ∂/∂t; quindi due delle equazioni (6), insieme alla ovvia equazione che connette u e x, costituiscono il sistema

dove ρ₀=ρ₀(ξ) è la densità iniziale ρ(ξ, o); essa compare nelle (8) perché ρdx=ρ₀dξ. In realtà dx/dξ è il rapporto tra il volume dell'elemento di fluido e il suo volume iniziale, quindi ρ=ρ(ξ, t) non è dato da un'equazione contenente ∂/∂t, ma da

Queste equazioni, come quelle di Eulero, vanno completate con un'equazione di stato p=f(ε, ρ).

Chiaramente, la scelta della coordinata iniziale ξ per individuare l'elemento di fluido era arbitraria. ξ potrebbe essere sostituita da ogni altro parametro ξ′ che sia una funzione crescente, o decrescente, di ξ, con un opportuno cambiamento nella funzione ρ₀(ξ). In particolare, se

allora la funzione ρ₀(ξ) è sostituita, nelle (8) e (9), dalla costante ρ₀₀.

Per calcoli numerici in problemi a una sola variabile spaziale (per esempio, una coordinata cartesiana o la coordinata radiale in problemi a simmetria sferica) è conveniente l'uso delle equazioni di Lagrange, specialmente quando sono presenti vari fluidi di tipo diverso o quando, come nella diffusione turbolenta, si desidera seguire il moto dei singoli elementi di fluido. Vari motivi rendono le equazioni di Lagrange non adatte alla maggior parte dei problemi multidimensionali: la derivata parziale nella (9) va sostituita con lo jacobiano della trasformazione ξ, η, ζ→x, y, z effettuata dal flusso nell'intervallo di tempo compreso tra 0 e t; in più, un elemento inizialmente cubico, di volume dξdηdζ, viene distorto e assume una forma spesso molto allungata in un breve tempo; questo rende imprecise le soluzioni ottenute basandosi su metodi a differenze finite.

d) Il caso tridimensionale.

Adesso verranno date le equazioni di Eulero per il caso a tre dimensioni, in coordinate cartesiane, nella forma ‛legge di conservazione' e nella forma più usuale corrispondente alle (6). Il momento specifico m ha adesso tre componenti, m₁, m₂, m₃, e ci sono cinque equazioni corrispondenti alle (4). Queste sono

dove gli indici delle sommatorie vanno da 1 a 3 e T_jk denota il tensore degli sforzi:

Le equazioni corrispondenti alle (6) sono

nella usuale notazione vettoriale.

Come nel caso unidimensionale, da queste equazioni segue che

dove S=S(x, t) è l'entropia per unità di massa. Quindi S, se per t =0 non dipende da x, rimane costante per ogni t≥0, fintanto che non compaiono urti; il flusso si dice isoentropico. Se p=p(ρ), per un determinato valore dell'entropia, e se si pone

dove ρ₀ è un valore di riferimento fissato della densità, la seconda equazione delle (11) diventa

e) Urti e superfici di slittamento.

La discussione che abbiamo iniziato nel paragrafo a) è valida per la parte regolare del flusso, nella quale le quantità u(o u), p, ρ e ε, come funzioni di x(o x) e t, sono funzioni di classe C¹, pertanto hanno senso le derivate che appaiono nelle equazioni differenziali. Discuteremo adesso le condizioni di discontinuità attraverso una superficie in cui le grandezze di flusso o le loro derivate prime abbiano discontinuità semplici, per le quali cioè siano ben definiti i valori limite su ogni faccia della superficie. Per l'economia della presentazione, notiamo per prima cosa che quando le grandezze di flusso sono continue, e hanno discontinue solo le derivate, non è necessaria nessuna condizione di discontinuità, oltre alla continuità delle grandezze di flusso stesse. Questo vale, per esempio, all'inizio e al termine di un'onda di rarefazione (v. sotto, cap. 9, È a). Questo risultato, che non verrà dimostrato, segue dalle leggi di massa, momento ed energia, allo stesso modo di come ne derivano le condizioni di discontinuità, leggermente più complicate, per urti e superfici di slittamento, che adesso discuteremo.

Per prima cosa consideriamo un urto in un flusso unidimensionale. Per semplicità supponiamo che il fronte d'urto si muova con velocità costante V e che le grandezze di flusso abbiano valori costanti sia davanti (u₁, p₁, ρ₁, ε₁) sia dietro (u₂, p₂, ρ₂, ε₂) al fronte d'urto. Data la compressione del fluido da parte dell'urto, sarà p₂>p₁ e ρ₂>ρ₁. Si suppone anche che sia V>u₁ e V>u₂, cioè che l'urto si stia muovendo nella direzione +x rispetto al fluido (il caso inverso essendo del tutto analogo). La massa di fluido raggiunta dall'urto per unità di tempo e per unità d'area del fronte d'urto è (V−u₁) ρ₁, evidentemente uguale a (V−u₂)ρ₂, in virtù del principio di conservazione della massa. Quindi è:

M₀^def=(V−u₁)ρ₁=(V−u₂)ρ₂. (12)

La variazione del momento di questo fluido, nel passaggio attraverso il fronte d'urto, è uguale alla risultante delle forze di pressione che agiscono su di esso e la variazione di energia è uguale al lavoro fatto da queste forze; quindi

Queste equazioni possono essere riscritte in vari modi, uno dei quali è

In questa forma esse sono note come condizioni di discontinuità di Rankine-Hugoniot. Sebbene in questo caso siano state ricavate supponendo costanti le condizioni dalle due parti del fronte, esse sono valide in generale e servono a connettere le soluzioni delle equazioni differenziali dalle due parti e a determinare la velocità V=V(t) con cui il fronte stesso si muove.

Se si scrive l'equazione di stato nella forma ε=ε(p, ρ), la (16) diventa

e mostra che, dati p₁ e ρ₁ esiste una famiglia di possibili stati finali, p₂, ρ₂, dipendente da un unico parametro. Il grafico risultante di p₂ in funzione di ρ₂ è detto curva di Hugoniot; ogni punto della curva rappresenta uno stato finale che può essere ottenuto dallo stato iniziale per compressione dovuta a un unico urto. La fig. 1 mostra schematicamente la curva di Hugoniot nel caso di un gas perfetto, per il quale ε(p, ρ)=p/(γ−1)ρ; in questo caso l'equazione (17) porta a un legame tra il rapporto di pressione p₂/p₁ e il rapporto di densità ρ₂/ρ₁ dato da

Le principali caratteristiche della curva di Hugoniot sono: 1) al punto p₁, ρ₁ ha la pendenza e la curvatura della curva a entropia costante p=cost ρ^γ, quindi, per urti deboli, l'incremento di entropia causato dall'urto è del terzo ordine nell'intensità dell'urto; 2) al tendere del rapporto di densità al valore ϑ, p₂ tende all'infinito, per cui con un singolo urto non si può ottenere una compressione di un fattore più grande di ϑ (≈ 6 per l'aria).

Per un urto debole, in cui p₂ e ρ₂ sono solo poco più grandi di p₁ e ρ₁, dall'equazione (14) si ricava:

dove la derivata, calcolata a entropia costante, è pari al quadrato della velocità c del suono. Quindi un urto debole viaggia alla velocità del suono rispetto al fluido. Nel caso di urti più forti si può dimostrare che V−u₁ è superiore alla velocità del suono, c₁, nel fluido davanti all'urto, mentre V−u₂ è inferiore alla velocità del suono, c₂, nel fluido dietro l'urto. Quindi l'urto sorpassa le perturbazioni elastiche che lo precedono ed è sorpassato da quelle che lo seguono. Per cui, se ci sono due urti, uno di seguito all'altro, il secondo può raggiungere il primo e allora si fondono entrambi in un unico urto.

f) Inesistenza di urti negativi.

Si è supposto che sia p₂>p₁ e ρ₂>ρ₁. Tuttavia, se si scambiano p₂, ρ₂, u₂ ed ε₂ rispettivamente con p₁, ρ₁, u₁ ed ε₁, tutte le equazioni comprese tra la (12) e la (17) rimangono valide. La discontinuità continua a muoversi nella direzione +x rispetto al fluido, perché V−u₁ e V−u₂ sono positivi, ma in questo caso si ha un'improvvisa decompressione del fluido invece di una sua improvvisa compressione. La soluzione delle equazioni rappresenterebbe pertanto un urto negativo, che in natura non si registra mai. La possibile esistenza di soli urti positivi, e non negativi, può essere capita sulla base di tre considerazioni diverse. La prima riguarda la stabilità. Supponiamo che un urto positivo, d'intensità p₂−p₁, sia sostituito da un grande numero N di urti più piccoli, ognuno d'intensità (p₂−p₁)/N, e separati ognuno dal successivo da una distanza molto piccola. Se questa è sufficientemente piccola, la curva di p in funzione di x mostrerà una sola discontinuità, entro gli errori di osservazione. Inoltre, secondo quanto notato nel paragrafo precedente, questi piccoli urti si fonderanno in un unico urto in un tempo molto breve. Se si pensa di fare lo stesso con un urto negativo, i singoli urti non si fonderanno, ma al contrario si separeranno sempre di più col procedere del tempo e presto la curva di p in funzione di x rappresenterà un'onda di rarefazione. Come seconda considerazione, notiamo che l'entropia di un fluido è aumentata da un urto positivo, ma verrebbe diminuita da uno negativo: non essendovi un corrispondente aumento di entropia da altre parti, si violerebbe in tal modo la seconda legge della termodinamica. Terzo e ultimo punto: se nelle equazioni vengono inclusi fenomeni dissipativi, come la conducibilità termica e la viscosità, si trova che per un urto positivo esiste una soluzione che porta a uno stato stazionario, in cui la transizione dallo stato p₁, ρ₁ allo stato p₂, ρ₂ ha luogo con continuità in uno strato molto sottile, attraverso il quale le condizioni di discontinuità di Rankine-Hugoniot sono soddisfatte, mentre una soluzione di questo tipo non esiste per un urto negativo (v. Richtmyer e Morton, 1967).

g) Teorema di Kelvin per il flusso isoentropico; flusso potenziale.

Si consideri un flusso isoentropico in una regione R dello spazio e sia C₀ una curva chiusa in R, data da x=x₀(α), α essendo un parametro reale per il quale 0≤α≤1, e x₀(1)=x₀(0). Sia x(α, t) la posizione, all'istante t, della particella di fluido che si trovava in x₀(α) all'istante t =0. Per un t fissato, x(α, t) traccia una curva chiusa C=C(t) per α che varia da 0 a 1, con C(0)=C₀. La curva C(t) si muove col fluido. Chiaramente (∂/∂t)x(α, t) è la velocità del fluido alla posizione x(α, t) e all'istante t, che chiameremo v(α, t). Se il campo di velocità è detto u(x, t), come al solito, dall'equazione del moto (11a) segue che

L'integrale

Γ=Γ(t)=§_C u•dx

si chiama circuitazione di u lungo la curva C. In forma esplicita è:

Quindi

Questo è il risultato del teorema di Kelvin il cui enunciato asserisce che la circuitazione su una curva chiusa che si muova col fluido in un flusso isoentropico è costante nel tempo.

Se R è semplicemente connessa, la condizione che Γ si annulli per ogni curva chiusa in R è equivalente alla condizione che u sia, in R, il gradiente di uno scalare: u=∇ϕ, e anche alla condizione che la vorticità, ω=∇⋀u, sia nulla in R. Dal teorema di Kelvin segue che, se ω≡0 per t=0, allora ω≡0 per ogni t≥0, finché non intervengono urti. Questo è un ‛flusso potenziale' e u=∇ϕ.

h) Applicazioni dell'analisi complessa.

Per un flusso potenziale incompressibile le equazioni ∇•u=0 e u=∇ϕ implicano che il potenziale soddisfi l'equazione di Laplace ∆ϕ=0. Reciprocamente, ogni funzione ϕ(x, t)=ϕ(x, y, z, t) che soddisfi l'equazione di Laplace rispetto a x, y e z e che abbia derivata continua rispetto a t (in modo che ∂u/∂t sia definita) determina un flusso possibile. Poiché in un fluido incompressibile la velocità del suono è infinita, la dipendenza dal tempo è una proprietà globale dipendente esclusivamente dall'eventuale moto di pareti rigide e da altre condizioni ausiliari.

Nel caso bidimensionale l'equazione

permette d'introdurre una corrente ψ tale che

Queste sono le equazioni di Cauchy-Riemann; ne segue che Φ(z), definita come ϕ+iψ, è una funzione analitica di z=x+iy e che u−iv=Φ′(z) è pure una funzione analitica di z. Un esempio di soluzione di un problema di fluidodinamica mediante funzioni analitiche è dato nel paragrafo che segue.

i) Flusso viscoso incompressibile; principio di similitudine di Reynolds.

Le equazioni di Eulero (11) possono essere modificate includendovi termini che rappresentano gli effetti della viscosità. In questo caso il problema si semplifica notevolmente se il fluido è trattato come incompressibile: un fluido compressibile, infatti, ha due coefficienti di viscosità ed effetti di viscosità devono essere inclusi nell'equazione dell'energia (v. Landau e Lifshitz, 1959; v. Monin e Yaglom, 1971). Per un fluido incompressibile le equazioni sono:

∇•u=0 (19)

dove μ è il coefficiente di viscosità del fluido. Queste sono le equazioni di Navier-Stokes; μ/ρ è detta ‛viscosità cinematica' ed è usualmente indicata con ν. L'approssimazione di incompressibilità è valida per molti casi; alcuni fenomeni in cui compressibilità e viscosità interagiscono saranno citati brevemente, come esempio, alla fine del cap. 6. Poiché le equazioni (19) e (20) sono invarianti rispetto a certi cambiamenti di scala nelle variabili dipendenti e indipendenti e nelle costanti che appaiono in esse, Reynolds fu portato a formulare il seguente principio di similitudine: la formulazione di un problema di fluidodinamica normalmente contiene una velocità caratteristica V (la velocità di volo di un aeromobile o la velocità media di flusso in un condotto) e una lunghezza caratteristica L (la dimensione di un'ala o il diametro del condotto). Esiste una combinazione adimensionale delle costanti μ, ρ, V, L, detta, per l'appunto, ‛numero di Reynolds', data da:

Tutte e quattro le costanti variano da un problema all'altro, μ e ρ dipendendo dalla pressione, dalla temperatura e dalla natura del fluido. Ma se variano in modo tale da lasciare immutato R, resta immutata anche la soluzione, purché si prenda L come unità di misura per tutte le lunghezze, V per le velocità, L/V per i tempi, ρV² per le pressioni e così via. In particolare, se si effettuano cambiamenti di scala di questo tipo, alcune proprietà generali della soluzione (per esempio il fatto che un flusso sia stabile o instabile) dipendono solo dal valore di R.

3. Teoria dell'ala portante.

Il primo volo a motore fu realizzato quando ancora le conoscenze teoriche erano molto scarse. Prima che il volo aereo fosse reso sicuro ed efficiente, fu necessario capire il meccanismo della portanza e della resistenza aerodinamiche, il fenomeno dello stallo, l'effetto e il controllo della turbolenza, il funzionamento delle eliche e delle superfici di controllo. Si giunse alla comprensione di tutto questo nel periodo compreso tra il 1900 e il 1940 grazie, in parte, allo sviluppo delle gallerie aerodinamiche e degli apparecchi di misura e, in parte, ai progressi teorici. Il lavoro teorico portò alla conoscenza di molti principi fisici essenzialmente nuovi, anche se basati su leggi ed equazioni che erano ben conosciute già nel 1900.

La prima teoria della portanza alare fu sviluppata principalmente dallo studioso di aerodinamica russo Žukovskij, dal matematico tedesco Kutta e dall'ingegnere inglese Lanchester. In tale teoria si assume il caso che l'ala sia molto lunga e a sezione costante lungo l'intera lunghezza, in modo che il flusso possa essere considerato con buona approssimazione bidimensionale. Si suppone, in base al teorema di Kelvin, che il flusso sia irrotazionale, tranne che in uno strato molto sottile adiacente all'ala. Inoltre, alle basse velocità dei primi voli, l'aria può essere considerata incompressibile: il potenziale della velocità soddisfa quindi l'equazione di Laplace e il problema matematico diventa un problema di potenziale bidimensionale che può essere affrontato coi metodi delle funzioni di variabile complessa. Naturalmente può esistere una circuitazione non nulla attorno all'ala, perché la regione del piano in cui si ha il flusso non è semplicemente connessa. La teoria consiste di tre parti principali: 1) il teorema di Žukovskij (v. sotto) che dà la portanza (la componente della forza sull'ala perpendicolare alla direzione del moto) in funzione della circuitazione; 2) il principio di Kutta-Žukovskij-Chaplygin mediante il quale si determina la circuitazione sulla base di condizioni di flusso regolare sul bordo posteriore dell'ala; 3) varie rappresentazioni conformi che permettono di calcolare la circuitazione, e quindi la portanza, per sezioni alari di varie forme.

a) Il teorema di Žukovskij.

Nella fig. 2 la zona tratteggiata rappresenta l'intersezione di un'ala con un piano perpendicolare al suo asse (il piano z=x+iy). Se u e v sono le componenti secondo x e y rispettivamente della velocità dell'aria in un sistema in cui l'ala è a riposo, allora w=u−iv è una funzione analitica di z nella parte del piano esterna all'area tratteggiata, sotto le ipotesi che abbian~o fatto che il flusso sia incompressibile e irrotazionale. La circuitazione lungo una curva chiusa C è Γ=∫_C(u dx+v dy): essa è uguale alla parte reale di §_Cwdz; la parte immaginaria di questo integrale è nulla, perché è uguale al flusso di aria entrante attraverso C. La teoria delle funzioni complesse ci dice che il valore dell'integrale è lo stesso se computato su una qualunque curva C che faccia un solo giro attorno all'ala. Se la velocità dell'aria a grandi distanze ha componenti u=U e v=0, lo sviluppo di Laurent di w fornisce

poiché l'integrale §wdz, calcolato lungo C percorsa in senso orario, è −2πi volte il coefficiente di 1/z dello sviluppo. Per la legge di Bernoulli, la pressione è p=p₀−½ρ(u²+v²) e un calcolo diretto mostra che la forza risultante esercitata su di un'ala da questa pressione (portanza) è nella direzione +y, per Γ>0, ed è uguale in modulo a

F_y=ρUΓL=portanza, (23)

in cui L è là lunghezza dell'ala nella direzione perpendicolare al piano z. L'equazione (23) è il risultato del teorema di Žukovskij.

Il calcolo menzionato sopra si effettua come segue: supponiamo che il sistema sia in equilibrio, così che F_y sia bilanciata dal peso dell'aeromobile. Consideriamo l'aria contenuta in una colonna cilindrica la cui superficie interseca il piano z secondo una circonferenza di raggio ∣z∣=R, sufficientemente grande da contenere l'ala nel suo interno. La forza risultante esercitata dalla pressione sull'aria di questa colonna è pure uguale a F_y, perché il peso dell'aria è trascurabile (ed è in ogni caso esattamente bilanciato da una leggera diminuzione della pressione atmosferica p₀ con l'altezza); poiché la quantità di moto totale di quest'aria è costante nel tempo, la forza esterna che si esercita sulla colonna d'aria è uguale alla forza esercitata dall'aria sull'ala. Per le componenti della velocità su ∣z∣=R (con z=Re^iϑ) si ottiene dalla (22):

dove i puntini stanno per i termini in sen kϑ e cos kϑ, con k=2, 3, ... Le componenti x e y della forza sulla colonna cilindrica, per unità di lunghezza, si calcolano integrando il termine della pressione −½ρ(u²+v²) sulla superficie, moltiplicato per −dy e per dx, rispettivamente. Facendo uso della (24) si trova che l'unico contributo non nullo è dato dal prodotto dei primi due termini dello sviluppo di u, integrati rispetto a y, e che:

come detto sopra.

b) Esempio: il flusso attorno a un'ala di Žukovskij.

Attraverso successive modifiche e usando i metodi delle funzioni di variabile complessa, il flusso uniforme (bidimensionale, non viscoso, incompressibile e stazionario) attorno a una lamina piatta, mostrato nel primo disegno della fig. 3, è trasformato nel flusso attorno al profilo rappresentato nell'ultimo disegno. La coordinata complessa x+iy è indicata con z, z′, w e w′ nei vari piani, il potenziale complesso è indicato con ϕ+iψ in ogni caso.

All'inizio l'equazione ϕ+iψ=Aw′, con A>0, dà un flusso uniforme nella parte destra del piano w′. Poi la trasformazione rappresentata da

ci dà il flusso attorno a un cilindro circolare con i punti di ristagno a z′=±1. (È stato effettuato un taglio da +1 a −1 nei piano w′ e l'argomento della radice quadrata nella trasformazione è stato scelto in modo che il piano w′ venga rappresentato nella parte del piano z′ esterna al cerchio unitario). Successivamente si modifica il flusso aggiungendola circuitazione attorno al cilindro; allora

I punti di ristagno, cioè i punti in cui la velocità è nulla, sono dati da

le loro coordinate sono quindi:

Si effettua quindi una trasformazione lineare:

(α è una costante reale) che ingrandisce e sposta il cilindro, ma in modo che il suo contorno passi ancora per il punto z=1. Per il resto questa trasformazione lascia inalterato il carattere generale del flusso, facendo ruotare però tutto il sistema di un angolo α. La relazione B=A sen α che verrà stabilita qui sotto porta il punto posteriore di ristagno in z=1.

Infine l'inversa della prima trasformazione manda il nuovo cerchio nel profilo di Žukovskij:

(È stata tralasciata una costante additiva). Il significato delle costanti che appaiono in questa formula è il seguente: 1) la forma del profilo è determinata dai due parametri Re(z₀) e Im(z₀); 2) la velocità a grandi distanze, data da

ha modulo U=A∣1−z₀∣^-1 e forma un angolo α+arg (1−z₀) con l'orizzontale: α è perciò determinato dall'angolo d'attacco dell'ala; 3) la costante B è determinata dal principio di Kutta-Žukovskij-Chaplygin secondo cui la velocità deve essere finita al bordo d'uscita, cioè per w=1. La velocità è data dall'espressione:

nella quale il primo fattore tende a infinito per w che tende a 1; quindi deve essere

a z=1 e questo succede per B=A sen α, come già detto. La circuitazione su una curva chiusa percorsa in senso orario che racchiuda il profilo è Γ=2πB=2πA sen α; quindi il teorema di Z̆ukovskij dà per la portanza:

per unità di lunghezza dell'ala nella direzione perpendicolare al piano del disegno.

c) Ulteriori considerazioni.

Lo sviluppo successivo della teoria dell'ala in aeronautica è stato molto ampio; qui dobbiamo accontentarci di alcune brevi considerazioni.

Uno svantaggio del profilo di Žukovskij è la presenza di una cuspide al bordo d'uscita. Un profilo più soddisfacente, dal punto di vista della struttura, dovrebbe avere le tangenti al bordo d'uscita che s'incontrano con un angolo piccolo, ma diverso da zero. Profili di questo tipo sono stati ottenuti nel 1921 da von Kàrmàn e Trefftz con una modifica alle trasformazioni conformi descritte sopra, in cui l'esponente 0,5, corrispondente ai segni di radice nelle equazioni (25) e (26), è sostituito da un esponente leggermente maggiore.

Sono state apportate ulteriori modifiche al profilo per vari scopi, per esempio per arretrare il punto di minima pressione sul dorso e quindi il punto di distacco dello strato limite, quando aumenta l'angolo d'attacco.

La lunghezza, o apertura, finita di un'ala reale introduce vari effetti tridimensionali. Per un flusso strettamente bidimensionale, in base al teorema di Žukovskij, la resistenza (cioè la componente della forza sull'ala nella direzione del moto: −F_x nella notazione del È a) è nulla. In quest'approssimazione non viene spesa potenza per il volo a quota fissa, oltre a quella necessaria per vincere l'attrito di superficie. Non viene lasciata energia cinetica nell'aria dopo l'attraversamento dell'ala. Dato che la regione di flusso non è semplicemente connessa, la circuitazione Γ è effettivamente confinata nella zona attorno al profilo ed è detta vortice aderente. Per un'ala di apertura finita, la regione di flusso è semplicemente connessa e il vortice aderente continua oltre l'estremità dell'ala, dove è deviato bruscamente nella direzione della corrente sotto forma di vortice libero di scia. Pertanto la scia di un aereo consiste di due vortici orizzontali, ognuno proveniente dalla prossimità di un'estremità alare, rotanti in senso opposto in modo che l'aria tra di essi sia spinta verso il basso nella cosiddetta deflessione delle ali. Per fornire l'energia cinetica che in tale modo viene ceduta all'aria, è necessario un consumo di energia: corrispondentemente, si esercita una forza di rallentamento sull'ala.

Per alte velocità subsoniche (numeri di Mach maggiori di circa 0,75), il flusso può essere supersonico in regioni immediatamente al di sopra e immediatamente al di sotto del centro dell'ala; in questo caso il flusso si dice transonico. La prima volta che si trattò teoricamente questa situazione, si palesò una difficoltà matematica: si trovò che le equazioni del flusso non avevano soluzione (più precisamente, non avevano soluzioni continue, come si constatò in seguito) per la maggior parte dei profili. Morawetz dimostrò nel 1956 che, se esiste una soluzione per un profilo particolare, qualsiasi piccolo cambiamento nella forma del profilo nella regione supersonica porta a una forma per cui non esiste una soluzione continua. Ne segue che il flusso transonico è generalmente accompagnato da onde d'urto, che si possono vedere nelle strioscopie staccarsi dalle superfici inferiore e superiore posteriormente alla regione supersonica ed estendersi fino a distanze finite sopra e sotto il profilo, come si vede schematicamente nella fig. 4.

Nel volo supersonico generalmente molte perturbazioni si originano in varie parti dell'ala e della fusoliera e si estendono all'infinito. Il caso di un urto staccato, davanti a un corpo ogivale, è menzionato nel cap. 10.

4. Teorie statistiche della turbolenza.

La caratteristica essenziale del flusso turbolento è l'estrema irregolarità. La conoscenza del flusso in un intorno I₁ del punto x₁, t₁ dello spazio-tempo non dà praticamente informazioni sul flusso in un intorno I₂ del punto x₂, t₂, a meno che i due intorni non siano molto piccoli e molto vicini l'uno all'altro. Fintanto che si può descrivere il flusso come una sovrapposizione di vortici (per fare questo quantitativamente bisognerebbe dare una definizione precisa di vortice, ma qui ci occupiamo solo degli aspetti qualitativi di una descrizione di questo tipo), debbono essere presi in considerazione moltissimi vortici di dimensioni molto diverse. Una turbolenza pienamente sviluppata in una certa regione può infatti essere definita come un flusso in cui vi sia un numero considerevole di vortici con diametri compresi tra l₁ e l₀, con l₀≪l₁≪L, dove L è una dimensione caratteristica della regione. Se l₀≈1 mm, come può accadere per esempio nel flusso a valle di una grata in una galleria aerodinamica, allora ci sono circa 10⁹ vortici in ogni metro cubo di aria. Questo fatto porta a pensare che si possano definire le caratteristiche generali di un simile flusso mediante metodi statistici, proprio come le proprietà termodinamiche di un gas sono definite da un trattamento statistico del moto delle sue molecole. Il primo progresso rilevante in questa direzione fu fatto da G. I. Taylor nel 1935; oggi, quasi quarant'anni dopo, è chiaro che la teoria statistica della turbolenza sta diventando molto più difficile della teoria statistica dei moti molecolari. Alcune considerazioni sui motivi di questa differenza sono dati qui sotto. L'attuale teoria, incompleta, consiste in un insieme di relazioni tra funzioni che descrivono varie correlazioni e varie distribuzioni spettrali. Se è nota una di queste funzioni, da essa se ne possono derivare altre; attualmente però non abbiamo modo di determinare la prima funzione per un dato problema fisico, se non mediante misure o argomentazioni sull'ordine di grandezza, come i metodi di lunghezze di mescolamento; spesso questi metodi sono utili, ma sono molto approssimativi e generalmente danno affidamento solo dopo che siano stati confrontati con l'esperienza. Tuttavia le relazioni tra funzioni, cui abbiamo accennato sopra, sono basate su metodi statistici validi (e sono in ottimo accordo con l'esperienza); nel futuro entreranno certamente a far parte di una teoria completa.

a) Il tensore degli sforzi di Reynolds.

A volte è sufficiente conoscere alcune proprietà medie del moto turbolento. Supponiamo che il campo di velocità v=v(x, t) possa essere scritto v=U+u, dove U rappresenta il flusso medio variabile solo di poco su distanze e tempi paragonabili ai diametri e alle vite dei singoli vortici, mentre u rappresenta la turbolenza stessa, la cui media si annulla su distanze e tempi relativamente grandi. Se g=g(x, t) è una qualunque quantità dipendente dal campo u, allora à=à(x, t) rappresenta la media di g su un intervallo di tempo (t−Δt, t+Δt), che si suppone lungo rispetto ai tempi di variazione dei singoli vortici, ma breve rispetto a quelli del moto medio. Se u_j(j=1, 2, 3) sono le componenti di u, le medie ū_j sono tutte nulle, mentre le medie del tipo -u-_j-u-_k sono, in genere, diverse da zero.

Si suole anche far uso di medie spaziali o d'insieme, al posto delle medie temporali sopra descritte. Per le medie d'insieme, come nella meccanica statistica, si considera un insieme di molti sistemi fisici identici che differiscano solo per le condizioni iniziali, ottenute mediante una qualsiasi distribuzione casuale. I lavori teorici di C.C. Lin (v., 1955) e di M.S. Uberoi e S. Corrsin (v., 1953), insieme al lavoro sperimentale compiuto da numerosi ricercatori negli anni cinquanta, hanno mostrato che, in certe ipotesi restrittive, i tre metodi di media danno risultati quasi identici. Per una turbolenza omogenea, la media spaziale è chiaramente la più appropriata.

L'influenza della turbolenza sul flusso medio venne studiata da O. Reynolds nel 1895. Egli partì dall'equazione di Navier-Stokes per il flusso incompressibile, che può essere scritta nel modo seguente:

(perché Σ∂v_k/∂x_k=0). Se si sostituisce v con U+u, si effettuano le medie e si porta un termine al secondo membro, si ottiene:

Il tensore

τ_jk=−ρ-u-_j-u-_k, (30)

la cui divergenza appare nella (29), è chiamato tensore degli sforzi di Reynolds. In certe circostanze questo sforzo ha la stessa forma dello sforzo dovuto alla viscosità e si chiama perciò ‛viscosità di vortice', dato che deriva dal trasporto del momento dovuto ai vortici, nello stesso modo in cui la viscosità ordinaria, o molecolare, deriva dal trasporto del momento dovuto alle molecole. Nel flusso turbolento l'effetto della viscosità vorticosa domina quello della viscosità molecolare. Uno degli obiettivi primari del- la teoria statistica della turbolenza (che, per ora, non è assolutamente stato realizzato in pieno) è quello di poter determinare il tensore degli sforzi di Reynolds in certune condizioni particolari, come nel flusso di Poiseuille, nel flusso di Couette, in strati limite turbolenti, in getti che si allargano ecc. Similmente, nei problemi di convezione termica, si desidera conoscere il trasporto di calore da parte dei vortici.

b) Correlazioni.

La statistica di una velocità fluttuante v(x, t) può essere descritta in almeno due modi: 1) mediante la correlazione tra valori di v in punti vicini; 2) mediante la trasformata di Fourier di v rispetto ad x. Mostreremo che questi due metodi sono collegati tra di loro e che, in entrambi, le equazioni dinamiche forniscono informazioni sulla statistica delle fluttuazioni.

La maggior parte delle ricerche si è occupata del caso più semplice a trattarsi, di una turbolenza omogenea, incompressibile e isotropa, nell'intento di generalizzare i risultati, in un secondo tempo, a problemi di flusso più complessi; solo questo caso sarà discusso nel resto di questo paragrafo. Nei lavori di G. I. Taylor e di altri, compiuti tra il 1935 e il 1940, nei quali la teoria basata sulle correlazioni fu combinata con misure sperimentali, si trovò che una turbolenza isotropa e omogenea può essere prodotta con assai buona approssimazione in una galleria a vento da una grata posta trasversalmente, con una spaziatura della trama dell'ordine del centimetro. La velocità dell'aria a valle della grata può essere misurata con strumenti a filo caldo, nei quali la resistenza elettrica del filo è sensibile (in modo praticamente istantaneo, se il filo è molto fine) all'effetto raffreddante dell'aria, che è proporzionale alla sua velocità attorno al filo. Correlazioni, componenti di Fourier e simili possono quindi essere ottenute con un'opportuna strumentazione elettronica.

Per definire le correlazioni quadratiche (correlazioni di ordine superiore saranno discusse in seguito), sia u(x, t), come sopra, il campo turbolento dal quale è stato sottratto il flusso medio, che ora si pensa costante. Ovviamente, una turbolenza omogenea è necessariamente dipendente dal tempo, perché la viscosità fa diminuire, anche se lentamente, l'energia cinetica totale. Questo significa che, sebbene il flusso turbolento nella galleria sia quasi omogeneo, non lo può essere esattamente e lo smorzamento della turbolenza può essere seguito in un sistema di coordinate x che si muova lungo la galleria solidalmente col flusso medio. Siano x ed x′ due punti e poniamo r=x−x′. Il tensore di correlazione quadratica che connette questi due punti è

Per l'isotropia che abbiamo supposto, il campo u(x, t) è statisticamente invariante rispetto a rotazioni degli assi coordinati. Si può mostrare facilmente (come fu fatto per la prima volta da T. von Kàrmàn nel 1937 con un metodo diretto e da H.P. Robertson nel 1940 con un metodo che può essere esteso a correlazioni cubiche e di ordine superiore) che, per una turbolenza isotropica, questo tensore dev'essere dato dal prodotto di r_jr_k per una funzione di r e t sommato al prodotto di δ_jk per un'altra funzione simile, dove r=∣r∣. In corrispondenza, si definiscono due funzioni f e g scrivendo:

in cui -u-² o -u-²- (-t-) denota il valore quadratico medio di qualsiasi componente di u; -u-² è la stessa per tutte le componenti e non dipende da x, ma decresce col procedere del tempo. Dall'isotropia segue anche che f e g sono funzioni pari di r. Il significato fisico di f e g può essere visto prendendo r lungo uno degli assi coordinati, l'asse x₁ per esempio; in questo caso R₁₁=-u-²f(r, t), R₂₂=R₃₃=-u-²g(r, t); cioè f è il coefficiente di correlazione per due componenti di u parallele a r (quelle in x e in x′), mentre g è il coefficiente di correlazione per le analoghe componenti in una direzione normale a r. Per due componenti, una parallela e una normale a r, e per due componenti, entrambe normali a r e normali tra loro, la correlazione è nulla. Per r=0, f=g=1.

Dalla condizione di incompressibilità, scritta nella forma ∇•u=0 segue che le funzioni f e g sono legate dall'equazione

tutte le correlazioni quadratiche sono pertanto esprimibili in termini di una singola funzione scalare f(r, t). La relazione (33) è stata ottenuta da von Kármán nel 1937 e confermata sperimentalmente da D. C. Macphail nel 1940.

La quantità −ρR_jk(0, t) è il tensore di Reynolds; nel problema che stiamo trattando, tuttavia, essa rappresenta semplicemente una pressione costante e isotropa.

La disuguaglianza di Schwarz, scritta nella forma

mostra che

Un tensore del terz'ordine di correlazione cubica, in cui la dipendenza dal tempo sia stata eliminata, è dato da -u-_j- (-x-)- -u-_k- (-x-′-)-u-_l- (-x-″). Per semplificare la teoria, è sufficiente considerare il caso in cui due dei punti x, x′, x″ coincidono. In questo caso si ha ancora che tutte le correlazioni cubiche possono essere espresse mediante una sola funzione scalare h(r, t) che, quando il vettore r=(x′−x) giace nella direzione x₁, è la media -u-²-₂- (-x-)- -u-₁- - (-x-′-), normalizzata dividendola per (-u-²)^3/2. Ne risulta che h(r, t) è una funzione dispari di r e che il termine dominante della sua espansione in serie di Taylor è proporzionale a r³.

Adesso si può spiegare l'idea che sta dietro ai tentativi di basare una teoria della turbolenza sulle correlazioni. Il campo u(x, t) soddisfa l'equazione di Navier-Stokes (29) se si sostituisce v con u. La dividiamo per la densità costante ρ e introduciamo la cosiddetta viscosità cinematica ν=μ/ρ. Moltiplichiamo l'equazione risultante nel punto x per u_j(x, t): il primo termine sulla sinistra diviene u_j(x′, t) ∂/∂t[u_j(x, t)]. (Si noti che qui non si sta usando la convenzione sulla somma degli indici ripetuti, per cui l'espressione non s'intende sommata sull'indice j). Quindi, se sommiamo l'equazione corrispondente scambiando x con x′ e mediamo rispetto al tempo, secondo la (31), otteniamo ∂/∂t[R_jj(r, t)], che è uguale, per la (32), a ∂/∂t[-u-²f(r, t)]. Il contributo dell'ultimo termine a secondo membro della (28) può essere espresso, in modo analogo, in termini di f(r, t) e delle sue derivate rispetto a r. Dalle condizioni di isotropia e di incompressibilità segue che il contributo del termine contenente il gradiente della pressione è nullo. Il contributo del secondo termine, non lineare, al secondo membro contiene correlazioni triple, che possono essere espresse mediante la funzione h(r, t) e le sue derivate rispetto a r. L'equazione risultante,

fu ottenuta da von Kármán e Howarth nel 1938 e verificata sperimentalmente da Stewart nel 1951. Nonostante il difetto evidente di contenere due funzioni incognite f e h, da essa si possono trarre certe conclusioni riguardanti gli aspetti microscopici della turbolenza, generalmente con l'aiuto di ulteriori ipotesi.

In particolare, poiché f è una funzione pari di r il cui primo termine dell'espansione in serie di Taylor è uguale a 1, mentre h è una funzione dispari il cui primo termine è proporzionale a r³, si vede che ponendo r=0 nella (35) si ha:

dove λ si ricava da:

λ ha le dimensioni di una lunghezza e Taylor, che ottenne la (36) con un metodo più diretto nel 1938, la chiamò ‛scala di vorticità'. L'equazione mostra che l'energia cinetica per unità di massa, 3/-u-² 2, decresce col passare del tempo. Il risultato si può verificare sperimentalmente, perché λ può essere ottenuto da una curva sperimentale del coefficiente di correlazione f in funzione di r (v. Taylor, 1935).

Per tentare di superare la difficoltà della presenza di due incognite nella (35), si può ottenere un'equazione per la derivata temporale della funzione di correlazione dei terzo ordine h, moltiplicando l'equazione (28) di Navier-Stokes per il prodotto delle due componenti della velocità (entrambe in x′ o una in x e una in x′) e poi procedendo in modo analogo. Tuttavia, il risultato contiene correlazioni del quarto ordine provenienti dal termine non lineare della (28), per cui viene introdotta almeno una nuova funzione incognita. Il proseguimento di questo metodo porta a una successione infinita di equazioni a derivate parziali accoppiate. Sono stati fatti tentativi di troncare la successione dopo un numero finito di equazioni introducendo ipotesi o approssimazioni ulteriori, ma senza troppo successo. Se esistano, se cioè siano in numero finito, correlazioni di ordine arbitrariamente grande è un problema ancora insoluto.

c) Lo spettro dell'energia.

Cominciamo col considerare per prima l'analisi di Fourier di una componente di u rispetto a una componente di x, per un valore di t fissato. La funzione risultante, che chiameremo semplicemente u(x), non può essere sviluppata in serie di Fourier, perché non è periodica, né se ne può fare la trasformata di Fourier, perché le oscillazioni di u(x) non sono localizzate, in quanto si è supposto che la turbolenza sia omogenea e che pertanto si estenda all'infinito: quindi

non è finito. Per questo Taylor ricorse nel 1938 alla cosiddetta analisi di Fourier generalizzata, che era stata sviluppata da N. Wiener nel 1925 proprio per il caso di fenomeni fisici come la turbolenza e la luce bianca. (Da allora la generalizzazione è molto progredita, nell'ambito della teoria delle distribuzioni). L'analisi di Wiener contiene le serie e gli integrali di Fourier come casi particolari, oltre all'analisi armonica delle funzioni quasi periodiche di H. Bohr (v., 1924), ma è più generale di una semplice unione di questi tre tipi di analisi; ha, in effetti, proprio il grado di generalità necessario per i fenomeni fisici in questione.

Per ragioni di praticità, sono consigliabili le serie di Fourier, che useremo nel paragrafo seguente. E intuitiva- mente evidente che, se i fenomeni sono resi artificialmente periodici su distanze o tempi molto lunghi, in generale le correlazioni a grande distanza così introdotte non hanno effetto. Tuttavia, per una chiara comprensione è essenziale, come Taylor riconobbe, formulare l'argomento nei termini dell'analisi di Fourier generalizzata.

Nell'analisi di Wiener di una funzione u(x), non necessariamente a valori reali, si suppone solo che esista, per ogni valore di r, la funzione di correlazione

in questa espressione l'asterisco denota il complesso coniugato e la barra la media rispetto a x. L'energia cinetica per unità di massa mediata su tutte le x è ½R(0). Segue dalla (38), con un breve calcolo in cui si fa uso della disuguaglianza di Schwarz, che ∣R(r)∣≤R(0): quindi R(r) è, per lo meno, limitata. Nel caso della turbolenza, R(r)→0 per r→∞ e, come si vedrà, la distribuzione spettrale dell'energia è data dalla trasformata di Fourier di R(r).

In questo caso, come nella maggior parte dei problemi fisici, si fa l'ulteriore ipotesi che u(x) e R(r) siano funzioni continue. (Wiener cita l'esempio curioso in cui, se u(x)=sen x², R(r) non è continua per r=0. Evidentemente la condizione, fisicamente plausibile, della continuità di R(r) esclude le rapide oscillazioni della funzione u(x) all'infinito quali si riscontrano in sen x²).

Con le ipotesi dette sopra si può così definire una funzione

la quale è una specie di trasformata di Fourier integrata di u(x). In effetti, se la derivata σ′(k) di σ(k) è a quadrato sommabile (il che può avvenire solo se u(x) è anch'essa a quadrato sommabile), allora σ′(k) è la trasformata di Fourier ordinaria, come si può vedere differenziando la (39) rispetto a k. Nell'altro caso limite, se σ(k) è una funzione a gradini, con gradini uniformemente spaziati, u(x) è data da una serie di Fourier. Più in generale, se σ(k) è una funzione a variazione totale limitata, u(x) è data da un integrale di Stieltjes:

(questa formula è valida sia per gli integrali, sia per le serie di Fourier). Tuttavia, quando u(x) è una funzione del tipo di quelle che appaiono nelle turbolenze, σ(k) non ha una variazione limitata nemmeno localmente (se l'avesse, infatti, l'energia cinetica media R(0) sarebbe nulla), quindi la formula d'inversione, di cui fortunatamente non v'è necessità nella teoria della turbolenza, è, per forza di cose, più complicata. Wiener ha dimostyato che σ(k) è a quadrato sommabile su ogni intervallo finito e, se I(k₀) è il risultato di una integrazione per parti di

allora u(x) è data dal limite di Cesàro di I(x, k₀):

La distribuzione spettrale dell'energia, rappresentata da u(x), è di interesse fondamentale. Se i rappresenta l'intervallo dei numeri d'onda compreso tra k₁ e k₂, si ha che

(da interpretarsi, in modo analogo alla (40), come un'integrazione per parti formale) è il contributo alla funzione u(x) derivante da tutti i numeri d'onda k compresi nell'intervallo Δ. Wiener ha dimostrato che l'intensità ½-∣-u-_Δ- -(-x-)- -∣² di questo contributo, corrispondente all'energia cinetica per unità di massa, mediato su tutti i valori di x, è data da

½-∣-u-_Δ- - (-x-)--- -∣²=S(k₂)−S(k₁), (42)

dove si è posto

S(k) è la funzione di distribuzione spettrale integrata (o cumulativa) di u(x).

Si può osservare che lo spettro della turbolenza è continuo, cioè che S(k) è una funzione cosiddetta ‛assolutamente continua' e la sua derivata S′(k) è la funzione di densità spettrale. In generale, la regolarità di una trasformata di Fourier dipende dalla rapidità con cui la funzione originale (in questo caso la R(r)) va a zero al tendere di r all'infinito. Fisicamente, ci si aspetterebbe una correlazione molto piccola a grandi distanze. Batchelor e Proudman hanno dimostrato nel 1956 che normalmente, per una turbolenza omogenea, ci si può aspettare che R(r) decresca come o più rapidamente di r^-6 e questo è più che sufficiente per garantire l'esistenza di S′(k). (Non sarebbe così se u(x) fosse periodica o quasi periodica, dato che tali funzioni presentano forti correlazioni a grandi distanze e hanno spettri a righe).

Fino a questo punto la discussione è stata basata su di un modello unidimensionale. Nel caso tridimensionale la funzione di correlazione R(r) è sostituita dalla matrice di correlazione (31)

R_jk(r)=-u-_j- (-x-)- -u-_k- - (-x-+-r-),

nella quale ora gli argomenti sono vettori. L'estensione dell'analisi di Fourier generalizzata al caso tridimensionale è immediata. Per arrivare al risultato, si nota per prima cosa che le equazioni (42) e (43) possono essere riscritte nel modo seguente:

dove, come nel caso precedente, Δ rappresenta l'intervallo (k₁, k₂) e S è una funzione dell'intervallo. Sia adesso Δk un intervallo tridimensionale, cioè un parallelepipedo rettangolare nello spazio k, allora, per la j-esima componente di u, la (44) è sostituita da:

Per una turbolenza isotropa, Δk è sostituito dalla sfera B_k di raggio k nello spazio k; l'energia cinetica per unità di massa per tutti i vettori d'onda k di modulo minore o uguale a k è allora data da:

Per calcolare l'integrale di e^ik•r su B_k si fa uso dell'identità

Se si trascura la dipendenza temporale, gli elementi di matrice R_jj(r) sono dati dalla (32) in funzione di f(r) e g(r) e si ottiene per la funzione spettrale dell'energia l'espressione

Questa equazione stabilisce il legame tra le correlazioni spaziali e la distribuzione dell'energia in funzione dei numeri d'onda nel caso di una turbolenza isotropa. Come si è detto precedentemente, in generale si suppone che le funzioni f(r) e g(r) decrescano, per r tendente all'infinito, con rapidità sufficiente perché l'energia abbia uno spettro continuo o, più precisamente, secondo il linguaggio matematico, assolutamente continuo; lo spettro è allora caratterizzato dalla funzione di densità spettrale

F(k)=S′(k);

F(k)dk rappresenta l'energia per unità di massa relativa alle componenti di Fourier aventi numeri d'onda compresi nell'intervallo k, k+dk.

d) La cascata d'energia; l'intervallo inerziale e l'intervallo viscoso.

Lo sviluppo di Fourier del campo delle velocità sia rappresentato schematicamente dalla serie di Fourier seguente:

dove ???OUT-l??? rappresenta un reticolo cubico di punti nello spazio k. L'energia cinetica della componente con vettore d'onda k è proporzionale a ∥uk∥². Se il campo soddisfacesse le equazioni del moto linearizzate, l'energia sarebbe costante nel tempo, per ogni k, ma, a causa delle non linearità, l'energia può essere trasferitada una componente all'altra. Ciò suggerisce un'immagine della turbolenza in cui l'energia è distribuita tra un gran numero di componenti di Fourier e viene costantemente, e in certo modo casualmente, ridistribuita tra queste.

Se si è in condizioni di turbolenza pienamente sviluppata, cioè se le lunghezze d'onda cui corrispondono quantità apprezzabili di energia variano dalle lunghezze che caratterizzano il sistema fisico (aperture alari, diametro del condotto, spaziatura della griglia,...) fino a lunghezze molto più piccole, l'energia cinetica è fornita al sistema alle lunghezze d'onda più lunghe ed è sottratta dalla viscosità alle lunghezze d'onda più corte, per le quali, a pari velocità, esistono i gradienti maggiori. In corrispondenza a ogni lunghezza d'onda intermedia λ₀ c'è un trasferimento costante di energia, in media, dalle lunghezze d'onda maggiori di λ₀ a quelle minori di λ₀, pari a una certa quantità ε per unità di massa e di tempo. Questo trasferimento è detto ‛cascata d'energia'.

Incidentalmente, si noti che la cascata d'energia è un effetto tridimensionale che non si verifica in un flusso bidimensionale, per quanto irregolare, a causa della conservavazione della vorticità ω=∇•u; in questo senso, la turbolenza bidimensionale non esiste. Se si considera la rotazione della seconda delle equazioni (11), per un valore di ρ costante, si ottiene l'equazione di Helmholtz

in cui è stata trascurata la viscosità, per ragioni che diremo in seguito. L'ultimo termine del primo membro si annulla nel caso di un flusso bidimensionale, poiché, se x e y sono le coordinate sul piano del flusso, ω è nella direzione z, mentre le componenti di u sono indipendenti da z. Questo mostra che la vorticità

ω=ω_z=∥ω∥=∂v/∂x−∂u/∂y

è costante nel tempo per ciascuna particella. Se moltiplichiamo scalarmente l'equazione risultante per 2ω, troviamo che

(∂/∂t+u•∇)ω²=0.

Poiché è ∇•u=0 per un flusso incompressibile, questa equazione può anche essere scritta nella forma:

∂ω²/∂t+∇•(ω²u)=0.

Integrando sul volume di una cella cubica, uguale al periodo del campo (46), si vede che per un flusso bidimensionale si ha

L'energia cinetica per unità di volume, sia per il caso di un flusso bidimensionale sia per il caso tridimensionale, è proporzionale a

∫∥u∥²dτ,

cioè a

Σ_(k)∥u_k∥², (48)

mentre il quadrato della vorticità per unità di volume è proporzionale a

∫∥ω∥²dτ,

cioè a

Σ_(k)∥k⋀u_k∥²=Σ_(k)∥k_k∥²∥u_k∥², (49)

in cui nell'ultimo passaggio si è fatto uso della k•u_k =0, che segue dall'equazione ∇•u=0.

Si supponga adesso che una certa quantità di energia sia fornita istantaneamente alle componenti con grande lunghezza d'onda (k piccolo) e che il sistema sia poi lasciato indisturbato. Non tenendo conto della viscosità, che è trascurabile fintanto che le componenti di lunghezza d'onda molto piccola non contengono energia apprezzabile, la quantità (48) è costante. Per un flusso bidimensionale anche la (49) è costante; quindi il valore medio del modulo di k non può crescere col tempo e le componenti di piccola lunghezza d'onda non vengono eccitate. Il flusso di energia 8 è quindi nullo in questo caso.

Nel caso tridimensionale si suppone ora che ci siano un numero d'onda k₀ e una corrispondente lunghezza d'onda λ₀ tali che: 1) l'energia sia fornita al sistema (da eliche o simili) prevalentemente solo a lunghezze d'onda maggiori di λ₀; 2) il moto sia statisticamente isotropo (in un sistema di riferimento in cui la velocità media sia nulla) per tutte le lunghezze d'onda minori di λ₀. Dietro alla seconda ipotesi c'è l'idea che, se λ₀ è notevolmente inferiore alle lunghezze d'onda a cui viene fornita la maggior parte dell'energia, l'effetto dei trasferimenti di energia quasi casuali dalle componenti di Fourier con λ molto maggiore di λ₀ a quelle con λ minori di λ₀ tenda a far sì che il moto diventi isotropo. In tal caso, l'intera struttura della turbolenza nella cosiddetta gamma universale di numeri d'onda k>k₀(λ〈λ₀) dovrebbe essere completamente determinata dai parametri e (velocità di trasferimento dell'energia nella cascata) e i' (viscosità cinematica). Quantità derivate da ε e ν aventi le dimensioni di una lunghezza e di una velocità sono:

l₁=ν^3/4ε^-1/4, v₁=(νε)^1/4. (50)

Un numero di Reynolds appropriato al problema è

Per una turbolenza pienamente sviluppata deve essere R≫1, come supporremo qui.

Il carattere generale della turbolenza nella gamma universale è determinato da considerazioni dimensionali. Per esempio, se u e u′ sono le velocità in punti separati da una distanza r, se cioè u=u(x) e u′=u(x′) con ∥x−x′∥=r, allora

-∥-u-′-∥-²=v²₁β(r/l₁)=(νε)^1/2β(ε^1/4r/ν^3/4), (52)

in cui β è una funzione universale.

Il primo membro dell'equazione precedente può essere scritto come somma di tre termini, a seconda che u e u′ siano paralleli o perpendicolari al vettore x−x′ che congiunge i due punti. Sia x′−x nella direzione x₁, così che le sue componenti siano r, 0, 0. Allora, nel caso parallelo, in base alle (31) e (32), si ha:

dove β_∥ è un'altra funzione universale. Nel caso perpendicolare si ha, invece:

Dato che il primo membro della (52) è

risulta che β=β_∥+2β_⊥.

Per una gamma di numeri d'onda compresi tra k₀ e un valore di poco inferiore a k₁=2π/l₁, chiamata ‛intervallo inerziale', le forze viscose sono trascurabili e i secondi membri delle equazioni (52) (53) e (54) non dipendono da ν. Questo implica che le funzioni β(r/l₁), β_∥(r/l₁) e β_⊥ (r/l₁) sono tutte del tipo cost×(r/l₁)^2/3; quindi ∥u−u′∥², ecc., sono proporzionali a (εr)^2/3. La relazione (33) tra g ed f mostra che β_⊥=4/3β_∥ nell'intervallo inerziale.

La funzione spettrale F(k)=S′(k) per l'intervallo inerziale può essere derivata sia dalla (45), sia da un ragionamento dimensionale molto più semplice; infatti, l'unica combinazione di ε e k dimensionalmente corretta è

F(k)=cost×ε^2/3k^-5/3. (55)

Le idee e i risultati riguardanti l'intervallo inerziale sono stati attribuiti a molti, ma principalmente a Kolmogorov, Taylor e Obuchov.

Per determinare le funzioni universali β, β_∥ e β_⊥, sarebbe necessario conoscerle nella regione viscosa k≫k₁ e nella zona di transizione k≃k₁ (nella quale le forze viscose e inerziali sono confrontabili). Finora non si è giunti a questo, sebbene siano stati fatti numerosi tentativi, basati su varie ipotesi alquanto arbitrarie.

Una determinazione sperimentale delle funzioni universali è stata ostacolata dal fatto che il numero di Reynolds (51) generalmente è troppo piccolo, anche nelle grandi gallerie a vento, perché possa stabilirsi una zona inerziale ben sviluppata. Si è fatto di recente qualche progresso, dovuto a misure effettuate nell'atmosfera, dove sono comuni numeri di Reynolds molto più grandi.

Recentemente sono stati espressi dei dubbi sulla validità dell'ipotesi, implicitamente fatta sopra, che la velocità ε di trasferimento dell'energia possa essere considerata alla stregua di un parametro costante, piuttosto che come una quantità essa stessa soggetta a fluttuazioni nello spazio e nel tempo. Non è nota la misura entro cui queste fluttuazioni potrebbero modificare i risultati precedenti, in particolare l'esponente 5/3 nella (55).

e) Distanza di mescolamento.

Consideriamo dapprima un flusso a strati piani e paralleli, come per esempio in uno strato limite, in cui la velocità media nella direzione x sia ū(y). Se il flusso è turbolento si suppone che gli elementi di fluido si muovano, in media, per una certa distanza prima di perdere il loro momento, mescolandosi con il fluido circostante. La componente x della velocità dell'elemento è, in media, ū(y₁) se si origina alla quota y₁; se si mescola col fluido circostante alla quota y₂, trasferisce al fluido una quantità di moto proporzionale a ū(y₂)−ū(y₁)≃(y₂−y₁)dū/dy, proprio come una molecola di gas cede una corrispondente quantità di moto in una collisione dopo aver viaggiato per un tratto eguale al cammino libero medio. In base a questa analogia si deduce (v. Monin e Yaglom, 1971) che la componente x, y del tensore di Reynolds è data da

dove l, detta ‛distanza di mescolamento', è una quantità dell'ordine della distanza media percorsa da un elemento di fluido. In generale, l deve essere considerata una funzione di y (per esempio, se c'è una parete rigida in y=0, allora l(y)→0, per y→0). Se fosse nota la funzione l(y), la (56) costituirebbe un'equazione differenziale per la velocità media di flusso ū(y), perché (∂/∂y)τ_xy è determinato dalle componenti x del gradiente di pressione e delle forze di volume che agiscono sul fluido.

Nella (56) la dipendenza quadratica da dū/dy, al posto della dipendenza lineare che si ha per la viscosità molecolare, sorge perché la velocità trasversale media dell'elemento di fluido è proporzionale a l∣dū/dy∣, mentre la velocità media trasversale di una molecola di un gas dipende solo dalla temperatura.

Formule analoghe basate su lunghezze di mescolamento sono usate spesso per il calcolo del trasporto del calore mediante convezione turbolenta e nel caso del trasporto di una sostanza che si sta mescolando con altre.

Espressioni per l'ordine di grandezza di l(y) sono state date da von Kármán e altri: questi metodi sono stati molto utili per capire qualitativamente vari fenomeni, ma devono essere considerati come assolutamente provvisori.

5. Strati limite.

a) Strato limite sopra una lamina piana.

Quando un corpo di forma aerodinamica si muove attraverso aria o acqua calma a un elevato numero di Reynolds, il flusso è uguale, con ottima approssimazione, a quello che si avrebbe in assenza di viscosità, eccezion fatta per un sottile strato limite adiacente al corpo, per una circolazione diversa da zero attorno al corpo, come nella teoria dell'ala di Žukovskij, e per ciò che avviene nella scia, dove possono esserci turbolenza e vortici. Supporremo che il flusso sia sufficientemente subsonico perché il fluido possa essere considerato incompressibile. (Per una discussione dell'influenza della compressibilità a velocità superiori, compresi il flusso transonico e supersonico, v. Schlichting, 1960⁶). Lo strato limite determina la resistenza superficiale d'attrito e il fenomeno del distacco dello strato limite è responsabile dello stallo delle ali e della grande resistenza incontrata dai corpi non aerodinamici.

La comprensione del concetto di strato limite incominciò con il lavoro di L. Prandtl nel 1904 e di H. Blasius nel 1908 e da allora si è notevolmente accresciuta in seguito a lavori sia teorici sia sperimentali. Qui cercheremo solo di descrivere i concetti fisici fondamentali in alcuni semplici casi.

Normalmente lo strato limite è laminare sulla parte frontale del corpo, ma può diventare turbolento molto più a valle. Consideriamo prima il flusso stazionario parallelo a una sottile lamina che occupa il semipiano x≥0, y=0, come è rappresentato nella fig. 5. Lo spessore dello strato limite sia δ=δ(x). (Naturalmente lo spessore non è definito con precisione, perché c'è soltanto una transizione graduale tra lo strato limite e il flusso esterno; ma qui è necessario solo per discussioni sugli ordini di grandezza). La teoria suppone che la viscosità cinematica ν=μ/ρ sia molto piccola, che δ→0 per ν→0, per un valore di x fissato, e che ci si possa fermare ai termini del più basso ordine in ν (e quindi in δ) nell'equazione di Navier-Stokes. Siano u e v le componenti x e y della velocità. Al di fuori dello strato limite, la velocità u è eguale a una costante positiva U e v=0. Sulla lamina (y=0, x>0): u=v=0. Si suppone che u, ∂u/∂x, ∂²u/∂x², ∂p/∂x siano limitati (cioè di ordine 1:O(1)) per ν→0. Integrando l'equazione di continuità, ∂u/∂x+∂v/∂y=0, rispetto alla y, partendo da y=0, si vede che v è al massimo dell'ordine O(δ) su tutto lo strato limite. Dato che u cresce da zero a U attraverso lo strato, ∂u/∂y è d'ordine O(δ^-1) e ∂²u/∂y² è dell'ordine O(δ^-2). Quindi i termini della prima equazione di Navier-Stokes hanno gli ordini di grandezza indicati nella riga sottostante l'equazione:

Evidentemente il termine ν∂²u/∂x² può essere trascurato. Dato che lo strato limite è, per definizione, la regione in cui il termine di viscosità è paragonabile agli altri termini, δ deve essere dell'ordine O(ν^1/2) per ν→0. La seconda equazione di Navier-Stokes

indica allora che ∂p/∂y è dell'ordine O(δ) e quindi che p non dipende da y entro termini dell'ordine O(δ²). Arriviamo così al sistema seguente:

u=v=0 per y=0, x>0, (59)

(u, v)→(U, 0) per y→∞. (60)

È sufficiente prendere in considerazione la regione y≥0. Nel nostro caso, essendo p costante nel flusso esterno, il termine in dp/dx è nullo: nella (57) esso è stato scritto perché sarà utile in un problema modificato.

Alle equazioni precedenti è applicabile un principio di similitudine dinamica, sul tipo del principio associato al numero di Reynolds. Supponiamo che u(x, y), v(x, y) sia una soluzione e che sia a una costante positiva. In questo caso le funzioni ú e ???37??? date da

ú(x, y)=u(ax, √-ay), ???37???(x, y)=√-av(ax, √-ay)

sono un'altra soluzione dello stesso problema, come si può controllare sostituendo ú e ???37??? nelle equazioni (57-60) e ricordandosi che dp/dx=0. Generalmente si fa l'ipotesi che la soluzione del problema sia unica; questo implica che ú=u, ???37???=v, cioè, in particolare, che

u(ax, √-ay)=u(x, y). (61)

Recentemente il lavoro di Olejnik, discusso brevemente qui sotto, ha dato la dimostrazione matematica dell'esistenza e unicità della soluzione. Poiché la (61) è valida per ogni x, y e a, essa in particolare è valida per a=1/x; quindi:

cioè u dipende da x e y solo attraverso il rapporto y/√-x. L'andamento della velocità, cioè il grafico di u in funzione di y attraverso lo strato, è lo stesso per ogni x, a parte un opportuno fattore di scala variabile secondo il valore di y. Ne segue che lo spessore δ dello strato limite cresce proporzionalmente a √-x lungo la lamina. E consuetudine introdurre la variabile adimensionale indipendente η e una funzione f mediante le equazioni

dove ψ è la corrente (∂ψ/∂y=u; ∂ψ/∂x=−v); f è quindi una funzione universale che soddisfa le equazioni

2f‴+ff″=0, f=f′=0 per η=0, f′(∞)=1, (63)

che seguono dalle (57), (59) e (60).

La funzione f è stata calcolata, risolvendo il sistema (63), da vari autori, a cominciare da Blasius nel 1908; risultati accurati sono stati ottenuti da L. Howarth (v., 1938). L'andamento della velocità è dato da u(x, y)/U=f′(η); un grafico di questa funzione è rappresentato nella fig. 6. La teoria è in ottimo accordo con le misure, molto accurate, di J. Nikuradse (v., 1942; v. Schlichting, 1960⁶, cap. VII). Per η=2,5 la velocità u è salita da zero, quanto valeva per η=0 (y=0 per un valore di x fissato), al 75% della velocità del flusso libero U; per η=5 ha raggiunto il 99% di U. La (62) indica quindi che possiamo prendere per lo spessore dello strato

dove η₀ è una costante il cui ordine di grandezza è compreso tra 2 e 5.

Dal momento che in questa formulazione manca un parametro avente le dimensioni di una lunghezza, non esiste un numero di Reynolds caratteristico per questo problema; esiste piuttosto un numero di Reynolds locale, Uδ/ν, che cresce come √-x lungo la lamina da 0, per x=0, all'infinito, per x=∞. Di conseguenza, le equazioni (57-60) non sono esatte in prossimità del bordo d'attacco della lamina; precisamente, l'equazione per v corrispondente alla (61) per u, risulta:

Se facciamo tendere x a 0 mantenendo costante il rapporto y/√-x, vediamo che per valori di x molto piccoli la soluzione è incompatibile con l'ipotesi che sia v≪U(v=O(δ)), su cui erano state fondate le equazioni. Non è quindi accettabile la soluzione per valori di x compresi tra 0 e il punto in cui x e δ(x) diventano paragonabili, cioè in una striscia lungo il bordo anteriore di spessore eguale ad alcuni multipli di ν/U. All'altro estremo, ci si deve aspettare che il flusso diventi turbolento, per x sufficientemente grande, per via dell'aumento del numero di Reynolds.

b) Strato limite su una superficie curva.

Le equazioni (57-60) possono essere usate anche per uno strato limite lungo una parete curva, o cilindrica, se la curvatura è blanda e se U e p sono opportune funzioni di x. In questo caso, x e y sono coordinate curvilinee che crescono, rispettivamente, nelle direzioni parallela e perpendicolare alla parete; la parete si trova in y=0; U(x) e p(x) sono la velocità e la pressione del flusso libero subito al di fuori dello strato limite. Questa conclusione fu derivata da Toilmien nel 1931 scrivendo le equazioni di Navier-Stokes in coordinate curvilinee e usando essenzialmente lo stesso ragionamento di prima sugli ordini di grandezza. E evidente che se lo spessore dello strato limite è ovunque molto piccolo rispetto al raggio di curvatura, le coordinate x e y possono essere considerate localmente quasi cartesiane, all'interno dello strato sottile. L'unica differenza sta nel fatto che adesso dp/dy è dell'ordine O(1), anziché O(δ), a causa delle forze centrifughe; ma la variazione di p attraverso lo strato può ancora essere trascurata (in quanto in tal caso è dell'ordine O(δ) anziché O(δ²)). Il flusso non può più essere espresso in termini di un'unica funzione universale, come nell'equazione (33), ma sono stati escogitati numerosi metodi di calcolo numerico, di sviluppo in serie e di approssimazioni analitiche per calcolarlo. Per prima cosa è necessario trovare U(x) e p(x) risolvendo il problema del flusso non viscoso. Quando si presenta il distacco dello strato limite, come per il caso di un cilindro o per il caso di un'ala in condizioni di stallo, il flusso esterno non è più irrotazionale, anche se è stazionario, e il calcolo di U(x) e p(x) diventa difficile.

L'idea del metodo della serie di potenze fu concepita da Blasius nel 1908 e da Hiemenz nel 1911 ed è stata perfezionata da Howarth nel 1935. Si suppone che il flusso esterno sia rappresentato da una serie di potenze:

in cui U₁, U₃, ... sono costanti ed l è una lunghezza caratteristica, come il raggio di curvatura del corpo nel punto di ristagno. Si è supposto che la x sia misurata a partire dal punto di ristagno anteriore per il flusso attorno a un cilindro o a un'ala col bordo d'entrata arrotondato, così che U(0)=0. Si è anche supposto che il corpo sia simmetrico rispetto a un piano parallelo alla direzione del flusso all'infinito, altrimenti andrebbero incluse potenze pari di x. p(x) si può ottenere da U(x) mediante la legge di Bernoulli, per la quale p+½ρU²=p₀. La corrente per il flusso nello strato limite assume allora la forma

in cui

è uguale alla y, espressa in termini di un'unità di lunghezza paragonabile allo spessore dello strato limite. Le funzioni F_2n+1 si calcolano sostituendo ∂ψ/∂y e −∂ψ/∂x a u e v nella (57), uguagliando a zero il coefficiente di ogni potenza di x e risolvendo poi le equazioni differenziali ordinarie. Howarth ha dimostrato che F₁ è una funzione universale di η, F₃ è una funzione universale moltiplicata per U₃/U₁, F₅ può essere espressa in termini di U₁, U₃, U₅ e di due funzioni universali, F₇ in termini di U₁,..., U₇ e di tre funzioni universali, e così via. Le prime 19 di queste funzioni sono state tabulate da Curle(1962) ed esse sono sufficienti per includere tutti i termini fino a quello di ordine undicesimo nella (64). Nel paragrafo successivo verrà descritto il risultato dell'applicazione di questo metodo al flusso attorno a un cilindro circolare.

Anche il caso asimmetrico è stato preso in considerazione da Howarth, che ha calcolato le funzioni universali necessarie per i termini in x² ed x⁴; le tabelle di queste funzioni da lui computate si trovano in S. Goldstein (v., 1965²).

c) Strato limite laminare nel flusso attorno a un cilindro circolare, trascurando l'effetto di distacco sul flusso esterno.

Per un flusso ideale, irrotazionale e incompressibile, attorno a un cilindro circolare, con un flusso uniforme avente velocità U_∞ all'infinito, la teoria (v. sopra, cap. 2, È h) dice che la velocità della corrente libera sulla superficie del cilindro è data da

dove x è la distanza computata lungo la superficie del cilindro dal punto di ristagno anteriore, R è il raggio, così che x/R è l'angolo, misurato in radianti, tra il punto di ristagno anteriore e il punto x. Lo sviluppo in serie di Taylor di questa funzione U(x) ha la forma della (64), se si sostituisce R a l.

Il calcolo dello strato limite in questo caso, con il metodo descritto alla fine del paragrafo precedente, comprendente termini fino a x⁹, è riportato da Schlichting (v., 1960⁶). Fino a circa metà strada in direzione del punto di ristagno posteriore (cioè per x/R≤~π/2), l'andamento della velocità nello strato limite ha le stesse caratteristiche già viste nel caso della lamina piana (v. fig. 6); al di là di tale punto esso cambia come è mostrato schematicamente nella fig. 7. Oltre il punto di separazione indicato, che si trova a circa 110° dal punto di ristagno anteriore, stando alla teoria, si ha un riflusso in prossimità del cilindro. Le linee di corrente sono indicate schematicamente nella fig. 8 (in cui si è esageratamente ingrandito lo spessore dello strato limite).

La spiegazione fisica del riflusso può esser data nel modo che segue. Secondo l'equazione (67) e la legge di Bernoulli, la pressione p(x) diminuisce dal valore che ha nel punto di ristagno, in x/R=0, fino a un minimo per x/R=π/2, per poi ricrescere fino al valore di ristagno per x/R=π. Dopo essere stato accelerato dal gradiente di pressione, il fluido nel flusso libero ha una quantità di moto sufficiente per raggiungere, superando l'aumento di pressione, esattamente il punto di ristagno posteriore. Il fluido nello strato limite è soggetto agli stessi gradienti di pressione, entro l'approssimazione della teoria, ma viene anche rallentato dall'attrito e quindi si ferma prima.

d) Distacco dello strato limite.

Sperimentalmente il flusso che si osserva attorno a un cilindro circolare è completamente diverso da quello fornito dai risultati del calcolo precedente. Se il numero di Reynolds è sufficientemente basso perché i vortici al seguito non si spargano formando la cosiddetta scia vorticosa di Kármán (v. sotto), il flusso è del tipo di quello rappresentato schematicamente in fig. 9. Il punto di separazione si trova a circa 82° dal punto di ristagno anteriore, invece che a 110°, e la linea di corrente di separazione non giace presso la superficie del cilindro, ma se ne allontana lentamente e raggiunge il piano di simmetria in un punto di ristagno situato notevolmente a valle. Nella regione tra la linea di corrente di separazione e il cilindro ci sono due vortici disposti simmetricamente rispetto al piano di simmetria, a volte accompagnati da altri vortici molto più piccoli.

La spiegazione di questa discrepanza si trova fotografando il flusso prodotto da un cilindro che venga portato dalla sua condizione di quiete all'interno di un fluido alla velocità finale quasi istantaneamente. Si nota che, per un tempo brevissimo, prima che il cilindro si sia spostato di un tratto pari a una piccola frazione del suo diametro, il flusso è in buon accordo con i calcoli descritti precedentemente e con la figura, ma che, col procedere del tempo, la regione del riflusso cresce fino ad assumere approssimativamente le dimensioni indicate in fig. 9. Questa condizione si raggiunge solo dopo che il cilindro si è spostato di un tratto eguale ad alcuni diametri. Dato che il flusso non ammette un potenziale nella regione dei vortici, esso non è ivi calcolabile (a parte che per una forma di calcolo dipendente dal tempo, che parta dalle condizioni di quiete e usi le equazioni di Navier-Stokes, la quale sarebbe peraltro al limite delle possibilità dei calcolatori odierni). Per determinare la posizione del punto di separazione e lo strato limite fino a quel punto bisognerebbe calcolare le grandezze U(x) e p(x) del flusso libero a partire non dal flusso potenziale attorno a un cilindro circolare, ma dal flusso potenziale attorno al cilindro non circolare che include anche la regione racchiusa dalla linea di corrente di separazione. Poiché questa regione non è conosciuta teoricamente, vari ricercatori, a partire da K. Hiemenz (v., 1911), hanno usato valori sperimentali di U(x) o p(x), con l'uso dei quali le equazioni dello strato limite danno un punto di separazione situato a circa 82°, in buon accordo con quanto si osserva.

Per numeri di Reynolds al di sopra di circa 50-60 la situazione rappresentata in fig. 9 è instabile. Uno dei vortici, per esempio quello superiore, cresce a spese di quello inferiore, poi si stacca e discende la corrente, lasciando un piccolo vortice al suo posto. Poi cresce e si separa il vortice inferiore, e così via. L'alternato distaccarsi di vortici dalle due parti del cilindro dà luogo alla ben nota scia vorticosa di Kármán, che trasporta a valle energia cinetica e aumenta così la resistenza al moto del cilindro. Per numeri di Reynolds dell'ordine di qualche migliaio, la scia diviene completamente turbolenta. Il distacco dello strato limite ha luogo anche nel flusso attorno a un'ala, se l'angolo d'attacco diventa troppo grande; si sviluppa una regione di vortici e turbolenze immediatamente al di sopra e dietro l'ala, la portanza scende bruscamente a zero e aumenta la resistenza. Questo fenomeno è noto con il nome di ‛stallo'.

e) Teoria matematica delle equazioni dello strato limite.

I problemi matematici degli strati limite sono dipendenti dal tempo ab initio, come quasi tutti i problemi della fisica. La formazione di uno strato limite è cioè un problema a valori iniziali. Tutto quanto riguarda lo stato stazionario (esistenza, stabilità, ...) riguarda in realtà il comportamento asintotico, per t→∞, della soluzione del problema a valori iniziali. I punti principali riguardanti il problema a valori iniziali sono l'esistenza e l'unicità della soluzione e la sua dipendenza continua dai valori iniziali (se il problema è ben posto, nel senso di Hadamard) e, come si è detto sopra, il comportamento asintotico della soluzione. Questi problemi sono stati studiati ampiamente da O. A. Olejnik (v., 1969). Qui descriveremo solo alcuni risultati relativi al problema dello stato stazionario.

Per prima cosa, va spesa una parola sulla possibilità di controllare il distacco dello strato limite aspirando o soffiando attraverso piccoli fori o fessure della superficie dell'ala o di un altro oggetto su cui si formi lo strato. Nel paragrafo precedente, a proposito dello strato limite formantesi attorno a un cilindro perpendicolare al flusso, si è messo in evidenza che il distacco avviene perché il flusso nello strato limite, rispetto al fluido del flusso libero, è decelerato dall'attrito. Se si elimina il fluido decelerato aspirandolo all'interno del cilindro attraverso piccole aperture nella superficie, si può far arretrare la separazione in un punto posto più a valle e la si può eliminare completamente se c'è abbastanza aspirazione. Sistemi basati su quest'idea sono stati usati per fare ali che non siano soggette al fenomeno di stallo ad angoli di attacco più grandi di quelli altrimenti possibili (v. Schlichting, 1960⁶, cap. XIII).

La formulazione matematica è ancora basata sulle equazioni (57-60), in cui x e y sono coordinate curvilinee (cartesiane nel caso particolare della lamina piana), la parete è posta in y=0, le linee x=cost sono perpendicolari alla parete, U(x) e p(x) sono la velocità e la pressione nel flusso libero esterno. Tuttavia: 1) le condizioni al contorno (59) vanno generalizzate in

u(x, 0)=0, v(x, 0)=v₀(x), (68)

dove v₀(x) è negativa se si aspira attraverso la parete e positiva se si soffia; 2) è necessaria una condizione al contorno anche sulla linea x=0 perpendicolare alla parete nel punto in cui comincia lo strato limite. Questa condizione al contorno può essere di due tipi, secondo quanto segue. Nel caso di flusso sopra una lamina piana, in cui u(0, y)=U(∞) o, più generale, per il problema del prolungamento, in cui si suppone di conoscere u(0, y) su di un piano x=0 e si desidera calcolare lo strato limite a valle di questo piano, si ha la condizione:

u(0, y)=u₀(y), con u₀(y) assegnato. (69)

Invece, nel caso di un flusso simmetrico attorno a una forma simmetrica arrotondata sul fronte d'attacco, si ha:

U(0)=0 u(0, y)=0. (70)

Inoltre in questo caso U(x) e u(x, y) sono funzioni dispari di x, mentre p(x) è pari.

La condizione (69) non è apparsa esplicitamente nel cap. 5, È a, nella discussione dello strato limite al di sopra di una lamina piana; tuttavia, la soluzione (62-63) ha la proprietà che u, data da ∂ψ/∂y, tende a U(∞)f′(∞)=U(∞), per ogni y, quando x tende a 0; e quindi la (69) è soddisfatta con u₀(y)≡U(∞). La condizione (70) per il caso simmetrico è stata usata nel cap. 5, ÈÈ b e c, perché U(x) e ψ(x, y) sono funzioni dispari di x che si annullano per x=0.

Infine, c'è l'ovvia condizione asintotica che u(x, y)→U(x) per y→∞.

Uno dei risultati di Olejnik per il problema del flusso simmetrico afferma che, se U(x) è una funzione dispari e v₀(x) una funzione pari, ambedue sufficientemente regolari, il problema ha un'unica soluzione u(x, y) e v(x, y), per x contenuto all'interno di un certo intervallo [0, X]; in questa soluzione u e ∂u/∂x sono positive, per y>0, e u(x, y) tende esponenzialmente (e uniformemente rispetto a x) a U(x), per y tendente all'infinito. Inoltre, il teorema di Olejnik elenca varie disuguaglianze soddisfatte da u e dalle sue derivate parziali.

Per il problema del prolungamento vale un risultato analogo.

Il risultato precedente riguarda la soluzione locale, nel senso che l'esistenza viene dimostrata solo per un certo intervallo [0, X] (che potrebbe anche essere molto piccolo). Olejnik ha anche ottenuto risultati globali; li enunceremo per il problema del prolungamento, in cui u è nota su di un piano iniziale x=0:u(0, y)=u₀(y). In primo luogo, u₀(y) deve soddisfare alcune condizioni fisicamente ragionevoli, cioè u₀(0)=0, u₀(y)>0 per y>0, u0′ (0)>0, u₀(y)→U(0)>0, per y→∞. Inoltre, per x=0 e y=0, il primo termine a primo membro della (57) è nullo: c'è quindi una condizione di compatibilità tra u₀(y) e v₀(x), data da

La pressione p(x) nel flusso libero dipende dalla U(x) assegnata secondo la legge di Bernoulli: ρ+½ρU²=cost. Nei casi che interessano, p(x) inizialmente diminuisce e poi aumenta, al crescere di x, come nel problema del flusso attorno a un cilindro o a un'ala col bordo d'entrata arrotondato.

Un primo risultato generale è dato dal fatto che se p′(x)〈0, per ogni x in un intervallo [0, A], o se p′(x)≤0 e v₀(x)≤0 (cioè si può aspirare, ma non soffiare, a meno che la pressione non stia effettivamente diminuendo), per ogni x nell'intervallo, allora per ogni x in [0, A] esiste un'unica soluzione.

Nel caso del flusso attorno a un cilindro circolare, se si trascura l'effetto del distacco dello strato limite sul flusso esterno, questo risultato di Olejnik assicura l'esistenza e l'unicità della soluzione (cioè senza separazione) fino al punto che si trova a 90° dal punto di ristagno anteriore.

Il successivo risultato di Olejnik ci assicura che la separazione può essere completamente evitata mediante opportuna aspirazione: se, per ogni x in [0, A], è v₀(x)≤0 ogniqualvolta p′(x)=0 e inoltre v₀(x) è negativo e sufficientemente grande ogniqualvolta è p′(x)>0, allora esiste un'unica soluzione nell'intero intervallo [0, A]. (Questo risultato non implica un aumento senza limite della pressione p(x) al crescere di x, perché p(x) è sempre limitato dal valore che assume nel punto di ristagno, per la legge di Bernoulli).

L'ultimo risultato di Olejnik che citeremo qui è il reciproco del precedente: soffiando opportunamente (v₀(x) sufficientemente grande e positivo) la separazione può essere prodotta in un punto arbitrariamente vicino (nel senso delle x crescenti) dopo che la ptessione abbia raggiunto un minimo e poi rispetti la condizione p′(x)≥0.

f) Lo strato limite turbolento.

In mancanza di un'autentica teoria della turbolenza, la nostra conoscenza degli strati limite turbolenti è essenzialmente empirica, guidata da qualche principio teorico. La nostra discussione sarà limitata allo strato limite sopra una lamina piana; in questo caso, come già detto, il numero di Reynolds locale per lo strato limite laminare, R=U_∞δ/ν, cresce come √-x da valori piccoli, vicino al bordo della lamina, a valori infinitamente grandi per x→∞. Nel prossimo capitolo vedremo che il flusso diventa instabile per R≃420, quando si sviluppano piccole oscillazioni che si amplificano gradualmente a mano a mano che ci si muove nel verso della corrente. Se R cresce ulteriormente anche altri modi diventano instabili e lo strato limite diventa completamente turbolento per numeri di Reynolds compresi tra 3•10³ e 3•10⁶, a seconda della quantità di turbolenza residua nel fluido circostante e della regolarità della superficie della lamina. Qui considereremo soltanto il caso di turbolenza pienamente sviluppata.

Le componenti della velocità u, v e w saranno scritte nel modo: ū+u′, ecc., in cui la soprassegnatura indica che si è eseguita la media rispetto al tempo della grandezza. Ricordiamo dal cap. 4 che il tensore di Reynolds, dato dalla (30), influenza il flusso medio nel modo indicato dalla (29) (la differenza tra le notazioni del cap. 4 e quelle usate qui è ovvia). Nel problema che stiamo trattando il flusso medio è stazionario (indipendente dal tempo), perché è stazionario il flusso esterno, quindi tutte le forze, mediate, sono in equilibrio. Come nel caso laminare, supponiamo che lo spessore δ dello strato limite sia piccolo rispetto alle distanze entro cui δ e le altre grandezze caratteristiche del flusso cambiano in modo apprezzabile lungo la lamina. È quindi ancora valida l'approssimazione che il flusso sia quasi piano e parallelo. Essendo la pressione p costante nel flusso esterno ed essendo la sua variazione attraverso lo strato limite una quantità piccola, del secondo ordine, p può essere considerata costante. Quindi τ_xy, l'unica componente non nulla dello sforzo totale; data da

ha un valore costante τ₀, che è uguale alla resistenza d'attrito (o ‛attrito di superficie') per unità d'area della lamina.

La descrizione generale del flusso è la seguente. Essendo u′=v′=0 sulla superficie della lamina (in y=0), l'intera tensione τ₀ deve essere prodotta, sulla superficie, dal termine di viscosità μ(∂ū/∂y). In uno strato molto sottile vicino alla lamina, detto ‛strato viscoso' (talvolta, imprecisamente, ‛strato laminare'), il grado di turbolenza è abbastanza basso perché lo sforzo di Reynolds −ρ-u-′-v-′ sia trascurabile rispetto a τ₀. Inoltre, in uno strato adiacente di transizione (anch'esso molto sottile) i due termini della (72) sono paragonabili. Per la maggior parte dello spessore dello strato limite, lo sforzo τ₀ è dovuto quasi esclusivamente al termine di Reynolds. Sulla superficie esterna dello strato limite (in y≃δ) la turbolenza decresce abbastanza bruscamente. (Secondo Schlichting, per 0,6 δ〈y〈1,2 δ, la turbolenza generalmente è pulsante o intermittente; solitamente si fa l'ipotesi che queste pulsazioni non abbiano effetto sul flusso medio).

Il meccanismo mediante il quale il flusso esterno esercita lo sforzo τ₀ sullo strato limite è l'intrappolamento. Lo spessore δ aumenta, anche se lentamente, al crescere di x. Quindi nuovo fluido, che inizialmente si muoveva a velocità U_∞, viene gradualmente incorporato nello strato limite, che è più lento. La diminuzione di quantità di moto subita da questo fluido per unità di tempo produce sul fluido contenuto entro lo strato limite la forza τ₀ nella direzione x, per unità d'area della lamina. In effetti, è proprio questo meccanismo che determina la tensione τ₀ che vien trasmessa alla lamina attraverso lo strato limite.

Possiamo ottenere informazioni sull'andamento generale della funzione ū(y), che descrive l'andamento della velocità attraverso lo strato limite, da principi di similitudine. Nell'approssimazione in cui δ si considera localmente costante, il problema è caratterizzato dai parametri τ₀, ρ, e ν, la cui unica combinazione adimensionale con la variabile indipendente y,

ha la struttura di un numero di Reynolds, avendo √-τ-₀-/-ρ le dimensioni di una velocità. Pertanto, l'andamento generale del flusso dovrebbe essere lo stesso per tutti gli strati limite turbolenti aventi lo stesso valore di η, a condizione di usare opportune unità per la misura delle lunghezze, delle velocità, ecc. In particolare, come unità di misura per ū va preso √-τ-/-ρ ; quindi

dove f è una funzione universale valida per tutti gli strati limite piani e completamente turbolenti, a condizione che la compressibilità, il trasporto del calore, le asperità delle pareti, ecc., possano essere trascurate.

La (74), che è stata ottenuta da Prandtl, è stata chiamata ‛legge della parete' da Monin e Yaglom e nel loro lavoro se ne trova un'ampia verifica sperimentale in forma grafica.

La teoria generale dà qualche informazione sulla forma generale di f in due casi limite: per η molto piccolo (〈~5) e per η molto grande (>~30).

In primo luogo, essendo u′, v′ e w′ nulle sulla superficie della lamina (in y=0) insieme con le loro derivate rispetto a x e z (z è la coordinata cartesiana giacente sulla lamina e perpendicolare al flusso e w′ è la corrispondente componente della velocità) e dato che, per l'equazione di continuità, ∇•v′=0, è nulla anche ∂v′/∂y in y=0, se si differenzia la (72) si vede che la seconda e terza derivata di ū rispetto a y sono nulle per y=0, quindi f″(0)=f‴(0)=0. Inoltre, è ū(0)=0 e ∂ū(0)/∂y=τ₀/μ=τ₀ρ/ν e quindi f(0)=0 e f′(0)=1. Ci si aspetta pertanto che nello strato viscoso sia valida l'approssimazione f(η)≃η: per η〈~5, essa è in accordo con l'esperienza entro qualche unità per cento.

In tutta la regione al di sopra dei sottili strati viscoso e di transizione, cioè per ogni valore sufficientemente grande di η, l'andamento generale del flusso, in base alla (74), dovrebbe essere indipendente da ν, per valori dati di ρ₀ e τ₀. Questo significa semplicemente che ∂ū/∂y, non ū, deve essere indipendente da ν, dato che l'aggiunta a ū di un termine costante non cambia l'andamento generale del flusso. (La velocità costante da aggiungere è in effetti il differenziale della velocità attraverso lo strato viscoso, che è proporzionale a 1/ν). Dalla (74) si ottiene

in cui la costante non dipende da ν. Pertanto è f′(η)=cost/η ed f(η) ha la forma seguente:

f(η)=A ln η+B, per η>η₀. (75)

I migliori valori sperimentali per A, B ed η₀ secondo Monin e Yaglom, sono: A=2,5, B=5,1 e η₀~30. Con questi valori la (75) si accorda con l'esperienza entro qualche per cento, per ~30〈η〈10³.

La (75) è detta ‛legge dello strato limite logaritmico': essa è valida, naturalmente, solo fino a un certo valore di η che corrisponde alla sommità dello strato limite, cioè fino a η=(δ/ν)√-τ-₀-/-ρ. Ragionamenti qualitativi suggeriscono che δ vari più o meno proporzionalmente a x. Il coefficiente d'attrito

non è fornito dalla teoria e deve essere ottenuto sperimentalmente.

Uno strato limite turbolento ha minor tendenza al distacco di uno strato laminare. Si osserva che il punto di distacco su una sfera o su un cilindro si sposta bruscamente all'indietro quando il numero di Reynolds supera il valore di circa 3 o 4•10⁵; contemporaneamente, la resistenza diminuisce di un fattore 4 o 5, mentre diminuisce l'ampiezza della scia. Si può ottenere lo stesso effetto, a numeri di Reynolds più bassi, inducendo artificialmente la turbolenza mediante piccole sporgenze sulla superficie. (A questo scopo piccole sporgenze a forma di pinna sono a volte messe sulla superficie superiore delle ali per prevenire lo stallo). Se lo strato limite diventa turbolento prima di raggiungere il punto di distacco, il riflusso rappresentato nelle figg. 7 e 8 non si può sviluppare così facilmente, perché il fluido di quella regione si mescola costantemente col fluido di strati leggermente più esterni, che hanno una maggiore quantità di moto in avanti.

6. Instabilità dei flussi stazionari; insorgere della turbolenza.

Il problema della stabilità dinamica del fluido rispetto a piccole perturbazioni è il seguente: siano U(x) e P(x) i campi di velocità e di pressione di una soluzione stazionaria delle equazioni di Navier-Stokes con opportune condizioni al contorno. Consideriamo la soluzione generale, con i campi di velocità e di pressione dati da U(x)+u′(x, t) e P(x)+p′(x, t). Supponendo che il problema a valori iniziali sia ben posto, desideriamo stabilire se u′(x, t) e p′(x, t) tendono a 0 in qualche modo (per esempio uniformemente rispetto alla x), per t→∞, per ogni perturbazione iniziale u′(x, 0), p′(x, 0) che sia in qualche modo sufficientemente piccola (per esempio, di nuovo, uniformemente rispetto alla x). Solo di recente è stato possibile affrontare con metodi matematici il problema così formulato e il lettore è rimandato al libro di Monin e Yaglom (v., 1971) o all'articolo di Kirchgässner e Kielhöfer (v., 1973) per una panoramica su un aspetto del problema.

Il procedimento che è stato normalmente seguito, a partire dal lavoro di Taylor nel 1923, è di linearizzare le equazioni in u e p. La giustificazione è basata in parte sul generale successo che hanno le linearizzazioni di questo tipo in altri problemi analoghi della fisica matematica e in parte sull'ottimo accordo tra i risultati calcolati mediante la linearizzazione e l'esperienza, specialmente nel problema del flusso di Couette tra cilindri rotanti. L'idea che sta dietro alla linearizzazione è di scrivere u e p nella forma:

dove ε è un parametro, da considerarsi piccolo; le equazioni per le funzioni u_k e p_k si ottengono quindi sostituendo queste serie nelle equazioni (19) e (20) di Navier-Stokes e nelle condizioni al contorno, supponendo che le serie convergano e che siano differenziabili termine a termine. Si suppone poi che i primi termini εu₁ ed εp₁ siano delle approssimazioni adeguate per u′ e p′; per essi si ottengono allora le equazioni lineari seguenti:

dove U=U(x) è il campo di velocità imperturbato e ν=μ/ρ è il coefficiente di viscosità cinematica. Dato che nei coefficienti non appare il tempo t, le equazioni linearizzate hanno soluzioni con modi normali, cioè soluzioni del tipo e^σt moltiplicato per una funzione di x. Generalmente si fa l'ipotesi che i modi normali formino una base completa di funzioni per lo sviluppo di una perturbazione iniziale arbitraria, così il flusso imperturbato è stabile se e solo se Re(σ)〈0 per ogni modo normale (si confronti tuttavia il cap. 6, È f, per un metodo più rigoroso, che spesso può essere usato).

Spesso si trova che il flusso è stabile, in base al criterio precedente, per ogni valore sufficientemente piccolo del numero di Reynolds R del flusso imperturbato. Al crescere di R, normalmente Re(σ) cresce fino a che, per un certo valore critico R_cr di R, esso diventa zero per uno dei modi normali; R_cr è allora il numero di Reynolds limite per la stabilità del flusso stazionario.

a) I principali problemi standard.

1. Il flusso si dice di ‛Poiseuille' quando avviene in una condotta o in un canale tra due pareti fisse (v. fig. 10). La condizione al contorno è che la velocità del fluido si annulli sulle pareti ovvero che non vi sia scorrimento. Nel flusso stazionario o ‛laminare', la velocità è diretta secondo z o x, rispettivamente, ed è una funzione quadratica della coordinata trasversale (r o y), le costanti che intervengono in questa funzione quadratica essendo tali da soddisfare la condizione di assenza di scorrimento; un gradiente uniforme di pressione lungo la condotta o il canale è necessario per mantenere il flusso. Il problema consiste nella determinazione delle condizioni di stabilità del flusso laminare.

2. Il flusso di ‛Couette' è originato dal moto di una parete parallela al flusso. Nella fig. 11A una delle due pareti piane e parallele si sta spostando rispetto all'altra; in condizioni di stato stazionario, la velocità del fluido è una funzione lineare della coordinata trasversale. Nella fig. 11B il flusso ha luogo tra due cilindri coassiali rotanti, che possono essere in rotazione nello stesso senso o in senso opposto; in condizioni di flusso stazionario la velocità del fluido, che è nella direzione ϑ delle coordinate cilindriche r, ϑ, z, ha modulo Ar+B/r, in cui A e B sono tali per cui non vi è scorrimento. Il problema è ancora quello di determinare le condizioni di stabilità del flusso laminare.

3. Un altro problema importante è quello di determinare la stabilità di uno strato limite, come nel caso per esempio della soluzione di Blasius per lo strato limite su di una lamina piana, che è stato descritto nel cap. 5.

Questi problemi sono d'interesse per le applicazioni pratiche e anche come prova dello sviluppo della conoscenza dei principi fisici implicati. Faremo in ciò che segue alcune considerazioni qualitative su questi problemi.

b) Flusso di Poiseuille in una condotta a sezione circolare.

Per il principio di similitudine di Reynolds, il flusso di Poiseuille dovrebbe essere completamente determinato dal numero di Reynolds R=DV/ν, dove D è il diametro, V la velocità mediata sulla sezione (in modo che il flusso di volume sia πVD²/4) e ν il coefficiente di viscosità cinematica. In particolare, ci si potrebbe aspettare che il flusso laminare sia stabile per R minore di un certo valore R_cr e instabile per R maggiore di R_cr, ma sperimentalmente non è stato trovato nessun numero di Reynolds limite R_cr. Invece, il valore di R a cui comincia la turbolenza varia da circa 2.000 a circa 100.000 e sembra dipendere esclusivamente dalla presenza iniziale di perturbazioni di ampiezza finita, anche se forse molto piccola, e causate da asperità o irregolarità delle pareti della condotta, turbolenza residua nel serbatoio da cui viene il liquido e turbolenza incipiente causata da spigoli, anche se arrotondati, all'attacco della condotta al serbatoio. Intervengono evidenti effetti di non linearità: una perturbazione di ampiezza finita può essere instabile in condizioni in cui una perturbazione simile di ampiezza minore o infinitesima sarebbe stabile. A un estremo, se non si prende nessuna precauzione per ridurre le perturbazioni iniziali, il limite sembra essere attorno a 2.000. Per R〈2.000, anche una turbolenza pienamente sviluppata viene smorzata, con l'avanzare del fluido nella condotta. All'altro estremo, un flusso è stato mantenuto laminare fino a valori di R=100.000, prendendo grandissime precauzioni, e non sembrano esservi ragioni per dubitare che si possano raggiungere valori di R ancora più alti, in linea di principio.

La teoria della stabilità linearizzata, basata sulle precedenti equazioni (77), sembra essere in accordo con questa esperienza. Adesso si crede che, nel caso particolare del flusso di Poiseuille in una condotta circolare, il flusso laminare sia stabile rispetto a una qualunque perturbazione infinitesima, per ogni numero di Reynolds. Tuttavia, un'analisi matematica è difficile perché le funzioni dei modi normali sono complicate; solo recentemente essa è stata sviluppata fino a tal punto da non lasciare più dubbi ragionevoli sulla stabilità, e non è ancora stato dimostrato che i modi normali studiati finora costituiscano una base completa di funzioni. In questo caso, il valore di R_cr previsto dal principio di similitudine di Reynolds sembra essere ∞.

Un'altra previsione del principio di similitudine, che è stata sufficientemente confermata, è che, una volta che in una condotta si sia stabilita una turbolenza pienamente sviluppata, il gradiente di pressione diviso per ½ρV²/D, cioè

che è detto coefficiente di attrito, dovrebbe dipendere dal solo numero di Reynolds R=VD/ν. Nel lavoro di Bakhmeteff (v., 1941) sono presentate alcune misure preliminari in un grafico di C in funzione di R, per flussi di aria e acqua in condotte di varie dimensioni; tutti i punti sperimentali si trovano sulla stessa curva, entro gli errori sperimentali, per R maggiore di circa 3.500. Una conseguenza importante di questo risultato, che non è sempre stata messa chiaramente in evidenza e che sopra è stata tacitamente supposta, è che, almeno in una condotta, ha senso parlare di turbolenza pienamente sviluppata; il regime pienamente turbolento dipende solo dal numero di Reynolds e non, per esempio, dalla storia precedente degli elementi di fluido molto più a monte nella condotta.

c) Flusso di Poiseuille piano.

La teoria generale della stabilità dei flussi piani e paralleli è descritta brevemente nel cap. 5, È f. Qui facciamo notare la differenza sorprendente tra il caso circolare e quello piano. Il flusso di Poiseuille piano diventa instabile a un numero di Reynolds R_cr≃5.772 con un modo normale consistente in grossi nuclei vorticosi: la correzione del primo ordine al flusso laminare è indicata schematicamente dalle linee di corrente della fig. 12 (il flusso è indipendente dalla coordinata perpendicolare al piano del disegno). L'intera struttura si sposta a valle con una velocità di poco inferiore a metà della velocità media V del flusso non perturbato. C'è una famiglia di modi normali di questo tipo, dipendente da un solo parametro k=2π/λ, dove λ è la lunghezza d'onda indicata nella figura. I modi normali di questo tipo sono instabili nella regione del piano k, R indicata nella fig. 13.

d) Flusso piano di Couette.

A differenza del flusso di Poiseuille, il flusso di Couette è apparentemente stabile nel caso piano. Tuttavia, va notato che i casi cilindrici non sono assolutamente paragonabili; nel flusso di Poiseuille in una condotta circolare la velocità del fluido non perturbato è nella direzione z, mentre nel caso del flusso tra due cilindri rotanti è nella direzione ϑ (con r, ϑ e z coordinate cilindriche). Il caso di flusso tra due cilindri coassiali, con la velocità relativa nella direzione z, non sembra che sia mai stato studiato, presumibilmente per l'impossibilità della verifica sperimentale.

Come nel caso del flusso di Poiseuille in una condotta circolare, la teoria della stabilità è stata affrontata con grandi difficoltà matematiche. Vari tentativi di sistemare la questione, dal 1906 ai nostri giorni, non sono approdati a importanti conclusioni, ma adesso sembra quasi certo, secondo Monin e Yaglom, che il flusso piano di Couette sia stabile a tutti i numeri di Reynolds.

e) Flusso di Couette tra cilindri rotanti.

L'analisi di G. I. Taylor del 1923 sulla stabilità del flusso tra cilindri coassiali rotanti è stato il maggior trionfo della teoria della stabilità in questo campo e forse anche dei metodi sperimentali, perché Taylor ha presentato sia i risultati teorici sia le verifiche sperimentali, che hanno trovato ampia conferma anche in seguito. Ulteriore lavoro è stato dedicato al miglioramento e alla semplificazione dei metodi di calcolo e all'esame di un'ipotesi fatta da Taylor, che si è rivelata corretta nella maggior parte dei casi, ma non in tutti.

Siano r₁ ed r₂ i raggi delle superfici cilindriche, interna ed esterna rispettivamente, che confinano il fluido e siano Ω₁ e Ω₂ le loro velocità angolari. Per un valore r del raggio (r₁≤r≤r₂) il flusso non perturbato ha la velocità angolare

Ω(r)=A+B/r², (78)

dove A e B sono determinate dalle condizioni di non scorrimento: Ω₁=A+B/r²₁ e Ω₂=A+B/r²₂. Il problema è caratterizzato da vari parametri adimensionali, come r₁/r₂ e Ω₁/Ω₂ (quest'ultimo potendo essere ovviamente anche infinito). Conviene immaginare fisso il rapporto r₁/r₂ e rappresentare il flusso non perturbato mediante i parametri

aventi la struttura di numeri di Reynolds (naturalmente possono essere positivi, negativi o nulli); un semplice ragionamento proposto in precedenza da Rayleigh assicura che il flusso è stabile se questi parametri hanno lo stesso segno e se il primo è in modulo minore del secondo (cioè se 0≤Ω₁r²₁/Ω₂r²₂〈1).

Se nelle equazioni (77) si passa alle coordinate cilindriche r, ϑ e z (non è necessario scrivere esplicitamente le equazioni risultanti, che sono abbastanza lunghe), i coefficienti non solo non dipendono da t, ma neanche da ϑ e z, dato che il flusso non perturbato (78) dipende solo da r. Ci sono pertanto dei modi normali in cui p′ e le componenti (cilindriche) di u′ sono del tipo

f(r)e^{i(kz+nϑ)+σt} (80)

con k reale arbitrario ed n intero. (Nella (80) f(r) denota una funzione diversa per p′ e per ogni componente di u′, ma l'esponenziale è sempre lo stesso). Se si introducono queste espressioni nelle equazioni a derivate parziali, ne risulta un sistema di equazioni differenziali ordinarie del quarto ordine per le funzioni di r, simile al sistema dato nel paragrafo seguente. Questo sistema, insieme con le condizioni al contorno per r=r₁ ed r=r₂, costituisce un problema agli autovalori per σ, se sono dati k, n e i parametri (79). Il problema agli autovalori è abbastanza complicato, ma si possono usare vari sviluppi in serie e vari metodi numerici per la sua soluzione.

Taylor, su basi intuitive, ha fatto l'ipotesi che i primi modi a diventare instabili abbiano n=0 e consistano pertanto in anelli vorticosi circolari paralleli attorno al cilindro, piuttosto che in perturbazioni elicoidali. Gli auto- valori di σ sono allora funzioni solamente del numero d'onda k nella direzione z, per un dato flusso; σ raggiunge il valore massimo σ_max per un certo valore di k; per ogni valore di X₂=Ω₂r²₂/ν, σ_max è negativo se X₁=Ω₁r²₁/ν è sufficientemente piccolo, ma cresce al crescere di X₁ e passa attraverso lo zero per un certo valore critico di X₁, che può essere considerato come il valore limite del numero di Reynolds per la stabilità, per un dato X₂. Nella fig. 14 è rappresentato il valore limite di X₁ in funzione di X₂ nel caso studiato da Taylor, in cui r₂/r₁ valeva 1,136. I valori misurati da Taylor erano in accordo con i valori della curva entro l'errore sperimentale (1-2%), per X₂ compreso nell'intervallo tra −650 e +2.200.

Calcoli più recenti di Krueger, Gross e Di Prima e il lavoro sperimentale di vari ricercatori (v. Monin e Yaglom, 1971) hanno dimostrato che, per valori sufficientemente negativi di Ω₂r²₂/ν, (si è scelto Ω₁ positivo, quindi Ω₂ negativo significa che i cilindri stanno ruotando in senso opposto), il primo modo a diventare instabile non si ha per n=0, ma per n=1, 2, 3 ..., con n che cresce a mano a mano che Ω₂r²₂/ν diventa più negativo. Questi modi consistono di vortici elicoidali. La curva di Taylor va quindi modificata leggermente, alla sinistra della fig. 14, in una zona non coperta dalle misure di Taylor. La modifica è molto piccola e in effetti i valori di σ_max per n diversi da zero, ma piccoli, differiscono solo leggermente dai valori per n=0 in tutta la zona del grafico.

Quando domina il modo n=0, l'autovalore σ è reale. Quindi il flusso perturbato che sostituisce il flusso originale, quando è stato superato (ma solo di poco) il limite di stabilità, non è un flusso pulsante o turbolento, ma un altro flusso stazionario, il cosiddetto ‛flusso secondario', i cui anelli vorticosi sono stazionari. Questo fenomeno, che si verifica spesso, è detto principio di ‛scambio delle stabilità' (un flusso stabile e stazionario è sostituito da un altro); tuttavia, non esiste una base generale per questo principio.

La sostituzione del flusso primario con quello secondario, quando si raggiunge il numero critico di Reynolds, si accompagna a un fenomeno di biforcazione. In corrispondenza ad un numero di Reynolds un po' più alto, si ha una seconda biforcazione, in cui i vortici circolari di Taylor sono sostituiti da vortici ondosi, come fu osservato nel 1923 da Taylor e confermato in seguito da altri ricercatori. Recentemente i vortici di Taylor e quelli ondosi sono stati studiati sperimentalmente da Coles, Snyder e altri e teoricamente da Eckhaus, Kogelman, Davey, Di Prima, Stuart e altri. Vi sono indizi di una terza biforcazione, a un numero di Reynolds ancora più alto, che porta vortici pulsanti. Ad ogni nuova biforcazione il flusso diventa un po' più complesso; Landau e Hopf, nel 1940, avanzarono l'ipotesi che l'instaurarsi della turbolenza avvenga in questo modo. Tuttavia, in un recente. lavoro basato sulla moderna teoria dei sistemi dinamici, Ruelle e Takens (v., 1971) suggeriscono l'ipotesi che la turbolenza possa invece instaurarsi improvvisamente dopo tre o quattro biforcazioni.

È anche stato studiato l'effetto di un campo magnetico su questo tipo di flusso, quando il fluido è conduttore (v. Chandrasekhar, 1961; v. Lin, 1955).

f) Strato limite su una lamina piana; teoria generale della stabilità dei flussi piani e paralleli, viscosi e non viscosi.

È stato notato (v. sopra, È a) che in un flusso stazionario piano e parallelo di un fluido viscoso la velocità è sempre una funzione quadratica della coordinata perpendicolare ai piani del flusso. Per un flusso tra pareti parallele, quindi, il caso generale è una combinazione del flusso piano di Poiseuille col flusso piano di Couette. Anche lo strato limite sopra una lamina piana è, con ottima approssimazione, un flusso piano e parallelo, secondo la teoria di Blasius, dato che l'aumento dello spessore dello strato limite con la distanza dal margine della lamina è molto graduale e che la componente verticale della velocità è una quantità piccola del primo ordine, rispetto alla componente parallela. La maggior parte degli studi sulla stabilità dello strato limite è stata basata sull'approssimazione di flusso piano e parallelo. La validità di questa approssimazione per il flusso nello strato limite, in vista della natura abbastanza complicata del problema della stabilità in altri casi (specialmente per il flusso piano di Couette e quello in condotta circolare di Poiseuille), è stata oggetto di molti studi (v. Betchov e Criminale jr., 1967), che finora però non hanno dato grandi risultati.

Per il flusso piano e parallelo, siano x, y e z le coordinate cartesiane tali che il flusso non perturbato avvenga nella direzione x con velocità U(y). Supponiamo che il flusso occupi la regione 0≤y≤y₀, o 0≤y〈∞, e che ci sia una condizione di non scorrimento U(0)=0, u′(0)=0 (per tutte le componenti). I coefficienti delle equazioni a derivate parziali (77) dipendono allora solo da y; esistono, quindi, dei modi normali in cui p′ e tutte le componenti di u′ sono del tipo

f(y)e^{i(kxx+kzz)+ σt}. (81)

H. B. Squire ha dimostrato (v., 1933) che questo modo diventa instabile a numeri di Reynolds più grandi rispetto al corrispondente modo in cui k_x è sostituito da (k²_x+k²_z)^1/2 e k_z da zero. È quindi sufficiente considerare il problema bidimensionale seguente:

La corrente ψ, definita dalle equazioni u′=−∂ψ/∂y e v′=∂ψ/∂x, soddisfa l'equazione

Per ottenere la soluzione del modo normale, ψ(x, y, t) viene scritta nella forma ϕ(y) exp[ik(x−ct)], dove σ è stato sostituito da −ick, in accordo con le notazioni più usuali: la stabilità richiede che sia Im(c)≥0. Sostituendo nella (83) si ottiene per ϕ(y) la cosiddetta equazione di Orr-Sommerfeld:

dove gli apici indicano derivazione rispetto alla y. Con opportune condizioni al contorno la (84) è un problema agli autovalori per c. Su una parete rigida la condizione al contorno è ϕ=0, ϕ′=0. Se il flusso si estende all'infinito, allora ϕ(y) tende a 0 per y che tende a ∞.

Per lo strato limite su una lamina piana, U(y) è data dalla teoria di Blasius ed è rappresentata graficamente in fig. 6. Soluzioni del problema agli autovalori in questo caso sono state ottenute da molti ricercatori, tra cui principalmente Tollmien, Schlichting, Lin e Shen. Si è trovato che il numero di Reynolds limite per la stabilità è

dove δ* è lo spessore dello strato limite dalla lamina al piano in cui U(y) è pari al 99% del valore che assume nella corrente libera, cioè u(δ*)=0,99 u(∞). La regione di instabilità nel piano k, R è qualitativamente simile a quella per il flusso piano di Poiseuille indicata nella fig. 13.

Relazioni tra flusso viscoso e non viscoso. - Dato che le instabilità normalmente appaiono per grandi valori del numero di Reynolds, quindi per ν piccoli, è interessante il caso limite di ν che tende a 0, specialmente perché l'equazione del quarto ordine (83) di Orr-Sommerfeld si riduce all'equazione del secondo ordine di Rayleigh

(U−c)(ϕ″−k²ϕ)−U″ϕ=0. (86)

Per lungo tempo si è creduto che la viscosità avesse necessariamente un effetto stabilizzatore, così che la stabilità del flusso non viscoso (ma con la U(y) presa ancora dalla soluzione stazionaria del problema del flusso viscoso) doveva essere una garanzia per la stabilità del flusso viscoso; ma questa credenza si è rivelata falsa. In particolare, nel 1880 Rayleigh aveva dimostrato che il corretto problema agli autovalori associato all'equazione (86) non ha soluzioni per c non reale, a meno che nella regione del flusso non ci sia un y tale che U″(y)=0; quindi, concludeva Rayleigh, lo strato limite sopra una lamina piana e il flusso piano di Poiseuille, per entrambi i quali è U″(y)〈0 per ogni y, dovrebbero essere completamente stabili, contrariamente a quanto si è visto in precedenza. (Il ragionamento di Rayleigh era incompleto, ma la sua conclusione sulla stabilità dei flussi non viscosi era corretta, come spiegato più oltre). La soluzione di questo apparente paradosso sta nella forma della regione d'instabilità indicata nella fig. 6. Sulle curve che danno gli estremi superiore e inferiore della regione d'instabilità, k tende a 0 al tendere di R all'infinito, cioè al tendere a zero della viscosità. Quindi, per ogni lunghezza d'onda 2π/k fissata, la perturbazione è stabile per tutti i valori di R sufficientemente grandi, mentre per ogni R>R_cr, c'è sempre qualche valore di k per cui la perturbazione è instabile. In questo senso la viscosità è una causa d'instabilità.

L'equazione di Rayleigh (86) presenta altre difficoltà. Si può dimostrare che ogni autovalore reale c deve essere compreso tra il massimo e il minimo di U(y). Quindi la (86) ha sempre un punto singolare, precisamente per quel valore di y per il quale U(y)−c=0; e questo complica l'analisi. Inoltre, è stato dimostrato da Lin (v., 1955) che, a meno che non esista un valore di y per cui sia U″(y)=0, non solo non esistono autovalori c non reali (risultato di Rayleigh), ma non ne esistono neanche di reali, mentre l'analisi dei modi normali presuppone che, per ogni k, le autofunzioni ϕ(y) formino una base completa di funzioni. Evidentemente va preso in considerazione un qualche tipo di spettro continuo.

Queste difficoltà sono state superate indipendentemente da Case e da Dikii nel 1960 (v. Monin e Yaglom, 1971). Per studiare il caso incompressibile, essi riconsiderarono l'equazione a derivate parziali (83) con il secondo membro posto uguale a zero. Risolsero il problema a valori iniziali di questa equazione per una funzione iniziale arbitraria ψ(x, y, 0)=ψ₀(x, y), usando le trasformazioni di Laplace rispetto a t ed evitando così la necessità dello sviluppo nei modi normali. In questo modo, essi furono in grado di dimostrare che il flusso piano di Poiseuille e lo strato limite di Blasius sono stabili nel caso non viscoso; cioè che la soluzione ψ(x, y, t) del problema a valori iniziali tende sempre a zero per t→∞. Più in generale, hanno dimostrato che anche quando l'equazione di Rayleigh (86) ha autovalori la parte di ψ(x, y, t) associata allo spettro continuo tende a zero per t→∞. Infine, hanno dimostrato che l'equazione completa (83) per il caso viscoso può anch'essa essere trattata col metodo della trasformazione di Laplace.

7. Convezione termica.

Sebbene di norma in questo articolo non si discutano effetti termici, il problema della convezione è così importante per l'astrofisica e così strettamente collegato col problema della turbolenza che presenteremo qui una breve discussione riguardante: 1) le instabilità che portano all'instaurarsi della convezione; 2) l'impostazione astrofisica del problema della convezione.

a) Il problema di Bénard.

Attorno al 1900 H. Bénard studiò il moto di un fluido scaldato dal basso all'interno di un recipiente a fondo piatto, che si suppone esteso indefinitamente nelle direzioni orizzontali. A causa dell'espansione termica, il fluido riscaldato è sottoposto a forze ascensionali e tende a salire, causando così moti di mescolamento nel fluido. Se il calore viene ceduto a un tasso sufficientemente basso, lo stato stazionario del fluido è stabile, a causa dello smorzamento dei moti di mescolamento dovuto alla viscosità, mentre, per un certo valore critico della potenza termica somministrata, ha inizio un flusso secondario. Normalmente si trascura la compressibilità del fluido ma non la sua dilatazione termica, secondo l'approssimazione così detta di Boussinesq. (In problemi di struttura stellare non si può trascurare la compressibilità e si usa l'approssimazione anelastica, leggermente più complicata; v. Spiegel, 1971).

Sia d lo spessore dello strato, z la coordinata verticale misurata dal fondo del recipiente e supponiamo che attraverso lo strato si mantenga una differenza di temperatura costante ΔT, la superficie più calda essendo quella inferiore. Nello stato stazionario la velocità U è nulla, la temperatura varia linearmente con z e la pressione P è in equilibrio idrostatico: dP/dz=−ρg. Le deviazioni da questi valori sono indicate con u′, T′ e P′. Lo scostamento della densità da un valore costante ρ₀ è trascurato ovunque tranne che nel termine rappresentante la spinta di Archimede g(ρ+−ρ₀)k=ρ₀gαT′k nell'equazione del moto: α è il coefficiente volumico di espansione termica e k un versore secondo +z. Le equazioni linearizzate sono pertanto le seguenti:

A queste va aggiunta un'equazione per T′, che è:

dove w′ è la componente z di u′ e κ è il coefficiente di conducibilità termometrica (κ=χ/ρ₀c_p; χ=conducibilità, c_p=calore specifico a pressione costante). Il termine w′ΔT/d rappresenta il moto advettivo del calore, perché c'è un gradiente di temperatura stazionario ΔT/d nella direzione −z.

Le variabili t, x e y non appaiono nell'equazione differenziale e pertanto ci sono dei modi normali contenenti un fattore exp [i(ax+by)+σt]. Per studiare l'instaurarsi della convezione, è sufficiente considerare un moto bidimensionale, nel piano x, z per esempio. Inoltre si può dimostrare che σ è reale; la condizione critica per la stabilità è quindi che sia σ=0. Pertanto possiamo scrivere:

T′=Ø(ζ)e^ikξ (89)

e analogamente per u′, w′ e p′; ξ e ζ sono le coordinate adimensionali ξ=x/d e ζ=z/d, mentre k è il numero d'onda orizzontale. Se si sostituiscono queste espressioni nelle (87) e (88) e si eliminano u′, w′ e p′ si ottiene l'equazione differenziale ordinaria

per la funzione Ø(ξ), ove R_a è il numero di Rayleigh adimensionale

Per ognuna delle due superfici ζ=ζ₀, con ζ₀=0 oppure 1, sono stati considerati due tipi di condizioni al contorno. Per una superficie rigida e che conduca perfettamente il calore, u′, w′ e T′ sono tutte nulle e ne segue che

Per una superficie libera la condizione u′=0 è sostituita dall'annullarsi della componente x, z della tensione viscosa; quindi

e ancora

perché sulla superficie è w′=0.

Ne segue

Si potrebbe pensare che su di una superficie libera P′ debba essere posta uguale a zero. Tuttavia, se la superficie viene spostata di una quantità δ=δ(x) nella direzione z dalla sua posizione z₀ per il fluido stazionario (δ è una piccola quantità del primo ordine), la pressione in z₀ cambia della quantità del primo ordine ρ_ogδ. Lo spostamento non influenza nessun'altra quantità del prim'ordine; quindi il valore di P′ in z₀ deve essere lasciato libero nelle equazioni linearizzate.

Per ogni k fissato, l'equazione differenziale ordinaria (90), con le condizioni al contorno, è un problema agli autovalori per l'autofunzione Ø(ζ) e per l'autovalore R_a. Il problema consiste nello scegliere k in modo da minimizzare R_a. I valori critici di R_a e k ottenuti in questo modo per varie condizioni al contorno sono i seguenti:

Il terzo caso (per il quale il calcolo è particolarmente semplice, essendo l'autofunzione fondamentale semplicemente Ø(ζ)=sen πζ) non è realistico dal punto di vista di un'esperienza da eseguire in laboratorio, ma lo è forse un po' di più per la zona convettiva di una stella, in cui, comunque, il problema interessante non è l'instaurarsi della convezione, ma le proprietà di convezione totalmente turbolenta per valori molto alti di R_a e dove, in ogni modo, le equazioni precedenti non sono valide, perché la compressibilità non può essere ignorata.

La soluzione del modo normale descritta sopra consiste di lunghi vortici paralleli con direzioni di rotazione alternate e assi di rotazione in direzione y. Naturalmente, gli assi possono essere orientati secondo una direzione qualunque e tali soluzioni possono essere sovrapposte, per la linearità delle equazioni (87) e (88), e dare trame di convezione poligonali; per esempio, sovrapponendo sei esponenziali, si ottiene la soluzione seguente:

che rappresenta una convezione in celle esagonali; qui η sta per y/d, in analogia con ξ=x/d e ζ=z/d.

La presenza di celle poligonali, invece che di vortici, all'instaurarsi della convezione, nei primi esperimenti può essere stata causata dall'effetto delle pareti laterali del recipiente o da effetti non lineari che risolvono la degenerazione dei modi ottenuti dalle equazioni lineari.

Attualmente si ritiene che, in un certo intervallo di numeri R_a di Rayleigh al di sopra del valore critico, i vortici siano la forma stabile e che certe strutture poligonali diventino stabili per valori più alti di R_a. La verifica sperimentale è piuttosto delicata, perché R_a va mantenuto costante per un tempo piuttosto lungo in assenza di perturbazioni esterne, per ottenere una struttura stazionaria.

Un ulteriore parametro adimensionale nel problema della convezione è il numero di Prandtl P_a=ν/k. La velocità di formazione o di decadimento di un determinato modo normale dipende sia da R_a che da P_a, ma il valore critico di R_a non dipende da P_a.

b) Zone di convezione nelle stelle.

Le equazioni di equilibrio idrostatico e termico di una stella, supponendo che il materiale sia omogeneo e in quiete, sono

in cui r è la coordinata radiale dal centro della stella, p=p(r) la pressione, ρ=ρ(r) la densità, T=T(r) la temperatura, M=M(r) la massa totale all'interno del raggio r, L=L(r) il flusso di energia uscente da una superficie sferica di raggio r nell'unità di tempo, ε=ε(r) la potenza prodotta da reazioni termonucleari per unità di massa, χ=χ(r) il coefficiente di opacità, a la costante di Stefan-Boltzmann, c la velocità della luce e G la costante di gravitazione universale. Inoltre, le proprietà del mezzo sono legate da un'equazione di stato, da una legge di opacità e da una legge di produzione di energia nucleare, che sono della forma

p=p(ρ, T), χ=χ(ρ, T), ε=ε(ρ, T).

Come si ricava dalla (97) la temperatura diminuisce verso l'esterno; cioè gli strati di gas sono scaldati dal basso e si deve considerare la possibilità di una convezione termica. Se si ha convezione alcune delle equazioni (solo la (97) in pratica) devono essere modificate. In questo caso non si può trascurare la compressibilità e la condizione per l'instabilità (per bassi valori di ν e κ, con le notazioni del È a) è che l'entropia, piuttosto che la temperatura, diminuisca verso l'esterno. Se l'entropia diminuisce verso l'esterno e se un elemento di materia sale e si espande adiabaticamente, si trova a essere meno denso del gas che lo circonda e continua sempre a salire. Se si combina la condizione per l'entropia con l'equazione di stato dei gas perfetti, si trova che il gradiente di temperatura critico è

c_p essendo il calore specifico a pressione costante e g l'accelerazione di gravità locale GM/r². Se il modulo del gradiente di temperatura ∣dT/dr∣, dato dalla (97), supera g/c_p, ha luogo la convezione.

La convezione, trasportando energia verso l'esterno, diminuisce il gradiente di temperatura. Questo fa diminuire il contributo dell'irraggiamento al flusso verso l'esterno, ovvero il valore di L ottenuto risolvendo la (97); quindi L contiene contributi sia dell'irraggiamento, sia della convezione. Nei primi calcoli sulla struttura stellare, si sceglieva come gradiente di temperatura a un raggio r il più piccolo tra i valori forniti dalla (97) e dalla (98). Questo era giustificato in certi casi, per i quali stime approssimative dicevano (v. Schwarzschild, 1958) che una convezione turbolenta molto modesta (con velocità di 30 m/s e differenziali di temperatura di 1 °K) può trasportare energia sufficiente per far determinare il gradiente adiabatico (98) con una precisione assai elevata; reciprocamente, una piccola variazione al disopra del gradiente adiabatico è sufficiente per creare tanta convezione. Era quindi da ritenere che in ogni punto della stella prevalesse o l'equilibrio radiativo o quello convettivo.

Sebbene il procedimento appena descritto sia a volte soddisfacente per la conoscenza della struttura stellare, non lo è da altri punti di vista.

1. Al confine di una zona convettiva i due gradienti (97) e (98) sono uguali; esiste quindi una regione, che può essere abbastanza estesa, in cui il grado di convezione non è conosciuto, nemmeno approssimativamente, per mancanza di una teoria. Un importante effetto della convezione è di mescolare il materiale della stella in quelle regioni in cui si ha convezione. Questo può essere molto importante, per esempio, agli ultimi stadi dell'evoluzione, quando certe specie nucleari in alcune zone si siano esaurite per effetto delle reazioni termonucleari. È stato dimostrato da studi recenti (Jüri Toomre) che piccoli cambiamenti nelle ipotesi fatte su di un modello a lunghezza di mescolamento o su altri modelli di convezione possono variare l'intensità del mescolamento in modo molto drastico, in certi casi.

2. Nel Sole la convezione all'interno e subito al di sotto della fotosfera dà origine alla granulazione, alla supergranulazione e a oscillazioni verticali dell'atmosfera aventi un periodo di cinque minuti. La mancanza di una vera e propria teoria non permette una comprensione completa di questi fenomeni e degli effetti che determinano nei processi che avvengono nella fotosfera.

3. In certi casi, ad esempio negli involucri delle stelle giganti rosse, la convezione può essere molto più violenta di quanto è suggerito dalla nostra descrizione e la validità del metodo dato sopra per calcolare dT/dr è piuttosto dubbia.

4. Nella teoria delle stelle pulsanti c'è un equilibrio molto delicato tra i meccanismi di formazione e di smorzamento delle pulsazioni radiali. Uno dei meccanismi di formazione coinvolge una zona convettiva e non può essere descritto in modo soddisfacente senza una teoria della convezione turbolenta, che, per inciso, in questo caso dovrebbe essere una teoria che consideri la dipendenza temporale; parte del materiale entra ed esce dall'equilibrio radiativo durante il ciclo di pulsazione; interesserebbe sapere, per esempio, il tempo di ritardo per la formazione e il decadimento della convezione.

5. In zone convettive che si trovano in profondità, come quelle che si presentano in certe stelle di tipo A, studiate da Toomre, il materiale è così trasparente al flusso di radiazione che l'energia continuà a essere trasportata in gran parte per irraggiamento, anche dopo l'inizio della convezione; in questo caso il gradiente di temperatura è compreso tra le condizioni della (97) e della (98) e deve essere determinato con un metodo un po' più complicato, in cui il meccanismo di convezione va preso in considerazione, anche se in modo approssimato.

8. Alcuni aspetti analitici del flusso compressibile e non viscoso stazionario.

È riconosciuta l'importanza dei metodi della teoria delle funzioni per comprendere e calcolare flussi stazionari bidimensionali attorno ad ali, in canali, ecc., nell'approssimazione di incompressibilità, e varie generalizzazioni di questi metodi sono di eguale importanza (sebbene siano un po' più complicate) per i flussi compressibili e per quelli a simmetria assiale, compressibili e non. In questo campo c'è stato un grande sviluppo di metodi matematici (v. Bers, 1958); in questa breve rassegna sarà descritta solo una linea di sviluppo, e brevemente: il metodo degli operatori integrali di S. Bergman, così come si applica al flusso subsonico bidimensionale. La speranza è di dare un'idea della natura fisico-matematica dei fenomeni, piuttosto che di spiegare come in pratica si calcolino i flussi in aerodinamica.

a) Rappresentazioni quasi conformi.

Per concretezza, si può pensare al flusso attorno a un'ala (possibilmente fessurata, come in fig. 15), con w=u−iv che tende a w_∞=costante per z=x+iy che tende a ∞. Nel caso di fluido incompressibile, u−iv è una funzione analitica di x+iy e, viceversa, ogni funzione analitica rappresenta un flusso. Questo è vero anche per il caso subsonico compressibile, tranne per il fatto che la funzione analitica deve essere sottoposta a una certa distorsione sistematica con un procedimento che dipende dall'equazione di stato e dal numero di Mach M_∞ (=∣w_∞∣/c_∞〈1), ma che non dipende dalla scelta della funzione analitica da cui si è partiti. La distorsione può essere effettuata con una trasformazione odografa, come risultato della quale il flusso viene a essere descritto da equazioni differenziali lineari, così che la distorsione è descritta da un operatore lineare, precisamente dall'operatore integrale di Bergman, di cui si dirà più avanti. La funzione distorta (prima o dopo la trasformazione odografa) determina una cosiddetta rappresentazione quasi conforme ed è detta funzione quasi conforme. Ogni rappresentazione quasi conforme è soluzione di un sistema del second'ordine uniformemente ellittico di equazioni a derivate parziali (nel caso particolare del flusso incompressibile, in cui la rappresentazione è conforme, queste sono le equazioni di Cauchy-Riemann); viceversa, ogni soluzione del sistema ellittico dà una rappresentazione quasi conforme. Il principio di massimo e il principio di massimo modulo valgono per queste funzioni; da questo segue l'unicità della soluzione delle equazioni di flusso sotto opportune condizioni (condizioni al contorno, condizioni all'infinito e, per ogni parte dell'ala, la condizione di Kutta-Žukovskij o il valore della circolazione; v. Bers, 1958).

Il metodo di Bergman presenta il vantaggio che il calcolo numerico riguarda solo linee e curve nel piano. Ci si può permettere di prendere punti distanziati di piccoli intervalli su queste linee e curve e si possono usare metodi accurati, come le integrazioni di Runge-Kutta e i procedimenti di interpolazione; al contrario, la soluzione delle equazioni a derivate parziali coi metodi a differenze finite su un reticolo bidimensionale è intrinsecamente grossolana, inaccurata e richiede molto tempo.

Occorre comunque, a questo punto, precisare cosa debba intendersi per rappresentazione quasi conforme. A questo scopo, sia data una rappresentazione z→ω(z)=ϕ(x, y)+iψ(x, y) di una regione R_z del piano z su di una regione R_ω di un piano ω. Piccoli cerchi vengono trasformati da ω in piccole ellissi. (Si possono facilmente formulare queste ipotesi in modo più preciso, se si vuole). Se esiste un numero Q(≥1) tale che, per ogni z di R_z,

allora la rappresentazione ω e la funzione ω(z) sono dette ‛Q quasi conformi'. Se è Q=1, la rappresentazione è conforme e ϕ+iψ è una funzione analitica di x+iy.

I seguenti esempi di flussi bidimensionali sono dati senza dimostrazione (i simboli hanno il loro significato usuale):

b) Le equazioni del flusso.

Poiché l'entropia è costante molto a monte ed è costante lungo ogni linea di corrente, l'intero flusso è isoentropico. Quindi, in base al teorema di Kelvin (v. sopra, cap. 2, È g), esso è irrotazionale, tranne che in uno strato limite, che supporremo essere di spessore trascurabile, e nel vortice staccato che è stato lasciato a valle quando l'ala ha cominciato il moto. Quindi, se x e y sono coordinate cartesiane del sistema di riferimento solidale con l'ala e se u e v sono le corrispondenti componenti della velocità, allora è:

vorticità=v_x-u_y=0, (99)

in cui gli indici in basso, x e y, stanno ad indicare l'operazione di derivazione parziale. L'equazione di continuità ∇•(ρv)=0 diventa

(ρu)_x+(ρv)_y=0. (100)

La legge di Bernoulli è valida su una linea di corrente e, poiché molto a monte p, ρ e u hanno il medesimo valore su tutte le linee di corrente, si ha:

dove q²=u²+v² e p₀ è la pressione nel punto di ristagno. Si noti che dalle (99-101) segue l'equazione di Eulero (v•∇)v+(1/ρ)∇p=0. Essendo il flusso isoentropico, p è una funzione di ρ e la (101) stabilisce una relazione tra ρ e q, che scriveremo ρ=ρ(q). Pertanto dalla (101) segue che la velocità locale c del suono e il numero di Mach locale M=q/c sono, in funzione di q, date da:

Nel caso speciale di un gas perfetto, per cui p/p₀=(ρ/ρ₀)^γ (γ=costante~1,4 per l'aria), c²=γp/ρ e c²₀=γp₀/ρ₀, le funzioni ρ(q) e M(q) sono date da:

in unità tali che ρ₀=1, c₀=1 (quindi p₀=1/γ).

Le equazioni (99) e (100) indicano che il flusso può essere scritto in funzione di un potenziale ϕ o di una corrente ψ, secondo le notazioni seguenti:

Se nella (100) si esprimono le velocità in funzione del potenziale ϕ e se le derivate di ρ che vi compaiono si esprimono nel modo seguente:

e analogamente per la derivata ∂ρ/∂y, si trova, utilizzando la (102), che

Questa equazione non è lineare, perché u, v e c dipendono da q: essa è di tipo ellittico nelle parti del flusso in cui è M²=q²/c²〈1 (regioni subsoniche) e di tipo iperbolico dove è M²>1 (regioni supersoniche). Nel nostro problema è sempre M²〈1.

c) La trasformazione odografa.

Nella cosiddetta trasformazione odografa x e y sono sostituite, come variabili indipendenti, da u e v; le variabili dipendenti sono quindi x, y, ϕ e ψ. Poiché i coefficienti nella (108) dipendono solo da u e v, si ottengono delle equazioni differenziali lineari. Questo può essere fatto, per una data soluzione, nelle vicinanze di un punto x, y in cui lo jacobiano

sia diverso da 0. Si può dimostrare che per un flusso subsonico, escluso il caso banale in cui u e v siano costanti, J può avere solo zeri isolati.

Per ogni punto in cui sia J≠0, esiste un intorno in cui x e y sono funzioni a un sol valore di u e v. Invece di provare a fare direttamente la trasformazione (108), si procede riscrivendo prima le (106) e (107) nel modo seguente:

Si riscrivono i primi membri di queste equazioni secondo: ϕ_udu+ϕ_vdv e ψ_udu+ψ_vdv; poi si risolvono le equazioni per ottenere dx e dy nella forma E du+F dv. Questi devono essere differenziali esatti, perché x e y sono funzioni di u e v. Otteniamo quindi due equazioni (condizioni di compatibilità) del tipo: E_v=F_u. Per arrivare a questo, conviene scrivere

u+iv=qe^iϑ; (111)

q e ϑ sono così coordinate polari nel piano u, v, detto anche ‛piano odografo'. Dalla (110) si ottiene

e la condizione di compatibilità è

Effettuando le differenziazioni e separando la parte reale dall'immaginaria si ottengono le equazioni odografe

che, come previsto, sono lineari: cioè, i coefficienti dipendono solo dalle variabili indipendenti q, ϑ, anzi solo da q. Se si eliminano successivamente ψ e ϕ dalle (112) e (113) si ottengono due equazioni lineari del second'ordine

Queste equazioni sono state ottenute da Chaplygin nel 1904.

d) Il metodo di Bergman.

Se si sostituisce q con una nuova variabile λ=λ(q), data da

l'equazione per il potenziale si riduce a:

ϕ_ϑϑ+ϕ_λλ+Λ(λ)ϕ_λ=0, (117)

in cui

L'equazione per la corrente è:

ψ_ϑϑ+ψ_λλ−Λ(λ)ψ_λ=0. (119)

Il metodo di Bergman si applica a equazioni del tipo (117) e (119). Nella (116) q_cr è la cosiddetta velocità critica, soluzione dell'equazione M(q)=1. Flussi con q>q_cr sono supersonici, perché q>c(q), c(q) essendo la velocità del suono; flussi con q〈q_cr sono subsonici, perché in questo caso q〈c(q).

Generalmente non si riesce a esplicitare la funzione Λ(λ); invece si danno sia Λ che λ in funzione della variabile m=M². Per un gas perfetto, si possono esprimere ρ e q in funzione di m usando la (104) e la (105). La (116) dà allora:

da cui:

e dalla (118) si ottiene:

A seconda del segno della (116) un flusso subsonico è descritto da una soluzione della (117) o della (119) in una regione nella metà sinistra del piano λ, ϑ.

A volte si effettua un ulteriore cambiamento nella variabile dipendente, ma l'equazione risultante ha la stessa forma. Bergman ha dimostrato che la soluzione generale della (117) è:

in cui è Z=λ−iϑ, Φ₀(Z) è una funzione analitica arbitraria e le altre sono date, per induzione, da

Φ_n(Z)=−½Φ_n-1(Z). (124)

Le G_n(λ) sono funzioni universali, per una data equazione di stato, e, per λ〈0, si ottengono per induzione da

G₀=1, Gn′₊₁=Gn″+ΛG_n. (125)

Usando iterativamente la (123) nella forma integrale, si ottiene:

Quindi, scrivendo ϕ(Z) per ϕ(λ, ϑ), le (123) e (126) ci danno:

dove

Le serie che compaiono nelle (123) e (128) convergono all'interno di un certo angolo, che si estende all'infinito nella metà sinistra del piano λ, ϑ. Anche in tal caso, però, è spesso necessario effettuare un prolungamento analitico. Si noti che K non è una funzione analitica di Z perché nella (128) appare esplicitamente λ=Re(Z).

La (127) è l'equazione di Bergman per la funzione deformata ϕ(Z) in termini della funzione analitica Φ₀(Z). Se Φ₀(Z) rappresenta un flusso incompressibile attorno a una data sezione alare, ϕ(Z) rappresenta il flusso compressi- bile attorno a una sezione simile.

Per un flusso asimmetrico incompressibile, l'equazione del potenziale

ha la stessa forma della (117) e può quindi essere trattata con una piccola variante del metodo di Bergman (v. Bergman, 1966, e la bibliografia ivi riportata).

9. Problemi a valori iniziali per il flusso compressibile.

In questa sezione discuteremo i problemi a valori iniziali del flusso non viscoso. Per gli ultimi lavori matematici sui problemi corrispondenti del flusso viscoso si rinvia il lettore a Ladyženskaja (v., 1963).

a) Il problema di Riemann.

Il prototipo dei problemi che consideremo è il problema di Riemann del flusso unidimensionale, a partire da uno stato iniziale in cui u, ρ e p (velocità, densità e pressione) hanno valori costanti: u₁, ρ₁ e p_i per x>0 e u₂, ρ₂ e p₂ per x〈0. Un esempio è fornito dal tubo a urto (shock tube), in cui un sottile diaframma attraverso il tubo separa aria ad alta pressione p₂, sulla sinistra, dall'aria a pressione più bassa p₁ sulla destra (v. fig. 16). All'istante t=0 il diaframma viene rotto o rimosso. Un'onda d'urto avanza allora verso destra e un'onda di rarefazione verso sinistra, com'è indicato schematica mente nella fig. 17, dove la pressione è rappresentata in funzione di x, a un istante t>0.

Si suppone un'equazione di stato ideale, per cui le velocità del suono sono c₁=√-γ-p-₁-/-ρ-₁ alla destra e c₂=√-γ-p-₂-/-ρ-₂ alla sinistra dell'onda di rarefazione. Si suppone che il sistema fosse in equilibrio meccanico e termico in tempi precedenti il tempo t=0; quindi u₁=u₂=0 e p₁/ρ₁=p₂/ρ₂ (legge di Boyle). La linea tratteggiata della fig. 17 indica la linea di separazione, per t>0, tra il gas che era inizialmente ad alta pressione e quello che era a pressione bassa. Questa separazione è detta ‛discontinuità di contatto'. Per t>0, la pressione è costante attraverso di essa, ma non la densità: il gas a destra è stato scaldato dall'urto, mentre quello a sinistra è stato raffreddato dall'espansione adiabatica nell'onda di rarefazione. Si suppone di poter trascurare il flusso di calore attraverso questa superficie di separazione.

Nella formulazione del problema non compare nessun parametro avente le dimensioni di una lunghezza; vale quindi un principio di similitudine e le grandezze del flusso dipendono da x e t solo attraverso il rapporto ξ=x/t. Le posizioni dell'urto, della discontinuità di contatto, dell'inizio e della fine dell'onda di rarefazione sono ξ₀, ξ₁, ξ₂ e ξ₃. Tutta l'aria compresa tra ξ₂ e ξ₀ si muove con velocità costante u=ξ₁. La velocità dell'urto, ξ₀, e la velocità del fluido che lo segue, u=ξ₁, si ottengono, in funzione del rapporto tra i valori delle densità η=ρ₀/ρ₁ nel punto dell'urto, dalle condizioni di Rankine-Hugoniot discusse nel cap. 2 (equazioni 14, 15 e 18):

Il fronte dell'onda di rarefazione si muove esattamente con la velocità del suono: ξ₃=−c₂.

Resta da discutere l'onda di rarefazione nei particolari. Una volta fatto questo, le condizioni di continuità della velocità e della pressione in ξ₂ ci forniranno le equazioni ulteriori per determinare tutte le incognite. Se f è una grandezza qualsiasi che dipende da ξ=x/t, si ha:

Pertanto, le prime due equazioni di Eulero (6) danno:

mentre la legge dell'entropia dà:

Queste equazioni vanno risolte con le condizioni al contorno sul fronte dell'onda di rarefazione in ξ=ξ₃=−c₂; p=p₂ e u=0. La soluzione si calcola rapidamente ed è:

Si vede che nell'onda di rarefazione u varia linearmente con la distanza, mentre i grafici di p(ξ) e di ρ(ξ) sono concavi verso l'alto, come appare nella fig. 17 per p(ξ).

In termini delle funzioni date dalle (135), (136) e (137) le condizioni di continuità in ξ=ξ₂ sono:

u(ξ₂)=ξ₁, (138)

p(ξ₂)=p₀, (139)

ρ(ξ₂)=ρ0′. (140)

Si possono risolvere le quattro equazioni (129), (131), (138) e (139), numericamente o graficamente, rispetto alle quattro incognite ξ₁, ξ₂, p₀ e η. La velocità dell'urto ξ₀ e la densità minima ρ0′ sono allora date dalla (130) e dalla (140), rispettivamente.

Per inciso, si noti che, se è p₁=ρ₁=0, come nel caso in cui l'espansione del gas avvenga nel vuoto, l'onda di rarefazione si estende sulla destra fino al punto in cui ρ(ξ) e p(ξ) sono nulle nelle (136) e (137); in quel punto la velocità del fluido è

che è detta ‛velocità di fuga'.

Abbiamo usato le equazioni differenziali nell'onda di rarefazione, ma esse sono chiaramente valide anche nelle regioni in cui le grandezze proprie del flusso sono costanti. Si può dimostrare che la soluzione così ottenuta è unica; cioè che l'insieme delle funzioni differenziabili a tratti date sopra, p(x, t), ρ(x, t) e u(x, t), è l'unico insieme di questo tipo che soddisfi le condizioni seguenti: a) le condizioni iniziali; b) le condizioni di Rankine-Hugoniot per ogni onda d'urto; c) l'assenza di urti negativi; d) la continuità della pressione e della velocità attraverso tutte le discontinuità di contatto (dove densità, entropia e temperatura possono essere discontinue); e) la continuità di tutte le grandezze del flusso attraverso la testa e la coda di ogni onda di rarefazione; f) le equazioni a derivate parziali nel resto dello spazio.

Gli altri casi del problema di Riemann (con valori iniziali generici u₁, p₁, ρ₁ e u₂, p₂, ρ₂) sono analoghi. Secondo i casi, ci possono essere due onde di rarefazione, due urti, o un urto e un'onda di rarefazione. In ogni caso l'esistenza e l'unicità della soluzione del problema a valori iniziali sono state dimostrate sotto le condizioni elencate sopra; queste condizioni equivalgono, per un fluido, alle leggi fondamentali di conservazione e alla seconda legge della termodinamica.

Il problema di Riemann può essere generalizzato supponendo che, inizialmente, in entrambe le regioni con x>0 e x〈0 le funzioni u(x, 0), p(x, 0) e ρ(x, 0) siano regolari (diciamo analitiche) ma non necessariamente costanti; si suppone ancora che abbiano discontinuità semplici in x=0. È presumibile allora che la soluzione sia simile, almeno entro un certo intervallo temporale o≤t≤t₀, alla soluzione del problema di Riemann corrispondente, se si eccettua il fatto che le varie discontinuità viaggeranno su curve del piano x, t, invece che su linee rette.

Nel problema generalizzato non si può, di solito, prendere come intervallo [0, t₀] l'intervallo [0, ∞], a meno che non si preveda la possibilità che insorgano fenomeni del tipo della generazione spontanea di urti, a cui si fa cenno nel seguito.

b) Curve caratteristiche, il teorema di Cauchy-Kovalevskaja.

Sebbene l'idea generale delle caratteristiche risalga perlomeno a Riemann, qui la discuteremo brevemente per l'importanza che essa riveste nel problema non ancora risolto della formulazione corretta dei problemi ai valori iniziali nella dinamica dei fluidi.

Ricordiamo che la soluzione generale delle equazioni delle onde

è:

dove f e g sono funzioni arbitrarie di classe C¹. Per valori iniziali arbitrari u(x, 0) e v(x, 0), la soluzione delle (141) è unica e si ottiene ponendo

f(x)=½u(x, 0)+½v(x, 0)

g(x)=½u(x, 0)−½v(x, 0).

Le famiglie di linee nel piano x, t date da x−ct=cost e da x+ct=cost sono dette caratteristiche progressive e regressive, rispettivamente. L'informazione viaggia lungo queste linee, nel senso che, se il valore di u−v è noto in un punto qualsiasi di una caratteristica progressiva (o u+v in un punto qualsiasi di una caratteristica regressiva), il suo valore è noto in ogni punto successivo di quella caratteristica e, precisamente, esso è lo stesso, poiché u−v dipende solo da x−ct.

L'importanza di questo flusso d'informazione per il problema a valori iniziali è la seguente. Supponiamo che i valori ‛iniziali' di u e v non siano dati al tempo t=0, ma su di un'altra linea x+at=b del piano. In generale, il problema ha ancora una soluzione unica, ottenuta mediante una semplice modifica del metodo precedente. Tuttavia, se la linea x+at=b coincide con una caratteristica (cioè, se a=±c), allora, in generale, sia l'esistenza che l'unicità della soluzione sono perse. Più precisamente, prendendo il caso di a=c, non esiste soluzione, a meno che i valori dati di u e v non soddisfino la condizione di compatibilità che u+v sia costante su quella linea; se questa condizione è soddisfatta, la soluzione non è unica, perché u+v può avere qualsiasi altro valore arbitrario sulle altre caratteristiche regressive.

Per un generico problema iperbolico di ordine m, ci sono m famiglie di caratteristiche sul piano x, t. In generale sono curve, se l'equazione differenziale ha coefficienti variabili, e inoltre dipendono dalla soluzione stessa, se le equazioni non sono lineari. Sono caratterizzate dalla proprietà che le m funzioni (variabili dipendenti) non possono essere date arbitrariamente lungo di esse, ma sono soggette a condizioni di compatibilità, come nell'esempio precedente della propagazione ondosa.

Le equazioni di Eulero sono del tipo

dove U è un vettore di componenti u, ρ, p, mentre A è una matrice 3×3 con gli elementi dipendenti da u, ρ, p. (Si suppone che l'energia specifica interna sia stata eliminata mediante un'equazione di stato ε=ε(p, ρ)). Un sistema del tipo (143) è detto iperbolico se la matrice ha tutti gli autovalori reali e un insieme completo di autovettori (il realizzarsi di queste condizioni può dipendere da x e t e dalla soluzione che si considera, dato che A dipende da u, ρ e p). Si può dimostrare che le equazioni di Eulero sono del tipo iperbolico. Poiché A possiede un insieme completo di auto- vettori, esiste una matrice T tale che TAT^-1 è diagonale, per cui (TA )_jk=λ_jT_jk, dove λ_j sono gli autovalori. Se si moltiplica la (143) alla sinistra per T, si ottiene:

Nella j-esima equazione tutte le derivazioni sono lungo una curva x_j(t) del piano x, t, che è la j-esima caratteristica, data da

le funzioni U₁, U₂, ... non possono quindi essere date arbitrariamente lungo la curva, ma sono soggette alla condizione di compatibilità di soddisfare la j-esima delle equazioni (144), che ha il carattere di un'equazione differenziale ordinaria lungo la curva. Poiché A dipende dalle U_j che a loro volta dipendono da x e t, le λ_j dipendono da x e t e la (145) va interpretata come:

variando la costante d'integrazione si ottiene una famiglia di curve. Si dice che le equazioni (144) sono messe in ‛forma caratteristica'.

Il modo più semplice per porre le equazioni della fluido- dinamica unidimensionale in forma caratteristica è di scegliere la densità ρ, la velocità u e l'entropia specifica S come variabili dipendenti. Se si scrive l'equazione di stato p=p(S, ρ) e se si definisce c=c(S, ρ) attraverso la

le equazioni (6) di Eulero diventano:

Si noti che la terza di queste equazioni è già in forma caratteristica e che i cammini delle particelle formano una famiglia di caratteristiche, lungo ognuna delle quali l'entropia è costante. La matrice A di questo sistema è

i suoi autovalori λ₁, λ₂ e λ₃ sono le radici dell'equazione:

det(A−λΙ)=[(u−λ)²−c²](u−λ)=0,

cioè λ=u±c e u. Le caratteristiche sono le traiettorie dei segnali sonori progressivi e regressivi e delle particelle di fluido. Si trova rapidamente che le equazioni in forma caratteristica sono:

Un importante caso particolare è quello in cui l'entropia è costante a un certo istante iniziale. L'ultima delle equazioni precedenti ci dice allora che S è sempre costante (finché non s'incontrano urti). Allora p e c dipendono solo da ρ e scriveremo p(ρ) e c(ρ). Se si definisce una nuova grandezza termodinamica:

le prime due equazioni delle (146), dopo essere state divise per ρc, danno

Le quantità σ±u, che sono dette ‛invarianti di Riemann', sono costanti lungo le caratteristiche di entrambi i tipi.

Si è visto che, se una curva del piano x, t, sulla quale si desiderano specificare i dati iniziali, coincide con una caratteristica, in generale si perdono l'esistenza e l'unicità della soluzione. All'altro estremo, se tale curva non è mai caratteristica (cioè non è mai tangente a una caratteristica), allora esistenza e unicità sono garantite in un qualche intorno della curva, cioè in una striscia del piano x, t che contiene la curva. Questo è il noto teorema di Cauchy-Kovalevskaja. (Per una formulazione più precisa e dettagliata, v. Courant e Hilbert, 1962; v. Courant e Friedrich, 1948). Il teorema si applica a sistemi del tipo (143), siano essi iperbolici o no. Se alcuni degli autovalori della matrice A non sono reali, si dice che le caratteristiche corrispondenti sono non reali; l'ipotesi del teorema di CauchyKovalevskaja è che la curva iniziale non sia mai tangente a una caratteristica reale.

Si noti che il fatto che una curva iniziale sia o non sia caratteristica dipende non solo dalla curva, ma anche dai dati iniziali sulla curva, perché le direzioni caratteristiche sui punti della curva sono determinate dagli autovalori della matrice A, che, a loro volta, dipendono dai valori di u, ρ e p sulla curva stessa.

Consideriamo adesso il caso particolare delle equazioni di Eulero, con i dati iniziali su una curva parallela all'asse x, a t=t₀. Si è visto che le caratteristiche rappresentano segnali che viaggiano con velocità dx/dt=u, u+c, u−c. Per dati iniziali ragionevoli, cioè limitati, queste velocità sono sempre finite; le caratteristiche non possono quindi mai essere tangenti alla linea t=t₀, poiché questo implicherebbe una velocità infinita di propagazione del segnale. Se ne conclude che il teorema di Cauchy-Kovalevskaja vale per il problema a valori iniziali nella parte regolare del flusso (dove non ci sono urti), se i dati sono forniti su di una linea t=t₀, e quindi che esiste un'unica soluzione in un certo intervallo t₀≤t≤t₁. Se si associa questo risultato a quello dato nel È a per il problema di Riemann, sembrerebbe ragionevole ritenere che un problema a valori iniziali, regolare a tratti, abbia un'unica soluzione regolare a tratti in un certo intervallo t₀≤t≤t₁, purché si impongano le sei condizioni che sono elencate nel È a. Questo non implica che il numero di tratti regolari della soluzione, come funzione di x, sia lo stesso per t>t₀ che per t=t₀. Già nel problema del tubo a urto, descritto precedentemente, c'erano due tratti analitici (costanti) per t =0 e cinque tratti per t>0; inoltre, come mostreremo nel È c, gli urti si possono formare spontaneamente durante il flusso; per di più, la collisione o la coalescenza di due urti può produrre una discontinuità di contatto.

A seguito di lavori recenti, dovuti specialmente a J. Glimm e a P. D. Lax, sembra ora molto probabile che la congettura precedente sia vera, anche con l'intervallo [t₀, t₁] esteso a [t₀, ∞], sotto ipotesi molto ragionevoli sui dati iniziali. (Per una rassegna sullo stato attuale del problema a valori iniziali, v. Lax, 1973).

Del problema corrispondente in due o tre dimensioni dello spazio non si sa quasi niente; faremo comunque qualche osservazione nel È d.

c) Generazione spontanea di urti.

Supponiamo che un pistone, muoventesi con una velocità che cresce continuamente da zero, sia spinto in un tubo contenente un gas inizialmente a riposo a pressione e volume costanti, come indicato nella fig. 18. A un certo momento si forma un urto; fino a quell'istante il flusso è isoentropico e può essere analizzato col metodo degli inva- rianti di Riemann, usando l'equazione (148). Sulle caratteristiche regressive σ−u è costante e ha lo stesso valore costante, precisamente il valore iniziale, su tutte; di conseguenza σ−u rimane costante per tutto il flusso, fino alla formazione dell'urto. Analogamente anche σ+u, su ogni data caratteristica progressiva, è costante; su ogni caratteristica progressiva sono quindi costanti tutte le grandezze, comprese c, p, ρ, u, ecc. Ogni caratteristica progressiva è pertanto una retta, avendo una pendenza costante (u+c)^-1. Sulle caratteristiche successive che partono dal pistone i valori di σ+u sono successivamente più grandi e le pendenze sono via via più piccole, così che le caratteristiche progressive si devono incontrare in un punto del flusso. In quel punto cessa il flusso regolare (σ+u non può avere più valori) e si genera un urto, la cui intensità è inizialmente zero e poi cresce, dapprincipio con la radice quadrata del tempo successivo alla formazione. È possibile che si formino nel flusso due o più urti in posizioni e istanti differenti, a seconda del moto del pistone.

d) Osservazioni sui casi multidimensionali; dipendenza continua dai dati iniziali.

Nel generalizzare la congettura espressa alla fine del È b al caso con due o tre variabili spaziali, la condizione di ‛differenziabilità a tratti' si muta in quella di ‛analiticità a tratti', per motivi che spiegheremo qui sotto. Un po' grossolanamente, le funzioni iniziali o le funzioni della soluzione sono dette analitiche a tratti se lo spazio, o lo spazio-tempo, può essere diviso in celle in ognuna delle quali le funzioni sono analitiche. Si suppone che i contorni delle celle siano superfici analitiche che s'incontrano secondo curve analitiche. Questa definizione è intenzionalmente vaga per quel che riguarda il tipo di singolarità permesso (per le funzioni sul contorno delle celle, o per le superfici ai loro contorni), dato che per il momento non siamo in grado di formulare ipotesi precise. Probabilmente, anche l'ipotesi che le funzioni della soluzione siano limitate è troppo forte, dato che, per esempio, un urto sferico di implosione produce una pressione infinita nel centro all'istante del collasso. Entro questi limiti, quindi, l'ipotesi è che un problema a valori iniziali, analitico a tratti, di un flusso non viscoso compressibile abbia un'unica soluzione analitica a tratti, purché siano soddisfatte le sei condizioni date nel È a, opportunamente generalizzate per il caso multidimensionale.

Per un problema a valori iniziali ben posto, nel senso di Hadamard, non solo deve esistere un'unica soluzione per ogni stato iniziale consentito, ma la soluzione deve dipendere con continuità, in qualche modo, dallo stato iniziale. L'instabilità di Helmholtz fornisce un esempio di dipendenza discontinua dallo stato iniziale: una superficie piana separa due regioni in ognuna delle quali un fluido è in moto uniforme, con slittamento (supposto senza attrito) sul piano. Introducendo una piccola perturbazione nei dati iniziali, sotto forma di una leggera corrugazione sinusoidale della superficie e di una corrispondente modifica del flusso vicino a essa, si può ottenere una soluzione in cui l'ampiezza della perturbazione cresce esponenzialmente col tempo, fintanto che l'ampiezza stessa è piccola rispetto alla lunghezza d'onda (supponendo o che i fluidi siano incompressibili o che la velocità di slittamento non superi una certa frazione delle velocità del suono). Inoltre, la velocità di crescita esponenziale di questa perturbazione cresce senza limite, al tendere a zero della lunghezza d'onda λ della corrugazione. Pertanto, per ogni ε>0 e ogni M>0, esiste un valore di λ abbastanza piccolo perché una perturbazione iniziale, sufficientemente piccola, di lunghezza d'onda λ cresca di un fattore M in un tempo minore o uguale a ε; la soluzione non dipende quindi con continuità dai dati iniziali.

Se c'è una tensione superficiale o d'interfaccia tra i due fluidi, le corrugazioni con lunghezza d'onda minore di un certo λ₀ sono stabili ed è ripristinata la dipendenza continua dai dati iniziali, nonostante che le lunghezze d'onda maggiori siano ancora instabili.

Senza la tensione superficiale, bisogna che la superficie iniziale sia analitica perché esista una soluzione. Consideriamo adesso il caso di una superficie iniziale analitica a tratti. Un caso semplice è quello costituito da una corrugazione formata da strisce piane e parallele che s'incontrano alternativamente ad angoli concavi e convessi, in modo che la sezione della superficie sia a zig-zag. L'analisi dell'instabilità mediante il metodo delle serie di Fourier non è qui applicabile nemmeno per ampiezze molto piccole, perché, nonostante che la funzione che descrive la superficie iniziale abbia una serie di Fourier convergente, la sostituzione nelle equazioni del moto dà una serie che diverge per ogni valore di t>0. Ciò nonostante sembra verosimile che questo problema rientri nell'ipotesi precedente e che una soluzione esista, ma la natura della soluzione è completamente sconosciuta.

10. Metodi di calcolo.

Lo sviluppo dei metodi di calcolo nella fluidodinamica è stato molto rapido e generale a partire da circa il 1950, quando si sono resi disponibili grandi calcolatori elettronici e quando le richieste di finanziamenti da parte delle industrie aeronautiche, spaziali, nucleari e chimiche hanno cominciato a essere soddisfatte. Qui descriveremo alcuni esempi di metodi, per illustrare la portata delle tecniche implicate. Ometteremo gli eleganti metodi analitico- numerici atti a trattare il flusso compressibile, perché uno di essi, il metodo dell'operatore integrale di Bergman, è già stato descritto brevemente nel cap. 8.

Nonostante la rapidità e le dimensioni di questo sviluppo, l'autore ritiene che i metodi esistenti facciano un uso molto inefficiente e inefficace dell'analisi matematica e delle potenzialità dei moderni calcolatori. Questa è indubbiamente una delle maggiori sfide poste alla matematica applicata.

a) Metodi a differenze finite per un flusso non viscoso e compressibile dipendente dal tempo.

Il successo dei metodi classici a differenze finite ottenuto nel campo delle equazioni differenziali ordinarie ha portato naturalmente allo sviluppo di metodi analoghi per le equazioni a derivate parziali della fluidodinamica (e per equazioni simili che s'incontrano in altri rami della fisica dei mezzi continui). In questo paragrafo considereremo solo flussi regolari, senza urti.

Consideriamo, per esempio, un problema a valori iniziali delle equazioni unidimensionali di Eulero (6). Si scelgono piccoli incrementi Δx e Δt e si costruisce un reticolo rettangolare di punti x_j=jΔx e tⁿ=nΔt nel piano x, t. Se f(x, t) è una qualunque delle grandezze caratterizzanti il flusso, u, ρ, p o ε, denoteremo con fn_j il suo valore al punto j, n del reticolo (cioè il suo valore approssimato ottenuto dal calcolo). Le derivate nell'equazione (6) sono sostituite da rapporti incrementali, per es. ∂f/∂t è sostituita da

oppure da

oppure da

o, a volte, da un'espressione più accurata. Se questo è fatto in modo adeguato, ne risulta un sistema di equazioni che, insieme con opportune condizioni al contorno (per esempio a j=±J), può essere risolto rispetto alle grandezze del flusso all'istante tⁿ⁺¹ (per tutti gli x_j), se queste sono note all'istante tⁿ e prima. L'iterazione di questo procedimento, che costituisce un ciclo del calcolo, a partire dai valori noti a t⁰ (e possibilmente anche a t¹ o t^-1), fornisce una soluzione approssimata del problema ai valori iniziali.

Esistono molti modi diversi di approssimare un sistema di equazioni differenziali dato con equazioni a differenze finite: essi hanno proprietà completamente diverse dal punto di vista della stabilità, della precisione e della risolubilità. Il lettore è rimandato a Richtmyer e Morton (v., 1967) per un'analisi dettagliata.

Esistono due tipi principali di sistemi a differenze finite. Nei cosiddetti ‛sistemi espliciti' ognuna delle quantità incognite (cioè i valori delle funzioni all'istante tⁿ⁺¹) è data da una sola equazione. Un sistema per le equazioni di Eulero è, schematicamente, il seguente:

un_j⁺¹=... (j=0, ±1, ...)

ρn_j⁺¹=... (j=0, ±1, ...)

εn_j⁺¹=... (j=0, ±1, ...)

dove i puntini stanno per grandezze che dipendono solo dai valori agli istanti tⁿ e t^n-1. pn_j⁺¹ si ottiene poi dall'equazione di stato. Più in generale, se si risolvono le equazioni nell'ordine indicato, ρn_j⁺¹ potrebbe dipendere dai valori di u all'istante tⁿ⁺¹, ma dai valori delle altre grandezze solo agli istanti tⁿ e t^n-1; analogamente εn_j⁺¹ potrebbe dipendere dai valori di u e ρ all'istante tⁿ⁺¹, ma non da quelli di ε né di p. Nei ‛sistemi impliciti' le incognite appaiono in equazioni del tipo

A_jun_j+₊¹₁+B_jun_j⁺¹+C_jun_j+_-¹₁=... (j=0, ±1, ...), (149)

dove A_j, B_j e C_j sono coefficienti noti. Queste equazioni devono essere risolte come un sistema simultaneo. Con le condizioni al contorno ci sono J₀ equazioni in J₀ incognite (per ognuna delle grandezze u, ρ, ε), J₀ essendo il numero di punti del reticolo spaziale. Normalmente, esse sono lineari, come prima, perché le equazioni a derivate parziali sono quasi lineari e la loro matrice è tridiagonale, così che esse possono essere risolte con un semplice algoritmo (v. Richtmyer e Morton, 1967). Un vantaggio dei sistemi impliciti è discusso qui sotto.

Una caratteristica matematica importante delle equazioni a differenze parziali è stata scoperta da Courant, Friedrichs e Lewy nel 1928. Essi hanno dimostrato che il metodo a differenze finite attualmente più comune per l'equazione delle onde (che può essere considerata il prototipo delle equazioni di Eulero per il moto dei fluidi) è solo condizionatamente stabile, nel senso che, se è c Δt>Δx, la dipendenza continua della soluzione dai dati iniziali si perde in maniera piuttosto catastrofica. Piccoli errori vengono amplificati molto velocemente ed entro pochi cicli la soluzione perde ogni somiglianza con la soluzione dell'equazione differenziale. E non si tratta di errori di arrotondamento, ma di errori che sono inerenti al procedimento stesso delle differenze finite. Questo fenomeno è chiamato instabilità, ma è diverso dall'instabilità delle equazioni a differenze finite ordinarie perché è coinvolto il rapporto c Δt/Δx e restringere il reticolo non serve a niente finché non si diminuisce tale rapporto. È diverso dall'instabilità di un sistema meccanico, in cui ha luogo uno scostamento ordinato e a volte lento dall'equilibrio; in effetti, capita spesso di voler calcolare il comportamento di un sistema fisico instabile. La condizione c Δt=Δx è critica. Se Δt è più piccolo di qualche unità per cento, il calcolo procede regolarmente e indefinitamente; se Δt è più grande di qualche unità per cento, l'instabilità si presenta dopo pochi cicli.

Quando lo sviluppo dei calcolatori moderni, verso la fine degli anni quaranta, rese possibile l'applicazione dei metodi a differenze finite alle equazioni a derivate parziali in problemi pratici, si scopri che l'instabilità può presentarsi in una gran varietà di metodi a differenze finite per equazioni a derivate parziali di ogni tipo. Il criterio di von Neumann per la stabilità, che venne introdotto in quell'epoca, si basava in modo piuttosto intuitivo su di un'analisi di Fourier delle perturbazioni locali a brevi lunghezze d'onda ed è tuttora usato quasi universalmente nei calcoli pratici. Tentativi di dare alle considerazioni di stabilità una base matematica hanno portato a un vasto campo di argomentazioni teoriche. La maggior parte di queste teorie è troppo complicata per essere utile nella pratica, ma alcune idee utili ne sono risultate. Una di queste è quella della dissipazione in uno schema a differenze. Dapprincipio la dissipazione veniva evitata ogni qual volta possibile, ma adesso si è riconosciuto che, in certe circostanze, può essere più utile che dannosa. In base a un teorema di Kreiss (v. Richtmyer e Morton, 1967), uno schema a differenze per un sistema iperbolico, il cui grado di dissipatività sia legato in un certo modo al grado di precisione, è sicuramente stabile in una vasta gamma di casi. Sebbene gli errori a lunghezze d'onda brevi siano smorzati, le grandezze veramente conservative non sono necessariamente perse. Le equazioni di Lax-Wendroff, che descriveremo nel È b, sono dissipative, ma massa, momento ed energia, in un certo senso, si conservano esattamente.

Nella maggior parte dei metodi espliciti a differenze per le equazioni (6) di Eulero, la condizione di stabilità risulta ancora essere la condizione di Courant: c Δt〈Δx, come per l'equazione delle onde, in cui c è la velocità locale (isoentropica) del suono. Questa condizione s'interpreta in modo semplice: le quantità fn_j⁺¹ (con f=u, ρ o ε) solitamente dipendono da fn_j+1, fn_j, fn_j-1, queste a loro volta da fn_j−₊¹₂, .., fn_j−_-¹₂ e così via, sicché la velocità massima con cui nel calcolo i segnali si possono propagare è Δx/Δt; non ci si può aspettare di ottenere risultati corretti a meno che Δx/Δt non sia grande almeno quanto la velocità c con cui i segnali (presenti nei dati iniziali) si possono propagare nella soluzione delle equazioni differenziali.

Gli schemi impliciti sono spesso incondizionatamente stabili (stabili per ogni valore di c Δt/Δx; in essi fn_j⁺¹ dipende da fn_j′, per ogni j′. Per molti problemi della fluidodinamica la stabilità incondizionata ha scarsa importanza, dato che generalmente, per motivi di precisione e risoluzione, cΔt deve essere dello stesso ordine di grandezza di Δx. Per altri problemi, in cui la velocità del suono varia molto da una regione all'altra o in cui, come in certi problemi meteorologici e astrofisici, il flusso consiste essenzialmente di una sequenza di stati di quasi equilibrio e non intervengono fenomeni acustici, conviene spesso lasciare che Δt sia considerevolmente più grande di Δx/c, almeno in certe regioni del sistema fisico.

Sistemi a differenze parziali, che richiedono un'alta precisione, per esempio un errore di troncamento dell'ordine O(Δt⁴), sono spesso scoraggianti nella pratica, al contrario dei metodi, come quello di Runge-Kutta per le equazioni differenziali ordinarie, che danno spesso grande precisione con poca fatica. Per un'equazione differenziale ordinaria, avente t come variabile indipendente, la conoscenza di un numero finito (e spesso molto piccolo) di grandezze a un istante t=t₀ è sufficiente (almeno in linea di principio) a determinare completamente ed esattamente la soluzione per ogni t>t₀; la precisione con cui poi si riesce a calcolare la soluzione per t=t₀+Δt dipende solo dall'abilità con cui si usano le informazioni disponibili. Per un'equazione a derivate parziali sarebbe necessario conoscere le funzioni all'istante t=t₀ per ogni valore delle variabili spaziali, non solo su un reticolo di punti, per determinare la soluzione a t>t₀. Pertanto, nel calcolare le soluzioni in t=t₀+Δt, non si è limitati solo da un'eventuale mancanza di abilità, ma anche dalla mancanza dei dati necessari. Non ha senso cercare metodi alla Runge-Kutta per le equazioni a derivate parziali, se i calcoli vengono effettuati su un reticolo spazio-temporale di punti.

b) Raccordo delle discontinuità agli urti; pseudoviscosità.

Nei primi calcoli di fluidodinamica macroscopica con urti (che riguardavano problemi con una sola variabile spaziale, x o r), vennero usati i cosiddetti metodi di raccordo agli urti; i metodi di pseudoviscosità vennero sviluppati in seguito. Descriveremo qui brevemente il metodo del raccordo agli urti.

La traiettoria di un'onda d'urto sia data da x=ξ(t); allora ξⁿ???36???ξ(tⁿ) è la posizione dell'urto all'istante tⁿ (in generale ξⁿ non coincide con una delle x_j; v. fig. 19). Le grandezze del flusso u, ρ, ε e p presentano discontinuità in x=ξ(t). Quindi, a ogni istante tⁿ, i valori limite u〈^±, ρ〈^±, ε〈^±, p〈^± da ciascuna parte del fronte d'urto, cioè in x=ξⁿ±0, sono considerati alla stregua di otto incognite ulteriori, da aggiungersi ai valori delle variabili di flusso nei punti regolari del reticolo x_j. Con la posizione ξⁿ e la velocità ξⁿ dell'urto, ci sono dieci nuove incognite. Esse sono sottoposte alle tre condizioni di discontinuità di Rankine-Hugoniot, all'equazione di stato da ciascuna parte dell'urto e a un'equazione ovvia del tipo

Come approssimazioni delle equazioni a derivate parziali con le differenze finite si scrivono quattro ulteriori equazioni, usando u〈^±, ρ〈^±, ecc., insieme ai valori sui punti limitrofi del reticolo (questo va fatto con notevole cura, per ottenere la stabilità). Il risultato consiste in un sistema di equazioni simultanee non lineari, che può essere risolto con un procedimento iterativo; esso determina il moto dell'urto e contemporaneamente permette al moto del fluido in ognuna delle due parti di influenzare il moto nell'altra parte attraverso le condizioni di discontinuità.

Per problemi con un'unica variabile spaziale in cui vi sia un unico urto forte, la cui posizione sia nota al tempo t=0, il metodo del raccordo delle discontinuità all'urto è molto adatto, in quanto dà una precisione e una risoluzione molto migliori dei metodi di pseudoviscosità.

La necessità di metodi di raccordo per i problemi multidimensionali è molto sentita per due motivi. In primo luogo, considerazioni di economia impongono in generale che il reticolo di punti sia molto più rado che nel caso dei problemi unidimensionali, così che, quando si usano metodi di pseudoviscosità, l'addolcimento degli urti e la conseguente perdita di risoluzione sono molto più gravi. Allo stesso tempo, le configurazioni dell'urto sono generalmente più complesse; quindi è necessaria una risoluzione maggiore, anziché minore, per descriverli accuratamente. Sono stati fatti numerosi tentativi di sviluppare metodi di raccordo in problemi a due dimensioni, ma appare chiaro che è ancora necessario altro lavoro. La posizione dell'urto al tempo tⁿ non può essere determinata da un singolo numero ξⁿ, ma dalle coordinate ξn_l, ηn_l, (l=1, 2, ...) di molti punti piuttosto ravvicinati sulla curva che descrive il fronte d'urto all'istante tⁿ. Le equazioni devono poi determinare l'evoluzione di questa curva nel tempo e insieme fornire la connessione tra i moti del fluido da ambedue le sue parti.

Il metodo della pseudoviscosità è stato sviluppato come semplice alternativa al metodo del raccordo da J. von Neumann e R.D. Richtmyer (v., 1950), sulla base di idee fisiche. Il lavoro di R. Becker e di altri aveva dimostrato che l'effetto della viscosità su di un urto è di sfumarlo in modo tale che la transizione dalla regione a bassa pressione a quella ad alta pressione è continua anziché discontinua. Se il coefficiente di viscosità è piccolo, lo strato di transizione è sottile e il resto del flusso è con buona approssimazione lo stesso che si ha nel caso di urti netti. L'idea fu quella di includere dei termini fittizi di viscosità nelle equazioni differenziali prima di trattarli col metodo delle differenze finite. In questo modo, tutti gli urti venivano trattati approssimativamente e automaticamente ogni volta che si presentavano. Con piccole modifiche di minore importanza, come l'uso di una viscosità quadratica anziché lineare, il metodo dette ottimi risultati nei problemi unidimensionali.

Come in seguito fu messo in evidenza da P. D. Lax, il metodo della pseudoviscosità contiene un'ipotesi nascosta, che spesso è stata ignorata nei lavori successivi. Per ottenere una soluzione precisa delle equazioni con la viscosità, è necessario che la spaziatura Δx dei punti del reticolo usato sia piccola rispetto a tutte le distanze entro cui le grandezze del flusso cambiano apprezzabilmente; in particolare, dovrebbe essere Δx≪d, indicando con d lo spessore dell'urto, invece che Δx≃d, come avviene di solito in pratica. Se un procedimento al limite, in cui Δx e d tendono simultaneamente a zero, anziché Δx per primo, dà almeno approssimativamente il risultato corretto, ciò dipende da caratteristiche delle equazioni a differenze finite che sono difficili da analizzare. In mancanza di un procedimento generale che fornisca un'analisi di questo tipo, von Neumann e Richtmyer sottoposero il particolare schema di differenze finite che stavano usando a numerose prove su configurazioni d'urto già note.

Un metodo migliore, proposto da Lax (v. Lax e Wendroff, 1960), è di usare equazioni a differenze che conservino massa, quantità di moto ed energia. Per evitare violente oscillazioni risonanti al seguito dell'urto, le equazioni dovrebbero essere, per quanto si conviene, dissipative (anche se non è necessario identificare quali particolari termini siano dovuti alla viscosità); le condizioni di discontinuità di Rankine-Hugoniot sono allora soddisfatte all'urto, perché queste condizioni sono basate sulle leggi di conservazione. Metodi che usano quest'idea sono stati formulati da Lax e Wendroff, da Godunov e da Rusanov.

Andrebbe fatto un breve accenno al problema dell'influenza dei bordi (esterni o interni) sulla stabilità degli schemi a differenze finite. In alcuni casi relativamente semplici questa può essere analizzata con i cosiddetti metodi energetici. Il primo tentativo di teoria più completa è stato fatto nel lavoro di Godunov e Rjabenkij (v., 1963). Essi fornirono un criterio di stabilità simile, nella sostanza, al criterio dato da von Neumann per la parte regolare del flusso. Algebricamente è molto più complicato del criterio di von Neumann, ma ciò nonostante può essere utile nel lavoro pratico, data la capacità dei moderni calcolatori di fare conti algebrici. Lavori recenti di B. Gustafson e H. O. Kreiss hanno dimostrato, tuttavia, che il criterio di Godunov-Rjabenkij può fallire in certi casi. Per concludere, è evidente che deve essere fatto ancora molto altro lavoro.

c) Metodi a differenze finite per l'equazione di Navier-Stokes.

La quantità e varietà dei metodi numerici usati per le equazioni di Navier-Stokes ne impediscono una discussione particolareggiata in questa breve rassegna. Discuteremo il caso del flusso viscoso incompressibile in due coordinate cartesiane spaziali x, y in funzione del tempo t, per illustrare alcuni nuovi problemi di calcolo che sorgono. Se u e v sono le componenti della velocità, ω è la vorticità e ψ è la corrente, le equazioni sono:

ω=−∆ψ, (151)

Dopo aver risolto approssimativamente la (150) col metodo delle differenze finite rispetto ai valori di ω all'istante tⁿ⁺¹ in tutti i punti dello spazio, diventa necessario risolvere l'equazione di Poisson (151) per la corrente ψ. Se le derivate della (151) vengono approssimate con formule di differenze finite (per esempio con la semplice espressione a cinque punti per il laplaciano), ne risulta un lungo sistema di equazioni, in cui sono implicati i valori di ψ al tempo tⁿ⁺¹ in tutti i punti dello spazio, contemporaneamente. Poiché vi sono due coordinate spaziali x e y, la matrice di questo sistema non è tridiagonale, ma ha elementi non nulli anche lontano dalla diagonale principale. Il sistema può essere risolto con un metodo di rilassamento (per es., il metodo implicito a direzione alternante, di Richtmyer e Morton), o con metodi diretti, che, tuttavia, sono molto più complicati del metodo corrispondente per un sistema tridiagonale. In questo caso, essendo la velocità del suono infinita, non c e un analogo diretto della condizione di Courant. In una regione in cui le componenti della velocità u e v non siano troppo grandi, la (150) ha le caratteristiche di un'equazione parabolica; se viene approssimata con una delle usuali equazioni esplicite a differenze finite e se, per semplicità, si pone Δx=Δy, la condizione di stabilità è νΔt〈ϑ(Δx)², dove ϑ è dell'ordine di ½ e dipende dal modo esatto di prendere le differenze.

Questa limitazione su Δt è spesso oltremodo grave. Per evitarla, dato che nel programma del calcolatore si trova già un algoritmo per risolvere equazioni del tipo di Poisson, spesso si rende implicita la (150), prendendo l'approssimazione per il laplaciano anche a tⁿ⁺¹.

In ogni caso, i termini di avvezione u(∂ω/∂x) e v(∂ω/∂y) devono essere trattati con precauzione. Se per questi termini si usano differenze centrate, ne risulta l'instabilità, per quanto piccolo possa essere Δt. Un rimedio che è stato usato spesso è di approssimare ∂ω/∂x con un quoziente di differenze in avanti o all'indietro, a seconda che u sia negativa o positiva, e analogamente per v(∂ω/∂y). Un metodo più preciso è di considerare l'intero primo membro della (150) come una differenziazione lungo la traiettoria della particella nello spazio x, y, t e di approssimarla con (ωn_j⁺_k¹−ῶⁿ)/Δtl, dove ῶⁿ si calcola seguendo la traiettoria (trattata come una retta) a ritroso dal punto (n_j⁺_, ¹_k) e approssimando t=tⁿ nel punto d'intersezione della traiettoria col piano t=tⁿ per interpolazione quadratica tra i valori di ωⁿ nei punti vicini dello spazio. La stabilità richiede allora che u Δt/Δx e v Δt/Δy non superino certi limiti dell'ordine di grandezza dell'unità, dipendenti dal particolare modo di prendere le differenze. La descrizione di un metodo analogo per il problema corrispondente del flusso stazionario si trova in Dennis (v., 1973).

d) Metodi con serie di potenze; il problema dell'urto staccato.

Adesso descriveremo un calcolo che si basa esclusivamente sull'analisi invece che sulle differenze finite. Davanti a un corpo arrotondato, a simmetria assiale, che si muova nell'aria con velocità supersonica, si trova generalmente il fronte di un'onda d'urto staccato, qual è mostrato in fig. 20 in un sistema di riferimento solidale con il corpo. Il flusso è subsonico vicino all'asse e supersonico più lontano, a valle. In condizioni normali, lo strato limite adiacente al corpo è di spessore trascurabile, così che si può supporre che il flusso sia ovunque non viscoso. Si noti, per inciso, che questo non implica un flusso derivante da potenziale, perché in generale la vorticità è non nulla dietro a un'onda d'urto incurvata.

Come in molti altri metodi adottati per affrontare questo problema, si assegna prima la superficie che rappresenta l'urto, quindi il calcolo fornisce le dimensioni e la forma che deve avere il corpo per produrre l'urto dato. Si suppongono dati i valori costanti della pressione, della densità e della velocità dell'aria davanti all'urto; i loro valori immediatamente dietro all'urto (i dati di Cauchy) derivano dalle condizioni di discontinuità di Rankine-Hugoniot. Se la superficie d'urto data e l'equazione di stato sono analitiche, i dati di Cauchy sono funzioni analitiche di un'opportuna coordinata lungo l'urto e possono essere sviluppati in serie di potenze di questa coordinata. Con un programma preliminare si calcolano i coefficienti di questi sviluppi in serie e col programma principale si calcolano i coefficienti rimanenti dello sviluppo completo nelle due variabili, trovando e usando relazioni di ricorrenza tra i coefficienti che si ottengono sostituendo gli sviluppi nelle equazioni differenziali. Con un programma finale si calcolano poi varie quantità sommando numericamente le serie nei punti desiderati del flusso.

La riuscita del metodo dipende dal teorema di CauchyKovalevskaja; bisogna quindi dimostrare che la superficie dell'urto non coincide in alcun punto con una superficie caratteristica. Il sistema di equazioni a derivate parziali dato sotto è del quarto ordine, quindi ci dobbiamo aspettare quattro famiglie di caratteristiche nel piano della fig. 20 (anche se alcune di esse coincidono e alcune potrebbero non essere reali). Un'analisi delle equazioni porta alle conclusioni seguenti: le traiettorie delle particelle o le linee di corrente sono sempre caratteristiche doppie; nella regione subsonica esse sono le sole caratteristiche reali. Nella regione supersonica ci sono altre due caratteristiche reali. Per ogni punto, esse sono l'inviluppo di una famiglia di onde sonore circolari prodotte da una rapida successione di piccole perturbazioni tutte partenti da quel punto, come è mostrato nella fig. 21. Dato che un urto è sempre subsonico rispetto al fluido che lo segue, una di queste caratteristiche - quella più vicina all'urto - raggiunge l'urto a una distanza finita a valle e attraversa la superficie dell'urto con un angolo non nullo. L'angolo aumenta man mano che ci si avvicina alla linea sonica. Le altre caratteristiche incontrano l'urto solo a monte e anch'esse con angoli diversi da zero; la stessa linea di corrente attraversa l'urto. Ne segue che una superficie d'urto non è in alcun punto una caratteristica.

La formulazione matematica del problema (v. Lewis, 1959; v. Richtmyer, 1960) è la seguente. La superficie dell'urto, in coordinate cilindriche r, z, sia data da

z=G(r)=G₀+G₂r²+G₄r⁴+... (153)

Siano u e v le componenti z e r della velocità, rispettivamente, e siano p, ρ, ε la pressione, la densità e l'energia interna specifica. Supponiamo che valga un'equazione di stato di gas ideale

Per z〈G(r) il flusso è uniforme

u=U (cost), v=0

e, con un'opportuna scelta delle unità, si può porre

p=p₀=1

ρ=ρ₀=1.

Davanti all'urto la velocità del suono è √-γ-p-₀-/-ρ-₀ = √-γ e il numero di Mach è M=U/√-γ.

Si definiscono delle coordinate curvilinee x, y dietro alla superficie d'urto (v. fig. 22) nel modo seguente:

x=z−G(r), y=r−r₀;

le relazioni inverse sono

r=r₀+y, z=x+G(r₀+y)=x+g(y).

L'urto si trova in x=0. Per le condizioni di discontinuità, è necessario introdurre l'angolo α tra la normale alla superficie d'urto e l'asse z, dato da:

Le condizioni di discontinuità di Rankine-Hugoniot all'urto si ottengono dalle (13-18); esse esprimono le leggi di massa, energia e quantità di moto. In esse p sta per p(0⁺, y) e analogamente per ρ, u e v; questi sono i dati di Cauchy sulla faccia posteriore della superficie d'urto. Le condizioni sono:

(componente normale della quantità di moto)

(componente parallela della quantità di moto).

Le equazioni a derivate parziali valide nella regione dietro all'urto sono

(componente z della quantità di moto)

(componente r della quantità di moto)

Formula

D/Dt denota l'operatore di differenziazione lungo le linee di corrente:

Formula

I termini in g′ compaiono per la non ortogonalità del sistema di coordinate.

Descriviamo ora brevemente il metodo della serie di potenze. Se f(x, y) sta per una delle funzioni p, ρ, u, v, o per qualsiasi grandezza intermedia che interviene nel calcolo, scriviamo

Formula

Se si risolvono le equazioni (154) rispetto a p, ρ, u, v (cioè rispetto a p(0⁺, y), ..., in cui le radici quadrate se ne vanno), le espressioni ottenute sono funzioni razionali di g′(y), ma g(y) si esprime mediante una serie di potenze in y (perché G(r) è espresso da una serie di potenze in r). I coefficienti delle serie per p(0⁺, y), ... cioè le quantità p_0k(k=0, 1, ...), ossono quindi essere determinati mediante calcolo diretto. Il problema consiste allora nel trovare

p_jk, ρ_jk, u_jk, v_jk(j+k≤K)

essendo note

p_0k, ρ_0k, u_0k, v_0k(k=0, 1, ..., K).

In vari tentativi di calcolo si è preso K uguale a 10, 14 e 19; il corrispondente numero di coefficienti per ogni funzione era ½(K+1)(K+2)=66, 120 e 210.

Le relazioni di ricorrenza per i coefficienti si ottengono, in linea di principio, sostituendo gli sviluppi in serie nelle equazioni differenziali (155) e uguagliando a zero in ogni equazione i coefficienti di x^jy^k, per ogni coppia d'indici (j, k). Si è invece costruito un algoritmo equivalente per ottenere i coefficienti p_jk, ... in modo induttivo. Per prima cosa si risolvono le equazioni differenziali (155) rispetto alle derivate in x:

Formula

dove i puntini stanno per funzioni razionali di p, ρ, u, v, ∂p/∂y, ∂ρ/∂y, ∂u/∂y, ∂v/∂y. Per ogni serie di potenze (156) l'insieme dei coefficienti

{f_jk:j+k≤K, j≤j′}

è detto ‛segmento K−j′' della serie. I segmenti K−0 di p, ρ, u e v costituiscono i coefficienti noti dei dati iniziali. Sono state sviluppate delle subroutines per lavorare sui segmenti operando sui coefficienti, in modo da poter effettuare addizioni, sottrazioni, moltiplicazioni, divisioni, differenziazioni e integrazioni sui polinomi rappresentati dai segmenti. Queste subroutines possono poi essere chiamate da singole istruzioni di un linguaggio di programmazione col quale il programmatore tratta direttamente le quantità che appaiono nelle (157). Il ciclo induttivo si svolge nel modo seguente: conosciuti i segmenti K−j′ di p, ρ, u, v, mediante la subroutine di differenziazione si ottengono i segmenti (K−1)−j′ di ∂p/∂y, ∂ρ/∂y, ∂u/∂y, ∂v/∂y (questo abbassa il grado rispetto alla y). Mediante questi, si calcolano i segmenti (K−1)−j′ dei secondi membri delle (157). Integrando questi ultimi rispetto a x, si ottengono i segmenti K−(j′+1) di p, ρ, u e v. Con ciò si completa un ciclo del calcolo. Dopo K cicli, partendo dai segmenti K−0 noti, si trovano tutti i coefficienti desiderati, con j+k≤K.

Con un'ulteriore applicazione della subroutine d'integrazione si ottiene anche la serie di potenze (o, meglio, i coefficienti fino ai termini di grado K) della corrente:

Formula

in cui è stato omesso un fattore 2π. I valori di ψ(x, y) nei vari punti del flusso si possono poi ottenere sommando la serie. Le linee di corrente ψ=cost servono a due scopi: 1) la linea di corrente ψ=0 dà la forma del corpo che produce il fronte d'urto assegnato (v. fig. 23); 2) una verifica della precisione è fornita dalla costanza dell'entropia lungo le linee di corrente.

Questo algoritmo è detto ‛metodo dei segmenti successivi'. Forse va messo in evidenza che, sebbene il metodo sia essenzialmente analitico, richiede tuttavia l'uso di un moderno calcolatore. Le relazioni di ricorrenza sono infatti troppo impegnative per essere trovate e usate a mano: la determinazione dei coefficienti delle serie di potenze per p, ρ, u e v si effettua con circa 10⁷ passaggi aritmetici, per valori di K compresi tra 10 e 20. Il metodo richiede anche l'uso di un'aritmetica significativa quale sarà descritta brevemente nel È f. Essendo questo metodo analitico, esso è in grado di fornire una precisione molto maggiore di quella dei metodi a differenze finite (stime della precisione mediante calcoli di controllo sono descritte in seguito). Inoltre, il metodo non è affetto dalle difficoltà delle condizioni di stabilità che sono inerenti a ogni procedimento a differenze finite che parta dall'urto. Queste difficoltà derivano dal fatto che il problema di Cauchy non è ben posto nella regione subsonica, dove le equazioni hanno il carattere di un sistema ellittico: la soluzione esiste (per dati di Cauchy analitici) ed è unica, ma, come nel corrispondente problema di Cauchy per l'equazione di Laplace, essa non dipende con continuità dai dati di Cauchy. Una perturbazione ‛infinitesima' della superficie d'urto provoca una grande perturbazione del flusso a piccole distanze a valle.

e) Serie di potenze; prolungamento analitico.

È noto che la regione di convergenza di una serie di potenze in due variabili complesse x e y è costituita dall'unione di bicilindri, cioè di regioni definite da relazioni del tipo ∣x∣〈R₁, ∣y∣〈R₂; quindi la regione di convergenza per x e y reali sarà una regione simmetrica del piano x, y è virtualmente impossibile determinare a priori questa regione in problemi come quello dell'urto staccato. I calcoli di prova hanno dimostrato chiaramente che questa regione non è abbastanza grande per comprendere qualsiasi parte della superficie del corpo, quale è determinata dalla linea di corrente biforcata ψ=0; nasce quindi la necessità di trovare un prolungamento analitico della soluzione. Sono necessarie più informazioni di quelle contenute nella serie di potenze troncata e sommata per j+k=K, che è polinomiale ed è quindi uguale alla propria continuazione analitica su tutto lo spazio complesso C². In un metodo, proposto da Lewis nel 1959, si sceglie una nuova curva C′, parallela al fronte d'urto, in x=x₀, con x₀ abbastanza piccolo perché la prima serie di potenze converga per x=x₀ e per y in un intorno di zero; si ripete l'intero calcolo, con le stesse equazioni a derivate parziali e con i dati di Cauchy ottenuti su C′ dal primo calcolo. Cioè si scrive:

Formula

in cui f sta per una qualunque delle funzioni p, ρ, u o v. I dati di Cauchy per il nuovo calcolo sono

Formula

dove gli ???19???_0k si ottengono dal primo calcolo mediante

Formula

Questo metodo si è rivelato molto accurato nella pratica.

Lewis ha dimostrato che, in condizioni ragionevoli, se si trascurano gli errori di arrotondamento, il metodo appena descritto dà una vera continuazione analitica della soluzione, per K→∞. Più in generale, egli ha dimostrato che questo è vero per una vasta classe di sistemi di equazioni differenziali, a condizione che il secondo sviluppo giunga al grado K′, eguale alla parte intera di sK, al tendere di K all'infinito, s essendo una costante fissata in (0, 1).

Ci sono tre tipi di controlli della precisione per il calcolo dell'urto staccato: 1) si possono confrontare in medesimi punti del flusso gli sviluppi effettuati attorno a due punti diversi dell'urto (due valori diversi di r₀); 2) su una linea di corrente la quantità di Bernoulli B=½(u²+v²)+γp/(γ−1)ρ è costante. Inoltre, poiché le condizioni di discontinuità di Rankine-Hugoniot ci dicono che B non cambia attraverso l'urto (e, d'altra parte, B è lo stesso su tutte le linee di corrente a monte dell'urto), B dovrebbe essere costante in ogni punto del flusso; 3) essendo l'entropia costante su una linea di corrente, dovremmo avere

Formula

dove p, ρ e p₁, ρ₁ si riferiscono a due punti posti sulla stessa linea di corrente, cioè a due punti in cui la corrente ψ data dalla (158) ha lo stesso valore.

Nel miglior calcolo di prova effettuato con doppia precisione su un IBM 704 per K=19, questi controlli hanno indicato che nell'intera regione del flusso si otteneva una precisione di otto cifre significative, compresa la regione subsonica sulla punta e la regione supersonica a grandissime distanze a valle. Per valori piccoli e medi di r₀ (distanza del polo dello sviluppo dall'asse), era necessario un solo prolungamento analitico per raggiungere il corpo; per valori più grandi di r₀ ne erano necessari due.

f) Aritmetica significativa.

Il primo calcolo di prova è stato effettuato con una precisione di nove cifre in aritmetica significativa (v. sotto, cap. 11), con K=14 e quindi con 120 termini in ogni serie di potenze. Si è trovato che molti dei coefficienti per i quali era j+k>9÷10 avevano perso ogni significato, per essersi forse annullati in qualcuno dei 10⁷ passaggi aritmetici presenti nell'algoritmo prima descritto. Quando le serie erano sommate senza tener conto del problema della significatività, si ottenevano risultati di scarso valore. La routine impiegata per sommare le serie di potenze fu allora modificata in modo tale da eliminare tutti i termini il cui indice di significatività fosse inferiore a un certo valore (corrispondente alla precisione di circa una cifra); in tale modo si ottennero risultati molto precisi, almeno per punti x, y posti ben all'interno della regione di convergenza della serie di potenze.

Per ‛aritmetica significativa' s'intende un metodo di calcolo in cui ogni numero non è semplicemente rappresentato da una frazione e da un esponente, come nel solito metodo della virgola mobile (floating point), ma in cui esiste anche qualche sistema per indicare quante delle cifre della frazione sono significative. Ricordiamo che ai tempi in cui si effettuavano i conti a mano si usava, scrivendo un dato o un risultato finale o intermedio, sottolineare l'ultima cifra significativa del numero. Così, quando occorreva effettuare un'operazione aritmetica tra due numeri, con semplici regole, si otteneva l'ultima cifra significativa del risultato da quelle degli operandi. Questi procedimenti erano considerati parte essenziale di una buona tecnica di calcolo. Ci sono metodi per ottenere lo stesso scopo nei moderni calcolatori, ma vengono usati raramente e questo all'autore sembra riprovevole, se si pensa a quante possibilità di annullamenti ci sono in lunghi calcoli numerici.

A volte, come in questo problema, tener conto della significatività delle cifre non solo serve a valutare la qualità dei risultati, ma anche a ottenere il risultato. E questo perché, se una grandezza perde di significato, può essere non solo imprecisa, ma anche di un ordine di grandezza completamente sbagliato. Per esempio, se si calcola e^-20, sommando la serie di potenze di e^-x con x=20, su una macchina a virgola mobile con 10 cifre (naturalmente è assurdo farlo sapendo cosa succede), il risultato non solo è sbagliato, ma è circa 100.000 volte più grande di quello esatto. Ogni qual volta si sommino serie semplici o multiple che rappresentino correzioni sempre più piccole di un risultato, è essenziale omettere i termini che abbiano perso significato.

In una forma di aritmetica significativa, ciascun numero è rappresentato da una frazione, da un esponente e da un indice di significatività tutti combinati in un'unica parola del calcolatore. L'indice di significatività è un numero intero (che potrebbe essere compreso tra 0 e 10 in un calcolatore decimale, tra 0 e 40 in uno binario), che dice quante cifre della frazione (la quale è sempre mantenuta normalizzata, come nel metodo usuale della virgola mobile) sono significative. L'indice di significatività di una somma, di una differenza, di un prodotto, o di un quoziente si ottiene dagli indici degli operandi con le stesse regole usate una volta nei calcoli a mano.

Nell'altra forma usuale di aritmetica significativa (v. Ashenhurst e Metropolis, 1959) non c'è un indice di significatività e le frazioni generalmente non sono normalizzate. Ogni frazione ha il numero esatto di zeri all'inizio, così che tutte le altre cifre, tranne un numero fisso di ‛cifre di sicurezza' all'estrema destra della frazione; sono significatitive. Il numero di zeri all'inizio di una somma, di una differenza, di un prodotto o di un quoziente è determinato da regole equivalenti a quelle accennate per il caso del calcolo a mano. Lo scopo delle cifre di sicurezza è quello di assorbire l'accumulo degli errori di arrotondamento e di impedire loro di contaminare le cifre veramente significative. (Questa, naturalmente, è una distinzione arbitraria, in quanto il calcolatore elettronico non ha modo di distinguere le cifre significative da quelle di sicurezza).

Entrambe le forme di aritmetica significativa sono state usate nel problema dell'urto staccato ed entrambe con risultati soddisfacenti.

11. Osservazioni conclusive; problemi per il futuro.

Sebbene i principî fondamentali che sono alla base della fluidodinamica del XX secolo fossero ben noti già nel 1900, alcune conseguenze di questi principi, scoperte dopo d'allora, sono sufficientemente rilevanti da poter essere considerate, a buon diritto, concetti nuovi e principî fondamentali. Tra questi il concetto di strato limite, i principi che sono alla base del distacco dello strato limite, vari principi e teoremi sulla teoria dell'ala portante, la teoria della stabilità dei flussi viscosi, la scia vorticosa di von Kàrmàn, la teoria statistica delle correlazioni e degli spettri di potenze (che è certamente importante, anche se la teoria statistica della turbolenza non è completa), gli aspetti analitici del flusso compressibile e i metodi di calcolo.

È molto probabile che lo sviluppo ulteriore riguarderà in gran parte i rapporti della fluidodinamica, come si è qui definita, con altri campi della fisica, quali l'elettromagnetismo, la teoria cinetica della materia, la cinetica chimica, la relatività, la teoria quantistica e la fisica nucleare.

Tuttavia, rimangono alcuni problemi importanti da risolvere anche nella fluidodinamica pura. Quello principale è il problema della turbolenza e della convezione turbolenta. Decenni di fallimenti dei tentativi di costruire una teoria statistica in analogia con quella dei gas suggeriscono che questa analogia sia sterile, forse perchè: a) non c'è un analogo delle equazioni hamiltoniane del moto e b) mentre le molecole di un gas (e anche di una miscela di gas) sono tutte molto piccole e di dimensioni quasi uguali, i vortici che trasportano quantità non trascurabili di energia nella turbolenza hanno dimensioni che variano per molti ordini di grandezza e in generale i più grandi non possono essere considerati piccoli da nessun punto di vista. Ciò nonostante, ci sono sistemi fisici in cui è presente la convezione (per esempio nelle stelle della sequenza principale e nelle variabili cefeidi) e il cui comportamento globale è prevedibile con grande precisione, cioè fenomenologicamente su tempi lunghi. Questo sembra un forte indizio del fatto che certi tipi di principi statistici siano applicabili in modo preciso.

Probabilmente un po' meno difficile è il problema della stabilità di un flusso laminare rispetto a perturbazioni di ampiezza finita; questa sembra essere la chiave per la comprensione dell'insorgere della turbolenza.

L'applicazione della moderna teoria dei sistemi dinamici a perturbazioni di ampiezza finita può essere feconda. Questo approccio è stato suggerito da Ruelle e Takens (v., 1971), come già si è detto nel cap. 6, È e, ma per ora è soltanto a uno stadio speculativo.

Molto difficile dal punto di vista matematico, anche se forse, in pratica, di minor importanza immediata, è la teoria matematica del problema a valori iniziali del flusso non viscoso in due o tre variabili spaziali.

A questi vorrei aggiungere il problema di trovare metodi di calcolo basati più sull'analisi e meno sulla forza bruta; credo che i metodi basati esclusivamente sulle differenze finite siano ormai stati sviluppati al limite delle possibilità e che, ciò nonostante, sotto molti aspetti lascino ancora parecchio a desiderare.

Bibliografia.

Ashenhurst, R. L, Metropolis, N. C., Unnormalized floating-point arithmetic, in ‟Journal of the Association for Computing Machinery", 1959, VI, pp. 415-428.

Bakhmeteff, B. A., The mechanics of turbulent flow, Princeton 1941.

Bergman, S., Application of integral operators to singular differential equations and to computation of compressible flows. MRC technical summary report, Madison 1966.

Bers, L., The expansion theorem for sigma-monogenic functions, in ‟American journal of mathematics", 1950, LXXII, pp. 705-723.

Bers, L., Mathematical aspects of subsonic and transonic gas dynamics, New York 1958.

Betchov, R., Criminale, W. O. Jr., Stability of parallel flows, New York 1967.

Birkhoff, G., Helmholtz and Taylor instability, in ‟Proceedings of Symposia in applied mathematics of the American Mathematical Society", 1962, XIII, pp. 55-76.

Blasius, H., Grenzschichten in Flüssigkeiten mit kleiner Reibung, in ‟Zeitschrift für Mathematik und Physik", 1908, LVI, pp. 1-37.

Bohr, H., Zur Theorie der fastperiodischen Funktionen, in ‟Acta mathematica", 1924, XLV, pp. 29-127.

Case, K. M., Stability of inviscid plane Couette flow, in ‟Physics of fluids", 1960, III, pp. 143-149.

Chandrasekhar, S., Hydrodynamic and hydromagnetic stability, New York 1961.

Courant, R., Friedrichs, K. O., Supersonic flow and shock waves, New York 1948.

Courant, R., Hilbert, D., Methods of mathematical physics, 2 voll., New York 1953-1962.

Curle, N., Davies, H. J., Modern fluid dynamics, London 1968.

Dennis, S. C. R., The numerical solution of the vorticity transport equation, in Proceedings of the third international conference on numerical methods in fluid mechanics (a cura di H. Cabannes e R. Témam), vol. II, Heidelberg 1973, pp. 120-129.

Fife, P., Considerations regarding the mathematical basis for Prandtl's boundary layer theory, in ‟Archive for rational mechanics and analysis", 1968, XXVIII, pp. 184-216.

Godunov, S. K., Rjabenskij, V. S., Spectral criteria of stability of boundary-value problems for non-self-adjoint difference equations, in ‟Uspekhi matematischeskikh nauk", 1963, XVIII, 3, pp. 3-14.

Goldstein, S., Modern development in fluid dynamics, New York 1965².

Hiemenz, K., Die Grenzschicht an einem in den gleichformigen Flüssigkeitsstrom eingetauchten geraden Kreiszylinder, Göttingen 1911.

Howarth, L., On the calculation of the steady flow in the boundary layer near the surface of a cylinder in a stream, Aeronautical research committee (Great Britain). Report and Memorandum 1632, 1935.

Howarth, L., On the solution of the laminar boundary layer equations, in ‟Proceedings of the Royal Society" (Series A), 1938, CLXIV, pp. 547 ss.

Howarth, L. (a cura di), Modern developments in fluid dynamics. High speed flow, Oxford 1953.

Kármán, T. von, The fundamentals of the statistical theory of turbulence, in ‟Journal of aerospace sciences", 1937, IV, pp. 131-138.

Kármán, T. von, Howarth, L., On the statistical theory of isotropic turbulence, in ‟Proceedings of the Royal Society" (Series A), 1938, CLXIV, pp. 192-215.

Kirchgässner, K., Kielhöfer, H., Stability and bifurcation in fluid dynamics, in ‟Rocky Mountain journal of mathematics", 1973, III, pp. 275-318.

Krzywoblocki, M. Z. von, Bergman's linear operator method in the theory of compressible fluid flow, New York 1960.

Ladyženskaja, O., The mathematical theory of viscous incompressible flow, New York 1963.

Lamb, H., Hydrodynamics, New York 1932⁴.

Landau, L. D, Lifshitz, E. M., Fluid mechanics, London 1959.

Lax, P. D., Hyperbolic systems of conservation laws and the mathematical theory of shock waves. S.I.A.M. series on applied mathematics, vol. XI, Philadelphia 1973.

Lax, P. D., Wendroff, B., Systems of conservation laws, in ‟Communications on pure and applied mathematics", 1960, XVII, pp. 381-399.

Lewis, G. E., Two methods using power series for solving analytic initial value problems, New York 1959.

Lin, C. C., The theory of hydrodynamic stability, London 1955.

Macphail, D. C., An experimental verification of the isotropy of turbulence produced by a grid, in ‟Journal of aerospace sciences", 1940, VIII, pp. 73-75.

Milne-Thompson, L. M., Theoretical aerodynamics, New York 1968⁵.

Mises, R. von, Schiffer, M., On Bergman's integration method in two-dimensional compressible flow, in Advances in applied mechanics (a cura di R. von Mises e T. von Kármán), vol. I, New York 1948, pp. 249-285.

Monin, A. S., Yaglom, A. M., Statistical fluid mechanics: mechanics of turbulence, Cambridge, Mass., 1971.

Morawetz, C. S., On the nonexistence of continuous transonic flows past profiles. I, in ‟Communications on pure and applied mathematics", 1956, IX, pp. 45-68.

Neumann, J. von, Richtmyer, R. D., A method for the numerical calculation of hydrodynamical shocks, in ‟Journal of applied physics", 1950, XXI, pp. 232-237.

Nikuradse, J., Laminare Reibungsschichten an der länsangeströmten Platte, Berlin 1942.

Olejnik, O. A., Mathematical problems of boundary layer theory, Minneapolis 1969.

Prandt, L., Über Flüssigkeitsbewegung bei sehr kleiner Reibung, in Proceedings of the third international mathematics congress, Heidelberg 1904.

Rayleigh, J. W. S., Theory of sound, New York 1945².

Richtmeyer, R. D., Power series solution, by machine, of a nonlinear problem in two dimensional fluid flow, in ‟Annals of the New York Academy of Sciences", 1960, LXXXVI, pp. 828-842.

Richtmyer, R. D., Morton, K. W., Difference methods for initial value problems, New York 1967.

Robertson, H. P., The invariant theory of isotropic turbulence, in ‟Proceedings of the Cambridge Philosophical Society. Mathematical and Physical Sciences", 1940, XXXVI, pp. 209-223.

Roždestvenskij, B. L., Discontinuous solutions of systems of quasilinear equations of hyperbolic type, in ‟Uspekhi matematischeskikh nauk", 1960, XV, 6, pp. 59-117.

Ruelle, D., Takens, F., On the nature of turbulence, in ‟Communications on mathematical physics", 1971, XX, pp. 167-192.

Schlichting, H., Boundary layer theory, New York 1960⁶.

Schwarzschild, M., Structure and evolution of the stars, Princeton 1958.

Spiegel, E. A., Convection in stars, in ‟Annual review of astronomy and astrophysics", 1971, IX, pp. 323-352.

Squire, H. B., On the stability of the three-dimensional disturbances of viscous flow between parallel walls, in ‟Proceedings of the Royal Society" (Series A), 1933, CXLII, pp. 621-628.

Stern, M., The rolling up of vortex sheet, in ‟Journal of applied mathematics and physics", 1956, VII, pp. 326-342.

Stewart, R. W., Triple velocity correlations in isotropic turbulence, in ‟Proceedings of the Cambridge Philosophical Society. Mathematical and physical sciences", 1951, XLVII, pp. 146-175.

Stewartson, K., The theory of laminar boundary layers in compressible fluids, Oxford 1964.

Taylor, G. I., Stability of a viscous liquid contained between two rotating cylinders, in ‟Philosophical transactions of the Royal Society" (Series A), 1923, CCXXIII, pp. 289-343.

Taylor, G. I., Statistical theory of turbulence, in ‟Proceedings of the Royal Society" (Series A), 1935, CLI, pp. 421-478; 1936, CLVI, pp. 307-317.

Uberoi, M. S., Corrsin, S., Diffusion of heat from a line source in isotropic turbulence. National Advisory Committee On Aeronautics, report n. 1142, Washington 1953.

Wiener, N., On the representation of functions by trigonometrical integrals, in ‟Matematische Zeitschrift", 1926, XXIV, pp. 575-616.