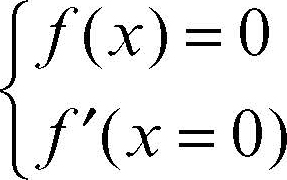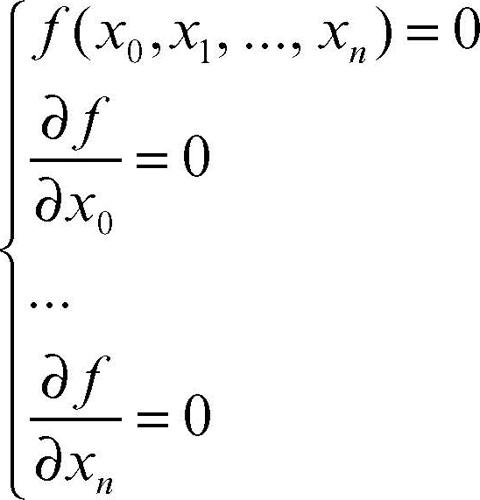discriminante

discriminante

discriminante in algebra, numero associato a un polinomio in una variabile in funzione dei suoi coefficienti reali, solitamente indicato con la lettera greca Δ (delta). Il suo annullarsi esprime una condizione necessaria e sufficiente affinché il polinomio abbia radici multiple. Il discriminante di un polinomio di secondo grado della forma ax ² + bx + c, con a, b, c reali, è

a seconda che esso sia positivo, nullo o negativo, il polinomio ha due radici reali distinte, due radici reali coincidenti (soluzione doppia) o due radici complesse coniugate (e quindi sono tali le soluzioni della corrispondente equazione di secondo grado). Il discriminante di un polinomio di terzo grado della forma ax ³ + bx ² + cx + d (che ha sempre almeno una radice reale) è:

Più in generale, il discriminante di un polinomio si annulla per gli stessi valori per cui si annulla il → risultante del polinomio e della sua derivata. Il discriminante di un’equazione algebrica ƒ(x) = 0 di grado n è una funzione razionale intera di ƒ(x) il cui annullarsi è condizione necessaria e sufficiente perché l’equazione stessa abbia una radice almeno doppia. Poiché una radice almeno doppia dell’equazione ƒ(x) = 0 è radice anche dell’equazione ƒ ′(x) = 0 e viceversa, ogni radice comune alle due equazioni ƒ(x) = 0 e ƒ ′(x) = 0 è almeno doppia per la prima equazione, il discriminante di ƒ(x) = 0 è, a meno di un fattore numerico, il risultante del sistema

Il discriminante di un’equazione algebrica omogenea ƒ(x₀, x₁, ..., x_n) = 0 è analogamente una funzione razionale intera dei coefficienti dell’equazione il cui annullarsi denota che nello spazio n-dimensionale l’ipersuperficie da essa definita possiede un punto almeno doppio. Il discriminante è perciò dato, a meno di un fattore numerico, dal risultante del sistema:

Un’espressione del discriminante di un polinomio come funzione dei suoi coefficienti è determinata per mezzo della matrice di → Sylvester associata.

□ Per il concetto di discriminante di una conica, si veda → conica.