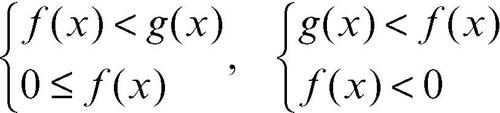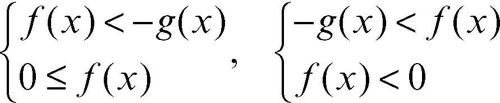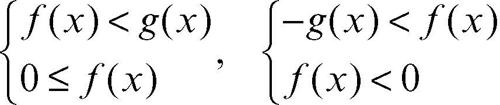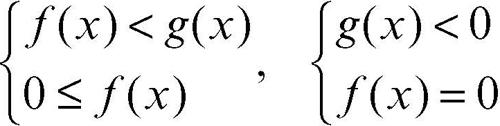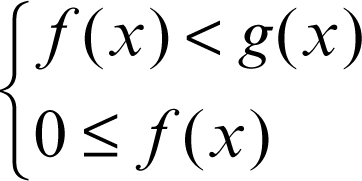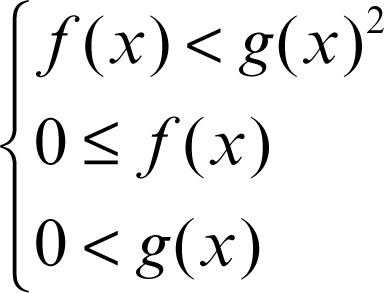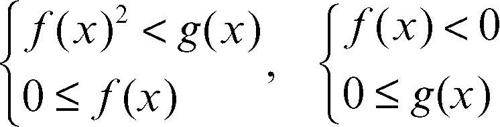disequazione

disequazione

disequazione in algebra, formula aperta, contenente cioè una o più variabili incognite, in cui compare uno dei predicati «minore» (<), «minore o uguale» (≤), «maggiore» (>) o «maggiore o uguale» (≥). Assegnata una disequazione in una incognita x, ƒ(x) < g(x), definita in un insieme A ⊆ R, risolvere la disequazione significa determinare l’insieme S degli x appartenenti ad A che soddisfano tale formula. L’insieme A è detto dominio della disequazione; l’insieme S è detto insieme delle soluzioni della disequazione e può eventualmente anche essere vuoto, nel qual caso la disequazione è detta impossibile. Se il problema è espresso tramite una disuguaglianza larga (≤ invece di <), allora, oltre alle soluzioni della disequazione ƒ(x) < g(x), l’insieme delle soluzioni S comprenderà anche le eventuali soluzioni dell’equazione ƒ(x) = g(x). Una disequazione si dice propria se non è né sempre verificata né mai verificata; in altre parole, una disequazione è propria se l’insieme S non è né vuoto né coincide con il dominio della disequazione. Per esempio, le disequazioni x ² ≥ 0 e x ² < 0 sono rispettivamente sempre vera e sempre falsa, dunque non sono proprie; la disequazione 0 < x è invece propria: essa è vera se x è positivo ed è falsa altrimenti. Una disequazione non propria è detta identica quando è verificata per un qualunque valore attribuito all’incognita. Una disequazione si dice algebrica se le variabili che compaiono nelle espressioni ƒ e g che la definiscono sono legate da operazioni algebriche; se le due espressioni ƒ e g sono polinomi, si definisce il grado della disequazione come il maggiore tra i loro rispettivi gradi. Una disequazione algebrica si dice frazionaria (o razionale) se le funzioni ƒ e g sono razionali, vale a dire se esse sono il rapporto di due polinomi; irrazionale se compaiono radici di espressioni contenenti l’incognita (vedi oltre). Si usa l’espressione disequazione ridotta a forma tipica per indicare una disequazione algebrica in cui una delle due espressioni che la definiscono (dette anche primo e secondo membro) è 0 e l’altra è un polinomio, il cui grado è il grado della disequazione.

Risolvere una disequazione significa determinare i valori dell’incognita (compresi generalmente in un intervallo o in più intervalli) che sostituiti a essa, trasformano la disequazione in un proposizione vera. Il problema può risultare difficile perché rimanda a quello della risoluzione della corrispondente equazione. Per esempio, nel caso di una disequazione algebrica di grado n in un’incognita, la sua risoluzione è sostanzialmente equivalente al problema di trovare tutte le radici di un polinomio ƒ(x) di grado n, e questo è un problema che in generale non è affatto banale, giacché per n > 4 non esiste una formula risolutiva esprimibile tramite radicali dell’equazione generale di grado n (→ Abel-Ruffini, teorema di). In alcuni casi tuttavia si può ridurre la difficoltà del problema usando raccoglimenti a fattor comune e abbassando quindi il grado dei singoli fattori nella disequazione.

L’insieme delle soluzioni di una disequazione algebrica della forma ƒ(x) > 0 può essere graficamente rappresentato come un’unione di un numero finito di intervalli connessi sulla retta reale. Se infatti ƒ(x) ha grado n e se x₁, …, x_m sono le sue radici (ordinate in ordine crescente e contate con la relativa molteplicità), allora la positività e la negatività di ƒ saranno costanti su ogni intervallo aperto della forma (x_i, x_i+1); dunque l’insieme delle soluzioni della disequazione considerata sarà l’unione dei siffatti intervalli su cui la disequazione stessa è verificata. Poiché il numero delle soluzioni di un’equazione algebrica non è mai maggiore del suo grado (per il teorema fondamentale dell’algebra), segue che tali intervalli sono al più in numero di n + 1. Nel caso in cui la disequazione considerata sia della forma ƒ(x) ≥ 0, allora l’insieme delle soluzioni sarà un’unione di intervalli chiusi: tali intervalli saranno gli stessi che compaiono nel caso precedente, cui però si aggiungono i punti estremali corrispondenti alle radici di ƒ(x).

Similmente al caso di un’incognita, si possono definire disequazioni in due incognite e più in generale con un arbitrario numero di incognite: se ƒ(x, y) e g(x, y) sono due funzioni di due variabili reali definite su uno stesso insieme A ⊆ R², allora il problema sarà di trovare le coppie (x, y) di numeri reali in A che soddisfano la disuguaglianza ƒ(x, y) < g(x, y). In modo del tutto analogo si tratta il caso di una disequazione in n incognite. Si estendono a questi casi tutte le definizioni date per il caso di un’incognita e restano validi i principi di equivalenza per le disequazioni: per esempio, ogni disequazione algebrica di primo grado in due incognite è riconducibile a una disequazione del tipo y > ax + b (rispettivamente y ≤ ax + b) oppure y < ax + b (rispettivamente y ≥ ax + b); pertanto il relativo insieme delle soluzioni sarà rappresentabile geometricamente come il semipiano aperto (rispettivamente chiuso) dei punti di R² posti al di sopra o al di sotto il grafico della retta di equazione y = ax + b.

Si parla di sistema di disequazioni quando si hanno due o più disequazioni che debbono essere tutte soddisfatte: l’insieme delle soluzioni, in tal caso, è dato dall’intersezione degli insiemi delle soluzioni delle singole disequazioni (→ sistema di disequazioni).

Risoluzione di una disequazione algebrica di primo grado in un’incognita su R

Per le proprietà dei numeri reali, si può supporre che la disequazione abbia una delle due seguenti forme:

con a diverso da zero. Sia S l’insieme delle soluzioni della disequazione. Si presentano allora due possibili casi:

• se a > 0, allora S coincide con l’intervallo aperto (−b/a, +∞) nel caso (1) e con l’intervallo chiuso [−b/a, +∞) nel caso (2);

• se a < 0, allora S coincide con l’intervallo aperto (−∞, −b/a) nel caso (1) e con l’intervallo chiuso (−∞, −b/a] nel caso (2).

Risoluzione di una disequazione algebrica di secondo grado in un’incognita su R

Si può supporre che la disequazione abbia una delle due seguenti forme:

con a diverso da zero. Sia Δ = b² − 4ac il discriminante del polinomio ƒ(x) = ax ² + bx + c. Si presentano allora vari possibili casi:

• a < 0 e Δ > 0: se x₀ e x₁ sono le radici distinte di ƒ(x), allora, supposto x₀ < x₁, l’insieme delle soluzioni coincide con l’intervallo aperto (x₀, x₁) nel caso (1) e con l’intervallo chiuso [x₀, x₁] nel caso (2);

• a > 0 e Δ > 0: se x₀ e x₁ sono le radici distinte di ƒ(x), allora, supposto x₀ < x₁ l’insieme delle soluzioni coincide con l’unione degli intervalli aperti (−∞, x₀) e (x₁, +∞) nel caso (1) e con l’unione degli intervalli (−∞, x₀] e [x₁, +∞) nel caso (2);

• a < 0 e Δ = 0: se x₀ è l’unica radice di ƒ(x), allora l’insieme delle soluzioni è vuoto nel caso (1) e coincide con l’insieme costituito dal solo x₀ nel caso (2);

• a > 0 e Δ = 0: se x₀ è l’unica radice di ƒ(x), allora l’insieme delle soluzioni è l’unione degli intervalli aperti (−∞, x₀) e (x₀, +∞) nel caso (1) e coincide con l’intero insieme dei numeri reali nel caso (2);

• a < 0 e Δ < 0: l’insieme delle soluzioni è vuoto tanto nel caso (1) quanto nel caso (2);

• a > 0 e Δ < 0: l’insieme delle soluzioni è tutto l’insieme dei numeri reali tanto nel caso (1) quanto nel caso (2).

Disequazioni con valore assoluto

Sono disequazioni in cui l’incognita compare all’interno di un’espressione scritta in valore assoluto. Ci si può talvolta ridurre a tre particolari situazioni notevoli:

a) |ƒ(x)| < |g(x)|: l’insieme delle soluzioni della disequazione è l’unione delle soluzioni dei sistemi

b) |ƒ(x)| < g(x): l’insieme delle soluzioni della disequazione è l’unione delle soluzioni dei sistemi

c) ƒ(x) < |g(x)|: l’insieme delle soluzioni della disequazione è l’unione delle soluzioni della disequazione ƒ(x) < 0 con le soluzioni dei sistemi

Disequazioni esponenziali

Disequazioni in cui una delle incognite compare nell’esponente di un’opportuna base. Per risolvere una disequazione esponenziale può risultare utile applicare la funzione logaritmo, che è monotòna crescente e pertanto trasforma l’equazione in una forma equivalente. Per esempio, la disequazione esponenziale a^x > b, dopo aver applicato ad ambo i membri la funzione logaritmo in base a, assume la forma equivalente x > log_a(b): dunque l’insieme delle soluzioni è l’intervallo aperto (log_a(b), +∞).

Disequazioni irrazionali

Disequazioni in cui una delle incognite compare nell’argomento di una radice. Per risolvere una disequazione irrazionale si ricorre, in modo opportuno, all’elevazione a potenza. Se l’indice n della radice sotto cui compare l’incognita è dispari, allora la funzione xⁿ è monotòna crescente e pertanto, elevando alla potenza n-esima ambo i membri della disequazione, si ottiene una disequazione equivalente. Ciò è falso se invece l’indice n è pari. In questo caso occorre prima di tutto imporre che il radicando sia positivo; dunque, ci si riconduce allo studio di un opportuno sistema di disequazioni. Nel caso quadratico, ci si può talvolta ricondurre a tre particolari situazioni, qui analizzate più in dettaglio. Un’analoga casistica sarà valida nel caso di radici con un arbitrario indice pari:

la disequazione è equivalente al sistema

la disequazione è equivalente al sistema

l’insieme delle soluzioni della disequazione è l’unione degli insiemi delle soluzioni dei due sistemi

Disequazioni logaritmiche

Disequazioni in cui una delle incognite compare nell’argomento o nella base di un logaritmo. Per risolvere una tale disequazione può risultare utile applicare la funzione esponenziale, che è monotòna crescente e pertanto trasforma l’equazione in una equivalente. Per esempio, la disequazione logaritmica log_a(x) > b, dopo aver applicato ad ambo i membri la funzione esponenziale in base a, assume la forma equivalente x > a^b: dunque l’insieme delle soluzioni è l’intervallo aperto (a^b, +∞).

Disequazioni goniometriche

Disequazioni in cui una delle incognite compare nell’argomento di una o più funzioni goniometriche. Nella risoluzione di una disequazione goniometrica, possono risultare utili le formule trigonometriche. Se le funzioni goniometriche che compaiono nella disequazione hanno tutte il medesimo argomento, il problema può essere semplificato utilizzando le formule parametriche: assumendo come nuova incognita, mediante una sostituzione, la tangente dell’argomento dimezzato, ci si riconduce infatti a una disequazione equivalente non goniometrica. Per esempio, la disequazione goniometrica sin(x) + cos(x) ≥ 1, dopo avere applicato le formule parametriche, assume la forma equivalente

Ponendo t = tan(x/2), la disequazione assume la forma equivalente t + 1 ≥ t ²+ 1, le cui soluzioni sono 0 ≤ t ≤ 1. Pertanto l’insieme delle soluzioni nell’incognita iniziale x è