disgiunzione
disgiunzione
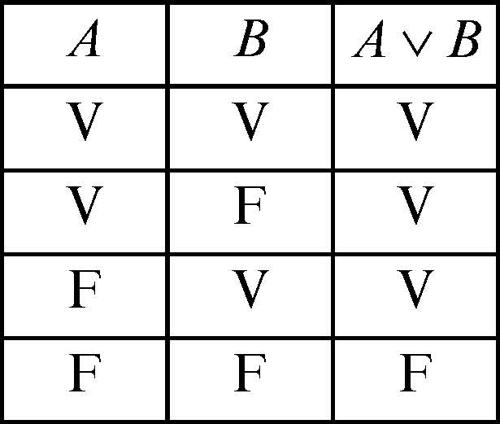
disgiunzione in logica, connettivo, indicato con il simbolo ∨, che corrisponde, nel linguaggio naturale, alla congiunzione disgiuntiva «o» usata in senso inclusivo (come il latino vel) e non esclusivo (come il latino aut). Si considerino per esempio gli enunciati: 1) P: «il numero n è pari»; 2) M: «il numero n è multiplo di 5». L’enunciato composto P ∨ M: «il numero n è pari o multiplo di 5» è vero per tutti i numeri pari (come 4) oppure multipli di 5 (come 15), così come per i numeri che siano sia pari sia multipli di 5 (come 10); per questo si parla di disgiunzione inclusiva. Dati due enunciati A e B, l’enunciato A ∨ B (si legge «A o B») è falso solo nel caso in cui sia A sia B siano falsi, mentre è vero in tutti gli altri casi, come espresso dalla seguente tavola di verità:
Attraverso la disgiunzione inclusiva o è possibile unire anche più di due proposizioni; per esempio si può connettere la proposizione A ∨ B a un’altra proposizione C formando la proposizione (A ∨ B) ∨ C. Tale proposizione è logicamente equivalente alla proposizione A ∨ (B ∨ C): per la disgiunzione vale, quindi, la proprietà associativa. Per estensione, la disgiunzione di un qualsiasi numero di enunciati è un enunciato falso se e solo se tutti gli enunciati che la compongono sono falsi. La disgiunzione fra due enunciati, in logica proposizionale, svolge un ruolo analogo a quello dell’unione fra due insiemi nella teoria degli insiemi: l’insieme di verità dell’enunciato A e l’insieme di verità dell’enunciato B, dove per insieme di verità di un enunciato si intende l’insieme di quegli elementi per cui l’enunciato è vero. Infatti, dati due insiemi A e B, un elemento appartiene all’unione A ∪ B dei due insiemi se e solo se appartiene ad almeno uno di essi. Ciò significa che un elemento non appartiene all’insieme A ∪ B se e solo se esso non appartiene né ad A né a B.
Disgiunzione generalizzata
Si parla di disgiunzione generalizzata quando il connettivo ∨ è applicato non solo a due proposizioni ma a un numero qualunque di proposizioni A1, A2, …, An. Si tratta di una generalizzazione del connettivo della disgiunzione, che può essere indicata con il simbolo
Una disgiunzione generalizzata è vera quando almeno uno degli enunciati che la compone è vero. La precedente scrittura equivale quindi a Ǝi ∈ {1, …, n}: Ai, ovvero: esiste un indice i per cui Ai è vera (→ quantificatore esistenziale). Le proprietà del quantificatore esistenziale (Ǝ) sono dunque strettamente connesse a quelle della disgiunzione generalizzata.
Disgiunzione esclusiva
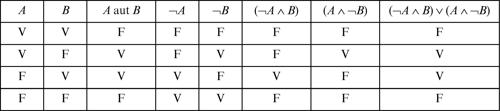
La disgiunzione esclusiva corrisponde, nel linguaggio naturale, alla congiunzione disgiuntiva «o» usata in senso esclusivo (come il latino aut). Può anch’essa essere considerata come un connettivo, ricavabile tuttavia dagli altri connettivi più usuali, compresa la disgiunzione inclusiva. Infatti, come nella lingua italiana la proposizione «mi scriverò a giurisprudenza o a matematica» è equivalente alla proposizione «mi iscriverò a giurisprudenza e non mi iscriverò a matematica o non mi iscriverò a giurisprudenza e mi iscriverò a matematica», così l’enunciato A aut B è logicamente equivalente a (¬A ∧ B) ∨ (A ∧ ¬B), come è evidente dalla tavola di verità, ed è vero soltanto nei casi in cui A e B hanno valori di verità differenti.