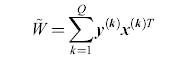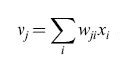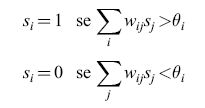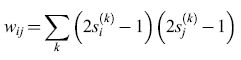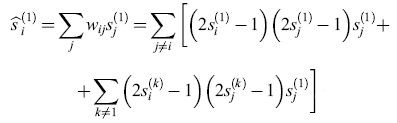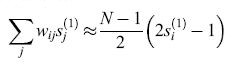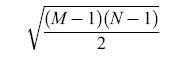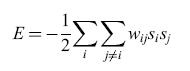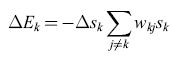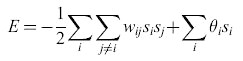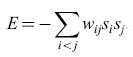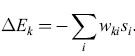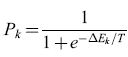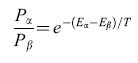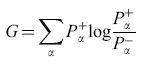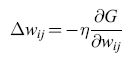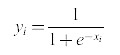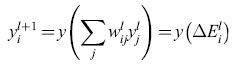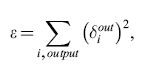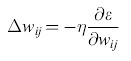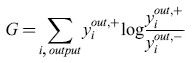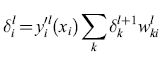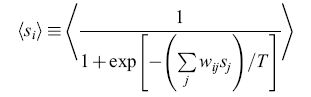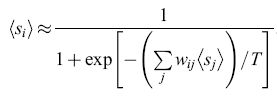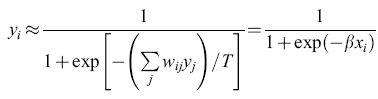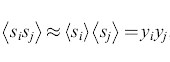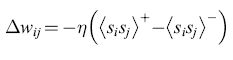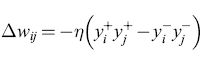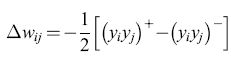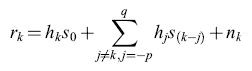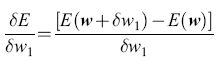Dispositivi neurali elettronici con funzioni specifiche

di Joshua Alspector - Frontiere della Vita (1999)

Joshua Alspector

(University of Colorado, Colorado Springs, Colorado, USA)

In questo saggio illustreremo le motivazioni che spingono a progettare dispositivi elettronici analogici o digitali con proprietà di reti neurali, e confronteremo le funzioni, le capacità e i consumi di energia di questi dispositivi con quelli dei sistemi biologici cui essi sono ispirati. Successivamente passeremo in rassegna una serie di esempi di realizzazioni elettroniche neurali, quali sensori, effettori, processori e sistemi con apprendimento. Per illustrare le ragioni delle scelte progettuali alla base della costruzione di un nostro sistema con apprendimento faremo una breve digressione storica sui modelli neuronali; quindi descriveremo gli elementi costitutivi dei sistemi neurali elettronici e cercheremo di delineare gli scenari futuri della ricerca su questi dispositivi.

Introduzione

Dal momento in cui il campo delle reti neurali artificiali ha ripreso vitalità, a metà degli anni Ottanta, sono stati varati numerosi progetti per la costruzione di sistemi neurali artificiali elettronici, di solito sotto forma di circuiti integrati. Di fatto la maggior parte di questi sistemi è stata realizzata tramite software su computer ad alta velocità. Attualmente è disponibile un numero considerevole di pacchetti software commerciali di questo tipo. Questi programmi funzionano su computer normalmente disponibili in commercio, hanno un'interfaccia grafica attraente, mostrano i risultati in modo grafico, includono molti algoritmi neurali differenti e hanno dimostrato il loro valore in applicazioni di interesse pratico.

Al contrario del successo riscosso dal software per reti neurali, le implementazioni di hardware neurale non hanno fatto registrare un successo commerciale. Gli sforzi più significativi, inclusi quelli delle maggiori società del settore, hanno permesso di raggiungere degli obiettivi tecnici ma non hanno portato a un successo di mercato. Sorge quindi il dubbio se valga la pena costruire questo tipo di dispositivi, visto che i computer tradizionali e il software sono già soddisfacenti. Per molti aspetti la costruzione di dispositivi neurali elettronici con funzioni specifiche è un atto di fede. Il progettista potrebbe sentirsi sfidato dall'enorme problema di 'costruire dei cervelli', emulare delle funzioni biologiche neuronali, o risolvere con questi strumenti un problema di interesse pratico.

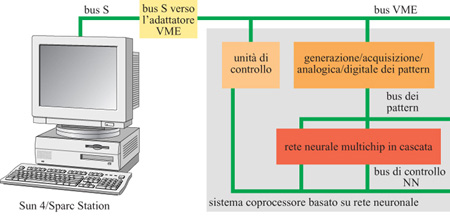
Se si considerano anzitutto le questioni di carattere pratico, si deve guardare al parallelismo intrinseco delle reti neurali come motivazione per costruire dei prototipi hardware. Le simulazioni di reti neurali su computer tradizionali richiedono tempi molto lunghi per l'addestramento della rete e per l'esecuzione delle sue funzioni. Costruendo dei sistemi neurali elettronici paralleli con hardware progettato specificamente si può sfruttare la naturale capacità di esecuzione in parallelo dell'elaborazione di tipo neurale. Ne è un esempio un processore per la selezione di eventi, utilizzato in esperimenti di fisica delle particelle di alta energia, basato su un chip appositamente prodotto.

Un'altra ragione che spinge verso la realizzazione hardware dell' elaborazione neurale è quella di creare un dispositivo compatto e a basso consumo, capace di svolgere una funzione specifica. Per esempio, se si volesse realizzare un sistema visivo con componenti che sono facilmente reperibili, sarebbe necessario mettere insieme una telecamera, un computer dotato di una certa quantità di memoria e opportuni dispositivi di input e output. Tutto ciò viene fatto frequentemente dai ricercatori che lavorano sulla visione, ma il risultato finale è un sistema ingombrante, con elevati consumi e, in definitiva, una soluzione poco elegante, se confrontata con la visione biologica, che invece è basata su organi di piccole dimensioni, a basso consumo e robusti. Sebbene non si possa ancora sperare di ottenere il livello di qualità degli organi biologici, è però possibile migliorare notevolmente la componentistica commerciale, creando un dispositivo con funzioni specifiche. l prezzi da pagare sono la mancanza di flessibilità e gli alti costi di sviluppo; questi ultimi potrebbero essere giustificati commercialmente solo per applicazioni di larga diffusione, per le quali possono essere ammortizzati con la vendita di un grosso numero di unità. Un esempio potrebbe essere la retina di silicio, capace di leggere i numeri degli assegni, di cui parleremo più avanti.

Un altro buon motivo per scegliere una realizzazione specifica si ha quando il valore di ogni pezzo è abbastanza elevato da giustificare uno sforzo progettuale speciale. Un esempio che richiede consumi ridotti, una dimensione limitata e ha un alto valore è quello del defibrillatore cardiaco intelligente, sviluppato presso l'università di Sidney (Coggins et al., 1995).

Confronto tra dispositivi analogici e digitali

Una decisione importante per chi realizza un dispositivo elettronico consiste nella scelta tra l'approccio analogico e quello digitale. Una soluzione generalmente conveniente consiste nello scegliere la migliore tecnica progettuale in base all'applicazione che si intende realizzare. Ognuna delle due tecniche ha i suoi vantaggi. Non è possibile rinunciare a una rappresentazione analogica se è necessario che il sistema interagisca, attivamente o passivamente, con il mondo reale. Per esempio, in un sistema per la visione la luminosità di un pixel viene in genere espressa con una quantità analogica. Potrebbe risultare vantaggioso convertirla in un formato digitale al livello del sensore del singolo pixel, ma questa soluzione comporterebbe l'elaborazione di una elevata quantità di dati digitali. La retina di silicio elaborata da C. Mead e collaboratori (Mead, 1989) effettua gran parte di questo processo di elaborazione in forma analogica direttamente sul chip, e in questo modo riduce la quantità di informazione che viene trasmessa allo stadio successivo di elaborazione. In un lavoro successivo degli stessi autori, l'informazione passata tra diversi chip prende la forma di una rappresentazione indirizzo-evento ed è digitale (Mahowald, 1994; v. anche il saggio di R. Douglas, M. Mahowald e A. Whatley, in questo volume). Più viene rinviata la conversione in digitale nel flusso di elaborazione, meno ne deve essere fatta. In generale il risultato complessivo sarà un sistema di ridotte dimensioni e bassi consumi, ma anche più specializzato e meno flessibile.

fig. 1

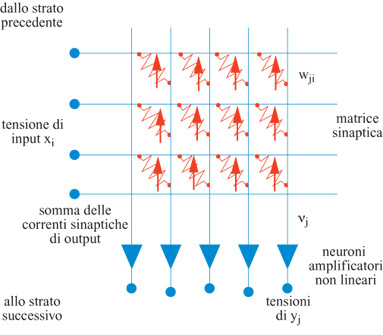
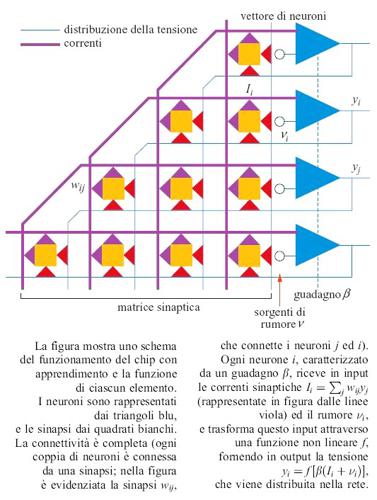
Le idee di base dell' elaborazione neurale in elettronica sono illustrate nella figura (fig. 1), che mostra la realizzazione di uno strato di pesi sinaptici. l pesi sinaptici Wji; vengono realizzati tramite resistori variabili. Lo strato elabora un vettore di input x per creare un vettore di output y. Se questa rete costituisse una memoria associativa, i pesi potrebbero essere memorizzati usando una regola di tipo hebbiano:

formula [1]

dove T indica l'operazione di trasposizione, W̃ è una matrice con elementi Wji; e le Q memorie vengono individuate dall'indice k: {x^(k), y^(k)} con k= l, ..., Q. Naturalmente sono possibili altri algoritmi di apprendimento per determinare i pesi sinaptici.

Si deve notare che i pesi non devono essere necessariamente dei veri e propri resistori. In genere, infatti, sono dei circuiti attivi, che producono delle correnti proporzionali al peso. Potrebbe anche darsi il caso che non vi sia necessità di un algoritmo di apprendimento, ma che i pesi siano fissati a priori per svolgere una funzione desiderata. Gli input di ogni strato (l' output dello strato precedente) sono delle tensioni. Dopo essere passate attraverso i resistori, le tensioni diventano correnti, che possono poi essere facilmente sommate lungo la linea di input ai neuroni. In definitiva l'input ai neuroni, v, è un vettore le cui componenti valgono:

formula. [2]

Questa costruzione analogica sfrutta la legge di Ohm per moltiplicare (i pesi sono semplicemente le conduttanze dei resistori) e le leggi di Kirchhoff per sommare (le correnti si sommano per il principio fisico della conservazione della carica). Questo tipo di costruzione analogica è estremamente compatto e permette di realizzare bassissimi consumi. Il passo successivo dell'elaborazione del segnale prevede l'immissione di questa somma di prodotti in un neurone non lineare, che in genere ha una funzione di attivazione data dalla tangente iperbolica di νj. È semplice ottenere questa funzione in hardware VLSI (Very Large Scale Integration, integrazione su grandissima scala) analogico utilizzando una coppia di transistor standard (Me ad, 1989). Bisogna poi fare in modo che l'input che giunge a questo amplificatore non lineare sia in corrente, mentre l'output deve essere in tensione, in modo da poter essere utilizzato dallo stadio successivo. È quindi piuttosto naturale pensare anche questo stadio in termini di elettronica analogica, perché questo permette di ottenere una realizzazione compatta e a bassi consumi.

fig. 2

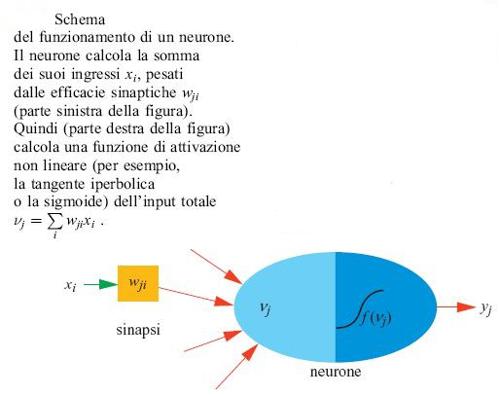
L'elaborazione del segnale richiesta dalla realizzazione elettronica è descritta nella figura (fig. 2). La figura è uno schema dell'elaborazione eseguita da ogni neurone. Si tratta della somma dei prodotti seguita dal calcolo di una funzione non lineare, svolta con molta eleganza da questo dispositivo analogico. Sfortunatamente, il prezzo da pagare per un dispositivo così compatto è la mancanza di precisione, di solito inferiore agli 8 bit, e di flessibilità (l'algoritmo o la funzione da svolgere sono fissati una volta per tutte).

Le realizzazioni di tipo digitale possono superare questi svantaggi, ma, di nuovo, ciò avviene pagando un certo prezzo. Con calcolatori digitali si possono ottenere dispositivi flessibili, ma lenti (perché l'elaborazione è seriale) e ingombranti (i calcolatori sono dispositivi di uso generale). In un dispositivo digitale con funzioni specifiche è possibile svolgere in parallelo il processo di elaborazione. Per esempio, gli elaboratori digitali di segnali (DSP, Digital Signal Processor) sono specializzati nel calcolo veloce di somme e prodotti, e la non linearità può essere ottenuta rapidamente utilizzando i valori della funzione precalcolati e tabulati (tabelle di ricerca). Tuttavia per ottenere l'elaborazione di un segnale non lineare ad alta precisione sono necessarie sequenze di calcoli veri e propri, anche solo per interpolare tra i valori della tabella di ricerca. Inoltre la realizzazione di lIn dispositivo digitale per la moltiplicazione veloce ad alta precisione richiede un grosso numero di transistor. Quindi un dispositivo digitale può avere alta precisione e flessibilità, ma solo a scapito della dimensione su chip e, di conseguenza, dei consumi. Un altro svantaggio delle tecniche digitali è la mancanza di una soluzione elegante per risolvere il problema della connessione con il mondo reale, che comunica con segnali analogici. A un certo stadio nella sequenza di elaborazione del segnale deve essere effettuata la conversione analogico-digitale.

Confronto con la biologia

Considerazioni energetiche

Energia dissipata nel cervello. - Il modello biologico per l'elaborazione neurale del segnale è costituito dal cervello e dai suoi sistemi di connessione, che attraverso il sistema nervoso arrivano agli organi sensoriali e ai muscoli. Il cervello ha una massa di circa 1,5 kg e dissipa intorno a 10 W di potenza. Se confrontato con i dispositivi elettronici di pari capacità di elaborazione, il cervello è incredibilmente compatto ed efficiente in termini di consumi. Per giungere a una stima di questa capacità, notiamo che il cervello contiene circa 10¹¹ neuroni, ognuno con circa 10³ sinapsi, per un totale di 10¹⁴ sinapsi o connessioni. Questo numero può essere visto come una misura della capacità di memoria del cervello, del tutto analoga al numero di byte della memoria di un computer. Il neurone biologico è un dispositivo piuttosto lento, che opera a frequenze dell' ordine di 100 Hz, un milione di volte più lento dei transistor. Tuttavia quando questa velocità viene moltiplicata per il numero di connessioni del cervello, si ottiene una potenza pari a 10¹⁶ connessioni elaborate al secondo (CPS, Connection evaluations Per Second).

Se si divide la dissipazione di potenza di 10 J/s per il numero potenziale di connessioni al secondo, si ottiene 10-¹⁵ J/connessione come costo energetico di una operazione di somma e moltiplicazione, supponendo tutte le sinapsi attive. È peraltro improbabile che si verifichi l'eventualità che tutte le sinapsi siano attive, e dunque la stima può essere considerata come l'energia consumata da una sinapsi a riposo. Per stimare l'energia necessaria a prendere una decisione neuronale, potremmo forse usare la stima di John von Neumann, che prevede 300 pJ per ogni azione binaria (decisione di un singolo neurone) del cervello. Assumendo che vi siano 3000 sinapsi per ogni neurone attivo si ottiene un valore di 10-¹³ J/connessione come costo energetico per l'elaborazione di una singola sinapsi attiva, circa 100 volte di più che nel caso del calcolo effettuato partendo dal consumo dell'intero cervello. Ciò implica che in ogni istante solo l' l % del cervello è attivo. Queste stime devono essere viste come qualcosa di speculativo e da usare solo per confronti grossolani.

Se si guarda ai dispositivi di base, i neuroni e le sinapsi, si vedono alcune differenze sostanziali rispetto ai dispositivi elettronici come i transistor. Il neurone è noto per essere rumoroso e impreciso: commuta dallo stato di non emissione a quello di emissione a massima frequenza quando il potenziale di membrana subisce una depolarizzazione inferiore a 50 mV. L'energia termica degli elettroni o degli ioni per unità di carica è kT / q (k è la costante di Boltzmann, T è la temperatura assoluta, q è la carica dell'elettrone), che a temperatura ambiente corrisponde a 25 mV. Questo significa che il neurone lavora a un rapporto segnale/rumore piuttosto basso, dal momento che la tensione di commutazione del neurone è solo 2kT / q. Se i transistor operassero a una tensione così bassa, commuterebbero di continuo in maniera incontrollata. Ciò che ci induce a pensare che i neuroni siano robusti rispetto al rumore termico è che vi sono diverse migliaia di porte elettro chimiche per ogni neurone. Ognuna in effetti è rumorosa, ma quando vengono mediate, grazie alla legge dei grandi numeri, rendono predicibili le modalità con cui avvengono le commutazioni.

Al contrario, l'elettronica dei semiconduttori forza le cariche a fluire in un singolo canale, e non può sfruttare la statistica allo stesso modo. Il silicio, semiconduttore molto diffuso, ha una differenza di energia tra la banda di valenza e la banda di conduzione di 1,12 V, molto al di sopra del rumore termico a temperatura ambiente, il che lo rende un commutatore molto affidabile. Se esistesse un semiconduttore con una differenza di energia di soli 50 m V, i transistor dovrebbero essere impiegati a temperature criogeniche per essere affidabili. Tuttavia tali circuiti sarebbero molto efficienti in termini di consumi, dal momento che l'energia dissipata nei circuiti tipici varia come il quadrato della tensione di alimentazione.

La progettazione delle sinapsi elettroniche. - Consideriamo ora l'energia richiesta per una connessione neurale elettronica che utilizzi l'elettronica attualmente disponibile. Per fare un confronto con l'elettronica analogica, abbiamo bisogno di definire un modello di sinapsi. Assumiamo che una cella di memoria dinamica ad accesso casuale (dRAM, dynamic Random Access Memory), che coinvolge la tecnologia più evoluta, sia un buon candidato. L'ipotetica sinapsi utilizzerebbe la carica depositata sul condensatore per rappresentare il valore del peso della sinapsi. Aumentando o diminuendo la carica, la sinapsi potrebbe cambiare il proprio peso sulla base di un algoritmo di apprendimento. Sebbene le dRAM oggi disponibili possano immagazzinare solo l bit di informazione, vi sono progetti di dispositivi che immagazzinano 2 bit o più (Murotani et al., 1997). Questo ci fa pensare che sarà possibile immagazzinare circa 8 bit di informazione per ogni condensatore, ovvero 256 valori, corrispondenti a 256 diverse quantità di carica. Questa precisione è confrontabile con quella dell'elettronica analogica usata in altre aree, come quella dei convertitori analogicodigitali.

I tipici processi in cui si usa una dRAM immagazzinano la carica in maniera molto efficiente, e richiedono solo una piccola quantità di energia per ripristinare (refresh) la carica su ogni condensatore. Questa energia di mantenimento è pari a circa 10-¹⁸ J/bit, e va confrontata con la stima di 10-¹⁵ J/connessione per il cervello a riposo. In una RAM statica o non volatile l'energia per il mantenimento dello stato di memoria è ancora più piccola (vicina a zero). Tuttavia durante la lettura e la scrittura della RAM l'energia è molto più elevata, circa 10-⁹ J/bit di energia 'attiva'. Questa quantità va paragonata alla stima di 10-¹³ J/connessione delle sinapsi attive. La maggior parte dell'energia spesa nel leggere o scrivere sulla RAM viene dissipata nella carica e scarica dei condensatori. La vera quantità di energia depositata nel condensatore della cella in una dRAM è solamente di 5.10-¹⁴ J/bit. Se questo condensatore potesse essere letto e scritto 'localmente' si potrebbe avere un costo di energia molto piccolo, dal momento che verrebbero ridotte le grosse capacità sono necessarie per un'architettura ad accesso casuale sulle linee di bit o di parole di bit. Sarebbe anche necessaria una quantità minore di carica sul condensatore della cella per renderlo leggibile, dato che verrebbe mantenuto il rapporto con la capacità della linea di lettura, che è più piccola. È ragionevole pensare che con le future tecnologie che lavorano a bassa tensione si potrà immagazzinare un'energia di cella di circa 10-¹⁵ J/bit, che corrisponde approssimativamente a depositare 6000 elettroni su di un condensatore ai cui capi vi è una differenza di potenziale di 1 V. Forse sarà possibile leggere queste celle localmente con amplificatori che permettono di avere una risoluzione di 8 bit (le differenze tra un valore e il successivo sarebbero dunque di soli 25 elettroni!). Tuttavia, in un dispositivo analogico reale che realizza una rete neurale, in cui bisogna pilotare da 100 a 1000 elementi per ogni neurone (elevato fan-out), si dovrà probabilmente aumentare la capacità totale (e quindi l'energia) di circa un fattore 100, per fare sì che l'amplificatore del neurone possa apprezzare le differenze tra valori vicini di efficacie sinaptiche che hanno una risoluzione di 8 bit (differenze di 2500 elettroni). Il risultato di ciò è una sinapsi con circa 10-¹³ J/connessione di energia 'attiva', almeno finché l'operazione di lettura/scrittura rimane locale rispetto ai neuroni a cui la sinapsi è connessa. Questa energia è la stessa energia 'attiva' di un 'neurone pensante' che abbiamo stimato in precedenza e va confrontata con i 10-⁹ J/bit di energia attiva in una dRAM: la necessità di un accesso casuale e remoto piuttosto che un accesso locale produce il fattore 10.000 di differenza tra i due. L'energia extra si può vedere come una conseguenza della necessità di comunicare su grosse distanze (carica e scarica dei condensatori relativi alle linee su cui viaggiano i bit o le parole di bit).

Queste considerazioni ci inducono a pensare che le regole di apprendimento locali (dove la sinapsi prende e rimanda informazione sul suo peso comunicando coi soli neuroni vicini) siano essenziali dal punto di vista dell'efficienza dei consumi, altrimenti il cervello dissiperebbe 100.000 W invece di 10 W, e sarebbe necessario un meccanismo di raffreddamento molto efficiente. Sulla questione dell'apprendimento locale torneremo ancora in seguito.

Questioni relative al sistema

Dimensioni. - Oltre alla notevole efficienza energetica dei sistemi neuronali biologici, ci si deve meravigliare anche della loro compattezza. Una sinapsi biologica è una struttura elettro chimica tridimensionale con dimensioni caratteristiche dell'ordine di 1 μm. Sebbene anche la cella dRAM abbia dimensioni di circa 1 μm, è essenzialmente una struttura bidimensionale che si posa sulla superficie di una piastrina di silicio molto più spessa, e quindi un numero equivalente di questo tipo di celle richiederebbe molto più spazio che nel caso biologico. Le caratteristiche cruciali sarebbero allora lo spessore della piastrina di silicio, la connessione delle celle e, tornando al problema dell'energia, il loro raffreddamento.

Il sistema di connessione. - La questione della connessione tra neuroni è una di quelle che probabilmente pongono dei limiti alla biologia. Nel cervello tali connessioni sono dirette e punto-punto: ne risulta che l'80% della rete neuronale è costituito da materia bianca (connessioni), e solo la parte restante da materia grigia (deputata all'elaborazione del segnale). Tuttavia, il cervello è ben lontano dall'essere completamente connesso, considerato che ognuno dei 10¹¹ neuroni è connesso solamente ad altri 1000 (un fattore 10⁸ in meno rispetto alla connettività completa). Vi saranno certamente delle valide ragioni computazionali e strutturali che giustificano una connessione se letti va, ma anche lo spazio sembra essere uno dei fattori limitanti.

Probabilmente il tipo di dispositivo in elettronica analogica che abbiamo discusso funziona al meglio anche con connessioni dirette. Tuttavia, come vedremo, l'estesa area richiesta per le connessioni su chip rappresenta uno svantaggio. Le tecniche digitali hanno certamente un vantaggio dal punto di vista connettivo, dal momento che il multiplex nel tempo dei segnali digitali è una tecnica robusta e ben sviluppata. Questa tecnica sfrutta la velocità dei circuiti elettronici, che è di gran lunga superiore a quella biologica. l transistor possono lavorare a frequenze che sono un milione di volte superiori ai 100 Hz dei neuroni biologici, e le connessioni metalliche su chip possono tollerare queste velocità. Sembra quindi naturale condividere la larghezza di banda su un singolo filo, e utilizzare le tecniche di multiplex per trasportare insieme diversi segnali neurali. Questa è una delle motivazioni alla base della rappresentazione indirizzoevento per la comunicazione tra chip neurali analogici. L'elettronica digitale può essere più veloce dell'elettronica analogica anche perché i tempi di reazione degli amplificatori analogici sono di gran lunga più lenti (di circa un fattore 1000) rispetto ai tempi di commutazione digitali.

Accoppiamento con l'ambiente. - Un'altra questione relativa al sistema, simile alla comunicazione con la memoria, è l'accoppiamento dei sensori e delle unità che operano sull'ambiente esterno (attuatori o effettori) con gli elaboratori dei sistemi neurali. Questo accoppiamento è molto stretto in biologia: per esempio, la retina effettua una quantità notevole di elaborazione prima di passare il segnale al nervo ottico, e possono esservi anche solo poche sinapsi tra un sensore tattile e un riflesso motorio. Al contrario, il sistema visivo digitale che è stato discusso in precedenza, costituito da componenti disponibili in commercio, mantiene sensori e processori a una certa distanza, il che porta a un elevato tempo di latenza e a risultati catastrofici in caso di errori di elaborazione.

l sistemi analogici possono avere, in linea di principio, accoppiamenti più stretti tra sensori e effettori, perché non vi è alcuna necessità di una fase di conversione dei dati, dal momento che i segnali dell'ambiente sono già in partenza analogici. La connessione diretta favorisce ritardi brevi, ridondanza e una degradazione moderata delle prestazioni in caso di errore. Tuttavia i sistemi analogici soffrono di ben noti problemi di imprecisione che provocano traslazioni dei livelli di correnti e tensioni, cui si può rimediare solo con continue ricalibrazioni. Ciò comporta che l'apprendimento e l'adattabilità siano parti importanti di un sistema analogico robusto. Qualora venga richiesta un'elaborazione parallela del segnale senza preoccuparsi dei vincoli sui consumi e sullo spazio, una realizzazione digitale è una scommessa più sicura dal punto di vista della tecnologia attuale. D'altra parte, se i consumi e lo spazio sono fattori importanti, allora un sistema adattivo analogico costituisce probabilmente la scelta migliore.

l sistemi neurali elettronici comprendono chip sensoriali come le retine e le coclee di silicio, chip per la classificazione in grado di svolgere funzioni di elaborazione specializzate, e chip con apprendimento per l'adattamento alle condizioni ambientali. Passeremo in rassegna alcuni esempi di ognuno di questi tipi di componenti dei sistemi neurali trattando le loro realizzazioni analogiche.

Alcuni esempi di realizzazioni analogiche

Chip sensoriali: le retine

Gli esempi migliori di sensori intelligenti, di tipo neurale e ispirati alla biologia, vengono dal lavoro di C. Mead e collaboratori (Mead, 1989). Una descrizione esaustiva di tutti i chip e i sistemi che sono stati progettati andrebbe oltre le intenzioni di questo saggio; tenteremo perciò di descrivere alcuni principi di base, e illustreremo i vantaggi che derivano dal prestare attenzione al modo in cui funzionano i sistemi biologici.

Utilizzando i principi biologici dell'elaborazione retinica si possono ottenere molti vantaggi rispetto ai sistemi di visione standard (Boahen, 1996), basati sulle telecamere con dispositivi ad accoppiamento di carica (CCD, Charge Coupled Device). Per esempio, un pixel CCD integra la luce, e quindi va in saturazione per elevati livelli di intensità luminosa. l chip CCD richiedono un segnale di reset dopo una lettura distruttiva dell'immagine campionata. l rivelatori elettronici di tipo neurale utilizzano fotodiodi come pixel sensori di luminosità. Questi rivelatori campionano continuamente il segnale luminoso, senza bisogno di una cadenza imposta da un clock, e possono lavorare in un intervallo dinamico molto esteso perché non integrano il segnale. L'assenza di una fase di reset permette anche di risparmiare energia. Il prezzo da pagare per tutto questo è il rumore dovuto alle inevitabili traslazioni di livello delle tensioni. La risposta di tipo neurale a questo problema è l'adattamento del guadagno e dei livelli di tensione per ridurre il rumore.

Le telecamere o le macchine fotografiche CCD utilizzano il controllo automatico di guadagno (AGC, Automatic Gain Control) per adattarsi all'intensità luminosa, tuttavia questo controllo va a influenzare allo stesso modo l'intero chip. Se l'illuminazione non è uniforme, come quando si vede una scena di un interno comprendente una finestra che dà su un esterno molto luminoso, allora il sistema fallisce nel conciliare la debole luce dell'interno con la luce chiara dell'esterno. Gli occhi e i chip retinomorfi usano un AGC locale, al livello del singolo pixel, che permette di percepire i dettagli sia dell'interno, sia dell'esterno, senza scurire le sezioni luminose e schiarire quelle scure. Ciò consente di estendere enormemente l'intervallo dinamico del chip, fino a eguagliare quello del singolo fotodiodo, che può arrivare a 10⁶, di molto superiore a quello di un dispositivo CCD, che è dell' ordine di qualche centinaio.

Le telecamere CCD standard trasmettono ogni dettaglio dell'immagine, un pixel alla volta e un'intensità alla volta. Molta di questa informazione è ridondante, dal momento che vi sono diverse aree piuttosto ampie che hanno più o meno la stessa intensità luminosa, e dal momento che queste aree non cambiano molto nel tempo. D'altra parte, le retine di silicio ignorano quasi completamente le aree che non cambiano nello spazio e nel tempo e trasmettono soprattutto l'informazione spazio-temporale nuova dell'immagine, riducendo così notevolmente l'informazione trasmessa allo stadio di elaborazione successivo. Questo costituisce un passaggio chiave dell'elaborazione del segnale visivo nel caso di rivelazione e analisi del moto. Una ulteriore riduzione della larghezza di banda necessaria a trasmettere informazione allo stadio di elaborazione successivo si ottiene poi adattando la discretizzazione del tempo alla velocità di cambiamento del segnale di input, e la discretizzazione delle ampiezze all'intervallo di ampiezze presenti nel segnale. Al contrario, i convertitori analogico-digitale standard devono tenere conto dell'intero intervallo di valori possibili, anche se i cambiamenti nel segnale sono rari.

Si può diminuire ulteriormente la larghezza di banda richiesta per passare informazione allo stadio di elaborazione successivo usando il protocollo di comunicazione indirizzoevento, che prende in prestito dalla biologia il principio di riportare solo i cambiamenti e l'informazione nuova. Sebbene la biologia non usi il multiplex di diversi segnali sullo stesso 'filo', la larghezza di banda più estesa dell' elettronica può essere meglio sfruttata usando il multiplex, anche se non nella maniera tradizionale, nella quale ogni sorgente di dati viene interrogata ciclicamente per una frazione di tempo prefissata. Al contrario, ogni chip mette dei dati sul filo quando c'è qualcosa degno di nota da riportare insieme al codice che identifica il mittente. Questo carico ulteriore viene facilmente compensato da un utilizzo più efficiente della larghezza di banda nel caso in cui l'informazione nuova sia relativamente rara. Questo protocollo richiede dei meccanismi che possano allo care dinamicamente la capacità del canale e arbitrare in caso di contesa per l'accesso allo stesso canale.

l principi sopra descritti per l'elaborazione retinica e dell'informazione sono sorprendentemente diversi da quelli previsti dall' approccio standard dell' elaborazione delle immagini, che fa uso di hardware e software disponibili in commercio. La rivelazione del segnale luminoso è continua e non campionata, il controllo del guadagno è locale e non globale, i segnali spazio-temporali sono passati in un filtro passa-banda per limitare l'informazione trasmessa a quella relativa ai cambiamenti, e il tempo e l'ampiezza sono discretizzati in modo adattivo, per rivelare l'informazione più rilevante presente nel segnale. Si possono ottenere ulteriori riduzioni della larghezza di banda del segnale trasmesso allo stadio di elaborazione successivo utilizzando il multiplex solo quando avviene un evento degno di essere riportato.

Un esempio commerciale. - Come esempio illustrativo di un'applicazione commerciale di elaborazione retinica e neurale presentiamo un chip per il riconoscimento di caratteri (OCR, Optical Character Recognition). Il problema da risolvere è quello di riconoscere i numeri stampati sugli assegni bancari, in modo che un terminale di un punto vendita possa addebitare l'importo dell'assegno sul conto corrente del cliente. Il problema del riconoscimento è relativamente semplice, grazie all'uso deliberato di un unico tipo di caratteri per l'inchiostro magnetico degli assegni bancari. In questo caso le ragioni principali per usare un dispositivo basato su un chip analogico sono i bassi costi, le piccole dimensioni e i bassi consumi. Funzionerebbe anche un dispositivo costituito da un chip CCD, un chip di interfaccia e un chip con un microprocessore, ma tale sistema sarebbe più ingombrante, più costoso e a consumo più elevato. Il problema è stato risolto integrando in un chip una retina di silicio, una rete neurale a pesi fissi e una parte di elaborazione digitale che serve a generare un output numerico da trasmettere al calcolatore, che addebita l'importo sul conto corrente.

La combinazione di retina e classificatore neurale ha 17.000 pesi precablati, è stata progettata in tecnologia CMOS (Complementary Metal Oxide Semiconductor, transistor del tipo metallo-ossido-semiconduttore complementare) a 1,6 μm, occupa 5 mmx5 mm di silicio e dissipa pochi milliwatt di potenza. Nonostante le piccole dimensioni del sistema, il dispositivo può leggere 20.000 caratteri al secondo, il che permette all'utente di passare l'assegno molto velocemente, pur mantenendo una buona affidabilità nel riconoscimento. Un chip così piccolo è anche molto economico da produrre. Il chip è stato un successo tecnico, ma per ragioni commerciali non è stato prodotto in serie in grandi quantità. Tuttavia fornisce un esempio di possibile uso futuro di chip dedicati ad applicazioni specifiche, di piccole dimensioni e di larga diffusione. Si possono immaginare chip per la lettura delle targhe dei veicoli, per la misura del flusso particolato, per l'ispezione di prodotti e per altri usi che richiedono sistemi visivi di dimensioni ridotte, economici e robusti.

Un esempio di controllo di un dispositivo che agisce sull'ambiente

Un esempio di applicazione dell'elaborazione di tipo neurale, caratterizzato da un alto valore più che da una larga diffusione, è fornito dal lavoro, svolto presso l'università di Sidney (Coggins et al., 1995), sui classificatori di piccole dimensioni e a basso consumo usati nei defibrillatori impiantabili per la cardioversione (lCD, lmplantable Cardioverter Defibrillator). L'lCD ha una funzione simile al pacemaker, ma è più sofisticato, poiché individua i battiti cardiaci irregolari e applica una stimolazione elettrica al cuore per mezzo di impulsi del defibrillatore che arrivano fino a 600 V. l consumi, l'affidabilità e le dimensioni sono caratteristiche importanti per questo tipo di dispositivi. Attualmente le loro capacità di elaborazione del segnale per individuare le aritrnie del cuore sono piuttosto ridotte. Di conseguenza alcune strutture temporali irregolari presenti nei battiti non vengono rivelate. L'obiettivo primario di questo progetto è di creare un classificatore più sofisticato ma a basso consumo, che possa analizzare l' elettrocardiogramma intracardiaco (lCEG, IntraCardiac ElectroGram) e decidere con maggiore precisione quando inviare gli impulsi del defibrillatore.

Il gruppo dell'università di Sidney ha sviluppato un classificatore neurale realizzato con circuiti analogici in grado di ottenere prestazioni notevoli (più del 90% delle risposte sono corrette) per aritmie che attualmente non sono trattabili con gli lCD. Il dispositivo consuma circa 200 nW e occupa un'area di circa 5 mm². Siccome il chip è analogico ed effettua una classificazione, è necessaria una fase di preaddestramento, in cui esso viene inserito in un circuito, e i parametri in ingresso vengono cambiati iterativamente fino a quando non vengono eliminate le traslazioni di livello e le imprecisioni. L'addestramento viene eseguito usando una tecnica di apprendimento perturbativa, che sarà discussa più tardi.

Chip analogici per l'elaborazione in parallelo

ETANN. - È stato messo sul mercato un interessante chip che contiene una rete neurale ad alta densità, denominato ETANN (Electrically Trainable Analog Neural Network, rete neurale analogica addestrabile elettronicamente; Holler et al., 1989). L'architettura generale è simile alla griglia di resistori illustrata nella figura l, ma le sinapsi sono più sofisticate. Nel caso più semplice, 64 input analogici sono completamente connessi a 64 amplificatori neurali attraverso una matrice di 64 x 64=4096 sinapsi. L' output dei 64 neuroni può essere usato direttamente o può essere inviato a un'altra matrice di 4096 sinapsi, attraverso la quale il segnale viene nuovamente sottoposto ai 64 input. Si ottengono così architetture con connessioni ricorrenti, sul tipo di quella del modello di Hopfield, che discuteremo nel seguito. Questa matrice sinaptica aggiuntiva può anche essere usata per altri 64 input (per un totale di 128) che si vanno a connettere ai 64 neuroni di output. Ogni neurone ha un proprio insieme di sinapsi di bias, che servono per fissare la soglia. Il totale di circa 10.000 sinapsi in grado di lavorare in parallelo garantisce prestazioni di 2 miliardi di operazioni di moltiplicazione-somma (connessioni) al secondo.

fig. 3

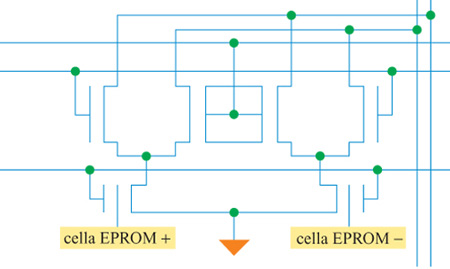
La caratteristica unica di questo chip è la sua capacità di operare interamente in analogico, anche nella memorizzazione dei pesi sinaptici. Ciò viene ottenuto usando dei dispositivi afloating gate con memoria di sola lettura cancellabile e programmabile elettricamente (EEPROM, Electrically Erasable Programmable Read-Only Memory). La cella sinaptica è mostrata in figura (fig. 3). La sinapsi calcola il prodotto tra una tensione analogica di ingresso e il peso sinaptico, memorizzato tramite un moltiplicatore di Gilbert. Il peso sinaptico viene memorizzato come carica suifloating gate delle due celle EEPROM. L'uso di due celle per l'operazione differenziale compensa molte delle traslazioni dei livelli di tensione e delle imprecisioni cui questo tipo di circuiti è soggetto, e permette anche ai pesi di cambiare in entrambe le direzioni. Il peso sinaptico è proporzionale alla differenza tra le tensioni di soglia delle due celle. Per aumentare un peso sinaptico si deve aggiungere carica a una delle celle, mentre per diminuirlo si deve aggiungere carica all'altra cella. La somma in corrente dell' output delle sinapsi completa l'operazione di moltiplicazione-somma. Queste correnti sono poi iniettate negli amplificatori dei neuroni di output, che calcolano una funzione non lineare di tipo sigmoide con guadagno variabile.

L'operazione di aggiornamento del peso sinaptico può essere effettuata solo su una sinapsi alla volta, a causa del metodo di selezione delle celle e delle tensioni, relativamente elevate, che sono richieste. Pertanto questa tecnica è adatta all'elaborazione parallela, una volta che il sistema è stato addestrato, ma non va bene per l'apprendimento parallelo. Tuttavia, a causa della natura analogica dell'elaborazione, intrinsecamente imprecisa, è comunque obbligatorio passare per una fase di preaddestramento, in cui il chip viene programmato per una certa funzione neurale. l pesi potrebbero essere regolati senza inserire il chip nel circuito di preaddestramento utilizzando delle simulazioni al computer, tuttavia l'imprecisione porterebbe a risultati in output diversi da quelli aspettati. Se invece si prende l'insieme di dati usati per l'addestramento, si inserisce il chip nel circuito di preaddestramento e si cambia un peso alla volta per regolare la funzione di trasferimento, in tal caso si può ottenere la relazione input-output desiderata. La modalità di funzionamento analogica e parallela permette di ottenere l'elaborazione di un numero di connessioni al secondo piuttosto elevato, se confrontato con quello dei processori di segnale digitali.

Dispositivi digitali

Le reti neurali digitali, in generale, non si ispirano al modello biologico per i sensori, gli elaboratori di informazione e gli attuatori. Di solito esse vengono progettate per rendere più veloce l'operazione di moltiplicazione-somma effettuando molte di queste operazioni in parallelo; ciò può essere ottenuto con sistemi di chip standard. Si possono, per esempio, combinare diversi DSP o microcontrollori per costruire una macchina con un certo grado di parallelismo. Tuttavia qui tratteremo solo chip con funzioni specifiche altamente paralleli, e costruiti appositamente per l'elaborazione neurale del segnale, riducendo l'insieme di istruzioni, i registri di memoria e il flusso dati a quanto è strettamente necessario per realizzare un algoritrno neurale particolare. In alcuni casi viene realizzato un solo algoritmo specifico, e questa mancanza di flessibilità viene compensata dall'alta densità di elementi di elaborazione sul chip. Talvolta si può risparmiare sullo spazio occupato su chip e sui consumi riducendo la precisione rispetto ai DSP o ai microcontrollori, che usano calcoli a virgola mobile con numeri a 32 bit. Vengono comunemente usate architetture che prevedono solo calcoli a virgola fissa a 8 o 16 bit per risparmiare spazio. Un esempio di sistema a 5 bit per reti del tipo afunzioni di base radiali (RBF, Radiai Basis Function) è il chip Ni1000 (Holler et al., 1992).

Il sistema CNAPS

Un esempio di dispositivo neurale digitale è il sistema CNAPS (Hammerstrom, 1991). Si tratta di un sistema con molti processori che esegue la stessa istruzione su ogni processore, ma su dati diversi, detto SIMD (Single Instruction Multiple Data, singola istruzione, dati diversi). Il sistema, costruito attorno al chip Inova N64000, contiene 80 elementi di elaborazione su di un chip di circa 2,5 cm². Solo 64 elementi vengono utilizzati, mentre i restanti 16 forniscono la ridondanza necessaria a compensare gli errori di produzione. Su ogni chip vi sono 13 milioni di transistor. Ogni elemento è in grado di effettuare una moltiplicazione a virgola fissa tra un numero a 9 bit e uno a 16 bit, e un'operazione di somma a 32 bit. Inoltre è dotato, localmente, di 4 kbyte di memoria statica ad accesso casuale, che servono per memorizzare i pesi. L'utente può scegliere tra pesi a 1,8 o 16 bit, a seconda delle necessità. Tutti i 64 elementi eseguono la stessa istruzione in parallelo. Si possono mettere in cascata vari chip estendendo i bus comuni. L'architettura di trasmissione sul bus (l'informazione viene trasportata a ogni elemento) permette di avere una rete di connessione ridotta al minimo, e ciò costituisce un grosso vantaggio nella progettazione digitale.

Ogni neurone viene assegnato a un elemento diverso, fino a quando non ve ne sono più di disponibili. Per reti più grandi bisogna assegnare più di un neurone a ogni elemento. Le prestazioni sono di 10 miliardi di CPS e 2 miliardi di aggiornamenti al secondo di tutte le connessioni (CUPS, Connection Updates Per Second). Questa architettura comincia ad avere problemi se sono necessari più di 4 kbyte, per ogni elemento, per la memoria dei pesi. Tuttavia è un'architettura flessibile e programmabile e può simulare la dinamica di diversi modelli, come la retropropagazione (backpropagation) e le mappe di caratteristiche autoorganizzanti (self-organizing feature maps).

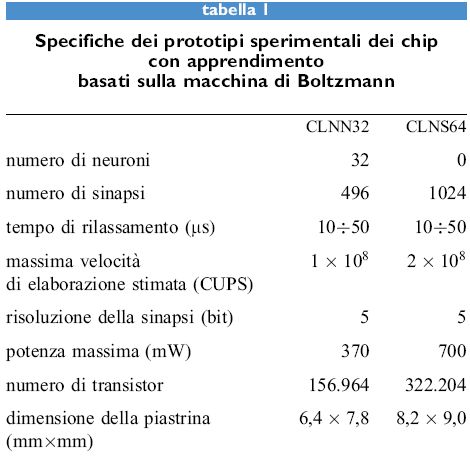
Un chip con apprendimento basato sulla macchina di Boltzmann

In questo paragrafo descriveremo il nostro lavoro fmalizzato alla realizzazione di un sistema elettronico con apprendimento, e i motivi alla base delle diverse scelte progettuali.

Cenni storici

L'attività recente sui modelli neuronali trova le sue radici in un articolo di W.S. McCulloch e W.H. Pitts (1943). In questo lavoro il cervello viene descritto come un insieme di neuroni a due stati: Si = 0 (corrispondente a un neurone quiescente) e Si = 1 (corrispondente a un neurone che emette impulsi alla massima frequenza). Se esiste una connessione tra il neurone j e il neurone i, denoteremo con wij la sua intensità. Ogni neurone aggiorna il suo stato in modo asincrono secondo la regola di soglia:

formula [3]

in cui θi è la soglia per l'emissione dell'impulso da parte del neurone i.

Il perceptron (Rosenblatt, 1961) si basa su un modello di questo tipo: si tratta di una macchina con struttura parallela in grado di imparare una regola a partire da esempi. La macchina consiste di un insieme di input, connessi tramite fili a un insieme di rivelatori di caratteristiche, il cui output può essere una funzione arbitraria degli input. Questi sono a loro volta collegati, attraverso uno strato di connessioni di intensità o pesi modificabili, a unità logiche a soglia, ognuna delle quali decide se un particolare pattern di input sia presente o meno, utilizzando la regola di soglia espressa dall'equazione [3]. È possibile realizzare elettronicamente le due componenti di questo dispositivo. L'unità logica a soglia può essere realizzata mediante un circuito bistabile, come un trigger di Schmitt (in cui si ha un cambiamento di stato logico se si raggiunge una certa soglia) oppure mediante un amplificatore operazionale, nel quale la funzione a soglia si può ottenere con un guadagno non lineare molto alto. I pesi modificabili si possono realizzare mediante resistenze variabili. Negli anni Sessanta venne effettivamente costruito un dispositivo di questo tipo (Widrow e Hoff, 1960): il suo nome era ADALINE (ADAptive LINear Element, elemento lineare adattivo). Il perceptron e l'ADALINE, come vedremo, sono alla base anche del nostro sistema VLSI.

Esiste un algoritmo, la procedura di convergenza del perceptron, che regola i pesi modificabili tra gli analizzatori di caratteristiche e le unità decisionali. Tale procedura è in grado di determinare con certezza una soluzione a un problema di classificazione di pattern, ove esista, sfruttando solo la possibilità di modificare l'insieme dei pesi. Sfortunatamente, come fu messo in luce da M. Minskye S. Papert (1969), vi è un'ampia categoria di problemi che i perceptron non sono in grado di risolvere, e cioè i problemi in cui sono coinvolti predicati di ordine maggiore di 1. L'operazione logica XOR, per esempio, è di ordine 2. Inoltre, la procedura di convergenza del perceptron non si applica a reti con più di uno strato di pesi modificabili tra input e output, poiché in questo caso non c'è modo di decidere quali pesi modificare quando si commette un errore. Questo problema di attribuzione dei meriti (credit assignment) ha rappresentato per lungo tempo un grosso ostacolo, superato solo grazie ai notevoli progressi nello sviluppo di algoritmi di apprendimento in reti a più strati.

Un'altra idea feconda, nell'ambito dei modelli di attività cerebrale, fu la proposta di D.O. Hebb (1949) sull'apprendimento neuronale. L'idea fondamentale è che, se un neurone risulta ripetutamente attivo in concomitanza con un altro, la sinapsi che li connette subisce modificazioni tali da aumentare l'efficienza di emissione di impulsi da parte dei neuroni considerati. Questo postulato sul ruolo correlazionale delle sinapsi è divenuto, sotto varie forme, il fondamento dei modelli di memoria associativa distribuita (Anderson et al., 1977; Kohonen, 1977). Mediante approcci simili si è affrontato anche l'apprendimento di pattern (Grossberg, 1969).

Nell'ambito di questi modelli si sono utilizzate diverse funzioni di trasferimento neurali. Il neurone binario di McCulloch e Pitts è rappresentato da una funzione gradino in corrispondenza della soglia; nel modello lineare la funzione è semplicemente proporzionale alla somma degli input. Un neurone reale è caratterizzato da una saturazione della frequenza di emissione di impulsi e da una soglia, con un comportamento approssimativamente lineare nella regione intermedia, e la sua funzione di trasferimento si rappresenta spesso mediante una sigmoide (Grossberg, 1973; Sejnowski, 1981). Tutte le funzioni di trasferimento esaminate si possono riprodurre bene attraverso un dispositivo elettronico. Un amplificatore operazionale possiede una funzione di trasferimento simile a una sigmoide; mediante un controllo di guadagno e una retro azione appropriati può riprodurre una funzione a gradino o, al contrario, funzionare in regime lineare. Nello sviluppo del nostro modello elettronico utilizzeremo questa proprietà.

Il modello di Hopfield di memoria associativa

Immagazzinamento di informazione. - La recente attività nella modellistica delle reti neurali è stata in gran parte stimolata da un modello non lineare di memoria associativa, dovuto a Il Hopfield (1982). I neuroni, in questo modello, sono di tipo binario, con una soglia che si ipotizza uguale a zero. Le informazioni (i 'ricordi'), costituite da vettori binari s^(k) = (s₁^(k), ... ,s_N^(k)) e contraddistinte dall'indice k, vengono memorizzate attraverso la somma sugli stati

formula [4]

in cui si usa il termine (2s - 1) per trasformare gli stati (0, 1) in stati (-1,1). Per un particolare ricordo ŝ⁽¹⁾ si ha:

formula [5]

Il primo termine nella somma ha valor medio (N -1)/2 per i termini j sommati su N neuroni, mentre il secondo termine in parentesi ha valor medio nullo, per ricordi casuali (e perciò pseudoortogonali), quando si somma in k su tutti gli M ricordi. Dunque:

formula [6]

Poiché questa quantità è positiva (maggiore della soglia θi = 0) se si⁽¹⁾ = 1, e negativa se si⁽¹⁾ = 0, la regola di soglia non modifica tale stato, che risulta stabile, a parte il rumore statistico proveniente dagli altri stati (k ≠ l), che ha varianza

formula [7]

fig. 4

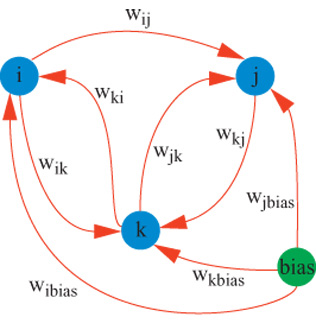
Il caso simmetrico e la misura dell'energia. - La rete proposta (fig. 4) è completamente connessa e simmetrica. In altri termini, per ogni coppia di neuroni contraddistinti dagli indici i e j, wij=wji, mentre Wu = 0. Utilizzando un'analogia, tratta dalla fisica, con il modello di Ising per i vetri di spin (Kirkpatrick e Sherrington, 1978), si può definire un'energia

formula [8]

Se un neurone Sk cambia stato, la variazione di energia corrispondente è

formula [9]

Per la regola di soglia, questa variazione può aver luogo solo se il segno della somma è lo stesso di ∆s_k.

Tutte le transizioni permesse fanno perciò diminuire l'energia, e si ha automaticamente una discesa di gradiente, finché non si raggiunge un minimo locale. Questa misura basata sull'energia fornisce un esempio di una funzione di Ljapunov globale, stabile sotto certe condizioni, che è una caratteristica tipica di una particolare categoria di sistemi (Cohen e Grossberg, 1983). Gli stati corrispondenti ai minimi rappresentano i ricordi del sistema. Si tratta di un sistema dinamico che, nel processo di rilassamento all'equilibrio, effettua un'elaborazione collettiva.

Il modello di Hopfield stimolò la costruzione di circuiti integrati capaci di realizzare questo tipo di memoria associativa (Sivilotti et al., 1985; Graf et al., 1986). Un sistema con N neuroni possiede circa N /logN stati stabili, e può memorizzare circa 0,14N stimoli prima che i termini di rumore provochino degli errori (v. il saggio di J. Cowan, Storia dei concetti e delle tecniche nella ricerca sulle reti neurali). Inoltre, quando il sistema si trova vicino al suo limite di capacità di memoria si presentano molti stati spuri, che rappresentano dei falsi ricordi. La ricerca di minimi locali richiede che i ricordi siano tra loro scorrelati, ma d'altra parte le correlazioni, e le generalizzazioni che ne derivano, formano l'essenza dell'apprendimento. Una macchina veramente capace di apprendimento, che rappresenta il nostro obiettivo, deve stabilire queste correlazioni creando delle rappresentazioni interne e cercando i minimi globali, ovvero risolvendo un problema di soddisfacimento di vincoli.

La macchina di Boltzmann

fig. 5

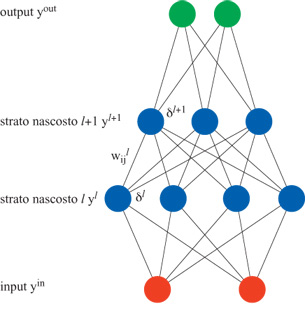
Rappresentazioni interne. - I perceptron hanno capacità limitate, perché possono risolvere soltanto problemi del primo ordine nei loro analizzatori di caratteristiche. Se però introduciamo ulteriori strati di neuroni tra gli strati di input e output (fig. 5), problemi di ordine superiore (come lo XOR) si possono risolvere se le unità nascoste costruiscono (o 'imparano') opportune rappresentazioni interne. La macchina di Boltzmann (Ackley et al., 1985) può avere questo tipo di architettura; a differenza del perceptron, la cui natura è strettamente feedforward (con propagazione in avanti), si hanno connessioni tra i neuroni in entrambe le direzioni, e con uguali intensità, come nel modello di Hopfield. Questo fatto garantisce che la rete rilassi verso uno stato di equilibrio mediante una discesa di gradi ente nell'energia

formula [10]

dove le θi sono ancora le soglie dei neuroni. Questi termini di soglia si possono eliminare ipotizzando che ogni neurone sia connesso a un'unità permanentemente attiva, la cui connessione con il neurone i abbia intensità -θi. L'energia può allora essere espressa nella forma

formula [11]

mentre la differenza di energia tra uno stato in cui l'unità k è inattiva e uno in cui la stessa unità è attiva è pari a

formula [12]

La regola di decisione probabilistica utilizza il rumore per sfuggire dai minimi locali. - Nella macchina di Boltzmann i neuroni non sono caratterizzati da una soglia deterministica, ma da una regola di decisione probabilistica, secondo la quale il neurone k-esimo si trova nello stato Sk = l con probabilità

formula [13]

Il parametro T corrisponde alla temperatura di un sistema fisico. L'output del neurone è sempre 0 o 1, ma la sua distribuzione di probabilità è una sigmoide, cosicché, in media, il suo output assomiglia a una sigmoide. Si noti che quando T tende a zero, la distribuzione si riduce a una funzione a gradino. Questa regola consente al sistema di saltare occasionalmente a configurazioni di energia maggiore (Metropolis et al., 1953), e di sfuggire quindi dai minimi locali. Il dispositivo trae il suo nome dalle proprietà matematiche dei sistemi termodinamici che furono per la prima volta formalizzate da Boltzmann, e che risultano utili anche per la soluzione di problemi di ottimizzazione (Kirkpatrick et al., 1983).

Mentre il modello di Hopfield utilizza i minimi locali come espressione dei ricordi immagazzinati nel sistema, la macchina di Boltzmann usa una simulazione del processo di annealing ('ricottura', o trattamento termico di un sistema allo scopo di raggiungere un minimo globale dell'energia), poiché la probabilità relativa di due stati globali rx e f3 segue la distribuzione di Boltzmann:

formula [14]

e quindi lo stato di energia minima è il più probabile, a qualsiasi temperatura. Il lungo tempo che occorre a raggiungere l'equilibrio termico richiede una tabella di annealing che inizi ad alta temperatura e la riduca gradualmente (Binder, 1978).

Questa procedura è del tutto analoga al processo fisico di annealing di un cristallo con difetti, processo in cui l'alta temperatura fa sì che gli atomi che occupano posizioni irregolari continuino a spostarsi, fino ad assumere una configurazione di equilibrio stabile all'interno del reticolo cristallino. Via via che la temperatura si abbassa, gli atomi si bloccano nelle posizioni giuste. L'effettiva realizzazione di questa procedura di annealing mediante un calcolatore seriale è faticosa per due motivi. In primo luogo, il calcolo richiede di fissare le distribuzioni di probabilità e le leggi fisiche che regolano il movimento delle particelle. In secondo luogo, l'elaborazione avviene in modo seriale. Per le stesse ragioni, anche le simulazioni della macchina di Boltzmann su calcolatori digitali sono difficili da realizzare. Le nostre simulazioni al calcolatore utilizzano l'equazione [11] per calcolare le probabilità di attivazione dei neuroni, mentre nella versione elettronica del modello utilizziamo meccanismi basati sul rumore elettronico per far fluttuare la probabilità di attivazione.

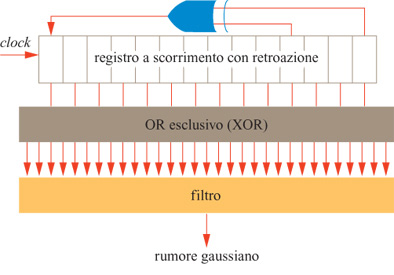
Realizzazione elettronica del rumore. - È utile, nel progettare un sistema elettronico che sia in grado di emulare i neuroni reali, trarre vantaggio dal comportamento fisico dei dispositivi elettronici, sfruttando per quanto possibile il parallelismo. La distribuzione di probabilità sigmoide dell'equazione [11] ha una stretta analogia elettronica in un salto di tensione con rumore. Entro qualche unità percentuale, la probabilità che un neurone con distribuzione sigmoide sia attivo è pari alla probabilità che lo sia un neurone deterministico 'a gradino', se la sua soglia viene perturbata da un rumore gaussiano. Un altro modo di considerare l'annealing consiste quindi nel cominciare con una soglia rumorosa, e ridurre gradualmente il rumore. In uno dei nostri progetti di chip (Alspector et al., 1989) abbiamo provato a sfruttare il rumore termico presente nei circuiti elettronici (Motchenbacher e Fitchen, 1973), che segue una distribuzione gaussiana, ma in seguito ci siamo orientati verso un metodo più robusto, basato su registri a scorrimento con retro azione (Alspector et al., 1991). In elettronica, la generazione parallela del rumore può rendere possibile la realizzazione di una macchina di Boltzmann. Abbiamo anche incorporato l'effetto di annealing legato al rumore senza usare effettivamente il rumore, implementando nel nostro sistema una versione di campo medio della macchina di Boltzmann; descriveremo questi aspetti più avanti (Peterson e Anderson, 1987; Alspector et al., 1992). Un enorme incremento in velocità dell'elaborazione elettronica si ottiene facendo sì che i neuroni determinino il loro stato in modo continuo e asincrono, e che tutte le connessioni modifichino la loro intensità per mezzo di processori distinti, operanti in parallelo.

L'algoritmo di apprendimento e l'importanza dell'informazione locale. - Il problema dell'attribuzione dei meriti (credit assignment), che aveva rallentato lo sviluppo dei perceptron multistrato, si può risolvere, nell'ambito dello schema della macchina di Boltzmann, modificando i pesi in modo tale che vengano utilizzate solo informazioni locali. L'algoritmo di apprendimento prevede due fasi. Nella fase +, o fase bloccata (clamped phase), le unità di input e di output sono fissate in modo da riprodurre un particolare pattern di cui si desidera l'apprendimento, mentre la rete rilassa verso uno stato di bassa energia, aiutata da una tabella di annealing scelta in modo opportuno. Nella fase -, o fase non bloccata (unclamped phase), le unità di output sono lasciate libere, e il sistema rilassa di nuovo verso uno stato di bassa energia, mantenendo gli input fissati. L'obiettivo dell'algoritmo di apprendimento consiste nel determinare un insieme di pesi tali che gli output appresi nella fase - corrispondano il più possibile agli output desiderati. La probabilità che due neuroni i e j siano entrambi nella fase +, Pt, si può determinare contando il numero di volte in cui essi risultano entrambi attivi, mediando su alcuni o tutti i pattern (corrispondenze input-output) nell'insieme di addestramento. Per ogni corrispondenza, si raccoglie anche la statistica analoga per la fase -, calcolando Pij. Entrambi gli insiemi di stime statistiche vengono determinati all'equilibrio termico; dopo aver raccolto una statistica sufficiente si modificano i pesi, secondo la regola

formula, [15]

in cui η riscala la dimensione di ogni cambiamento dei pesi. Si può dimostrare (Ackley et al., 1985) che questo algoritmo minimizza una misura, tratta dalla teoria dell'informazione, della discrepanza tra le probabilità nella fase + e nella fase -. L'algoritmo effettua una discesa di gradiente nella funzione costo

formula [16]

dove la somma su rx è estesa agli stati globali del sistema; P_α⁺ e Pα^- sono le probabilità che si realizzino questi stati nella fase bloccata e in quella non bloccata. In generale, la regola di apprendimento con discesa di gradiente è

formula [17]

e si può dimostrare che da tale regola segue la regola di apprendimento della macchina di Boltzmann (equazione [15]). La minimizzazione di G 'insegna' al sistema a fornire gli output desiderati. Va sottolineato che questa procedura utilizza solo informazioni disponibili localmente (lo stato dei due neuroni) per decidere come aggiornare il peso della sinapsi che connette due neuroni. Ciò rende possibile una realizzazione VLSI in cui i pesi si possono aggiornare in parallelo senza bisogno di alcuna informazione globale (a parte quella riguardante la fase), e malgrado ciò si ottimizza una misura globale dell'apprendimento.

Apprendimento deterministico mediante retropropagazione degli errori nelle reti feedforward

La regola delta generalizzata. - L' algoritmo deterministico più comunemente utilizzato per le reti feedforward, la retropropagazione (Rumelhart et al., 1986), richiede, per risolvere la maggior parte dei problemi, meno tempo di calcolo rispetto all'algoritmo di Boltzmann. La retropropagazione non richiede l'assestamento in uno stato di equilibrio a ogni presentazione di un pattern, che invece è necessario nella macchina di Boltzmann. Vedremo più avanti in che modo la procedura di raggiungimento dell'equilibrio si possa velocizzare mediante la versione di campo medio della macchina di Boltzmann. Anche l' algoritmo di retropropagazione utilizza una generalizzazione della procedura di convergenza del perceptron, in una variante chiamata regola delta, dovuta a B. Widrow e M.E. Hoff (1960).

Questa regola viene applicata a reti del tipo di quella mostrata in figura 5, in cui le connessioni tra i neuroni funzionano solo in una direzione (in avanti). I neuroni sono caratterizzati da una funzione di risposta che varia gradualmente e ha una regione di linearità, come la sigmoide, in modo tale che l'output Yi sia una funzione differenziabile dell'input totale netto al neurone i, Xi. La funzione Yi è semplicemente, nel caso della sigmoide:

formula [18]

Per stati discreti (0, 1), avevamo indicato Xi con ΔEi perché, nella macchina di Boltzmann, la differenza di energia è uguale all'input totale netto. Se identifichiamo gli strati con un indice l, allora:

formula. [19]

Se vi sono l strati di pesi, gli strati di unità sono l + 1. La regola del perceptron per la modifica dei pesi dopo la presentazione di una coppia input-output è

formula, [20]

in cui δ_i^l+1 è l'errore nello strato l + 1, che sarà definito nell'equazione [26]; con

formula [21]

denotiamo il segnale di errore per lo strato di output Questo è il solo strato che può avere un segnale di errore, come è ovvio, se il perceptron ha un solo strato; y_i^out,+ è l'output desiderato sul neurone i, y_i^out,- è l'output effettivamente ottenuto, y^l_j è l'output del neurone j dello strato l che fornisce input al neurone i dello strato l + 1, ed η riscala le modificazioni dei pesi. Questa regola, con la funzione ε da minimizzare uguale all'errore di output, vale quando non vi sono unità nascoste, e gli input inviano segnali direttamente agli output.

In presenza di unità nascoste, si può ricavare una regola di apprendimento che effettua una discesa di gradiente rispetto a una misura dell'errore sulle unità di output. Nella maggior parte dei casi tale misura consiste nella funzione costo quadratica

formula, [22]

che va minimizzata.

La modifica dei pesi lungo la direzione opposta a quella del gradi ente fornisce la relazione

formula. [23]

Calcolando le derivate della funzione costo quadratica per ricavare la regola per il cambiamento dei pesi, l'errore di output risulta:

formula [24]

in cui l'apice denota la derivata prima. Se si impiega una funzione costo più simile a quella utilizzata nella macchina di Boltzmann, derivata da considerazioni di teoria dell'informazione, cioè la funzione

formula [25]

allora l'equazione [21] fornisce l'errore in output. Utilizzando il δ_i^out opportuno nell'equazione [20] si ottiene la regola per la modificazione dei pesi delle connessioni allo strato di output il segnale di errore viene quindi propagato all'indietro per modificare i pesi delle connessioni agli strati nascosti. Per ottenere il segnale di errore relativo alle unità nascoste dello strato l si calcola la quantità

formula, [26]

dove la somma viene effettuata sui segnali di errore delle unità alle quali l'unità considerata invia segnali. Si noti che le 'delta' sommate sono moltiplicate per la derivata della funzione di attivazione. Tale regola vale in qualsiasi caso (a meno che l'unità sia una unità di output), e qualunque sia il numero di strati nascosti. Per la modifica dei pesi si usa l'equazione [20]. Le unità di input, naturalmente, non hanno errore.

La procedura prevede innanzitutto la propagazione in avanti del pattern di input, per calcolare i valori di output y_i̅. Si confronta quindi l' output con quello desiderato e si determina il segnale di errore per ogni unità di output. Tale segnale viene quindi propagato all'indietro in modo ricorsivo, e determina i cambiamenti dei pesi.

Alcune scelte progettuali

fig. 6

Nel decidere quale algoritmo di apprendimento neurale utilizzare, in vista di una realizzazione analogica VLSl, bisogna prendere in esame il modo in cui la retropropagazione e l' algoritmo della macchina di Boltzmann si pongono in corrispondenza con i neuroni e le sinapsi reali. Questa corrispondenza è schematizzata nella figura (fig. 6). Il neurone di Boltzmann (v. figura 6a) effettua una somma degli input (che si può realizzare con una somma in corrente utilizzando la legge di conservazione della carica, cioè la legge di Kirchhoff) e ne usa il risultato come input a una funzione di attivazione non lineare (che si può realizzare mediante un amplificatore). Anche il neurone della rete a retropropagazione (figura 6b) ha la sua somma e la sua funzione di attivazione standard, ma per realizzare fisicamente l' algoritmo servono un ulteriore neurone virtuale e connessioni virtuali per la propagazione all'indietro dell'errore. Questo neurone virtuale riceve i segnali di errore che si propagano all'indietro, che vengono sommati (cosa ottenibile fisicamente, come abbiamo visto, mediante una somma in corrente). L'errore così sommato, però, deve essere moltiplicato per la derivata della funzione di attivazione, e il calcolo esatto di una derivata è difficile da realizzare in VLSI analogico.

La figura 6c mostra il funzionamento di una sinapsi fisica nella macchina di Boltzmann. Essa moltiplica semplicemente le attivazioni dei neuroni da essa connessi (in ciascuna direzione) per il peso memorizzato, e invia in output un contributo all'input netto del neurone ricevente. L'input della sinapsi può essere una tensione (che è l'output dei neuroni, facilmente comunicabile a molte sinapsi), mentre il suo output è una corrente (per facilitare la somma degli input ai neuroni). Nella macchina di Boltzmann i pesi sinaptici sono simmetrici, ma si può dimostrare che l'algoritmo funziona anche quando i pesi sono diversi nelle due direzioni. Dopo il rilassamento (il meccanismo basato sul rumore non è illustrato nella figura) si modificano i pesi secondo la regola di apprendimento illustrata in precedenza, che implica un aggiornamento istantaneo.

In figura 6d è anche mostrato il funzionamento di una sinapsi nella retropropagazione. Il percorso in avanti funziona come nel caso della macchina di Boltzmann. Lo stesso vale per il percorso all'indietro, in cui però ci sono solo connessioni ai neuroni virtuali. l pesi sono anche in questo caso simmetrici nelle due direzioni, ma nel percorso all'indietro si moltiplica l'errore, anziché l'attivazione. La regola di apprendimento combina le informazioni provenienti dall'attivazione (che si propaga in avanti) e dall'errore (che si propaga all'indietro). Nel determinare l'algoritmo più semplice da realizzare abbiamo scelto la macchina di Boltzmann. Le ragioni sono diverse. Per cominciare, non è semplice, in VLSI analogica, calcolare in modo accurato la derivata della funzione di attivazione; la retropropagazione richiede un neurone aggiuntivo e percorsi virtuali; inoltre bisogna mantenere una precisione elevata attraverso tutti gli strati, durante la propagazione all'indietro dell'errore, in modo tale da ottenere una realizzazione digitale di precisione elevata. La regola di apprendimento della macchina di Boltzmann non richiede queste precisioni elevate, perché si basa semplicemente sulla valutazione delle differenze tra la fase bloccata e quella non bloccata. Si noti però che si può usare una regola di apprendimento simile a quella della macchina di Boltzmann, con fasi bloccate e fasi non bloccate, per realizzare un chip basato sulla retropropagazione (Morie e Amemiya, 1994). La parte difficile nella realizzazione della macchina di Boltzmann consiste nell'assicurarsi che le misure di correlazione vengano effettuate in modo non distorto e in condizioni di equilibrio. La tecnica di campo medio costituisce un modo alternativo per raggiungere l'equilibrio.

La versione in campo medio (deterministica) della macchina di Boltzmann. - Indichiamo con Si gli stati digitali delle unità della macchina di Boltzmann, e con Yi le funzioni di attivazione continue della retropropagazione. È da notare che la probabilità di avere uno stato attivo nella macchina di Boltzmann è simile all'attivazione nell' apprendimento della retropropagazione. In realtà usando i metodi di campo medio della fisica è possibile creare un modello approssimato della macchina di Boltzmann chiamato versione di campo medio (Peterson, 1987) o versione deterministica (Hinton, 1989). In questa approssimazione gli stati discreti dei neuroni vengono sostituiti dai loro valori di aspettazione (continui), e questi valori vengono usati come attivazione di output. Quindi la media

formula [27]

diventa

formula. [28]

Se identifichiamo ‹S_i› con l'attivazione Yi, otteniamo:

formula, [29]

che è la stessa funzione di attivazione che tipicamente viene adottata nella retropropagazione eccetto che per il fattore di guadagno β = l/T, dove T è la temperatura.

Nell'approssimazione di campo medio si assume anche che nel calcolo delle correlazioni i valori aspettati si possano fattorizzare,

formula, [30]

anche se spesso questa non è una buona approssimazione.

Pertanto la regola di apprendimento della macchina di Boltzmann

formula [31]

diventa

formula. [32]

Questo modello ha il vantaggio che viene notevolmente ridotto il lungo tempo di annealing che serve ad arrivare all'equilibrio. Invece di diminuire gradualmente la temperatura T (ridurre il rumore), viene aumentato il guadagno β da un valore prossimo allo zero a un valore elevato. Dal punto di vista computazionale questa scelta è più efficiente su un computer (sono richiesti meno cicli per raggiungere l'equilibrio) ed è anche molto naturale per la VLSl, come vedremo. Da notare anche che il modello generale di una sinapsi che integra le covarianze dei neuroni che connette è simile a una regola di tipo hebbiano. La stocasticità è stata usata anche nel lavoro di un gruppo italiano (Badoni et al., 1995) per un modello con apprendimento continuo ispirato al lavoro di Amit e dei suoi collaboratori (v. anche il saggio di D. Amit, P. Del Giudice e S. Fusi, Apprendimento dinamico della memoria di lavoro: una realizzazione elettronica).

La realizzazione elettronica di una macchina di Boltzmann

Il nostro modello incorpora sia la versione stocastica che quella deterministica della macchina di Boltzmann. Il neurone elettronico ha una funzione di attivazione data da

formula [33]

dove f è una funzione non lineare monotona simile a una sigmoide e ν_i è un termine di rumore che si somma all'input xi, indipendente per ogni neurone. Il rumore ha una distribuzione ben approssimata da una gaussiana a media nulla, ottenuta mediante la nostra realizzazione elettronica. Il risultato complessivo è che le Yi seguono con buona approssimazione una distribuzione di Boltzmann. In effetti l'integrale di una gaussiana è la funzione di errore erf(f3xi), che opportunamente riscalata in [l +erf(βxi)]/2 non si discosta che di poche unità percentuali dalla sigmoide. Il rumore può essere diminuito mentre il processo di annealing procede. Se il guadagno β è elevato, il neurone si comporta come la funzione a gradino del modello originale della macchina di Boltzmann.

fig. 7

In figura (fig. 7) viene rappresentato schematicamente il funzionamento del chip con apprendimento, mostrando le funzioni di elaborazione di ognuno dei blocchi. Ogni coppia di neuroni è connessa da una sinapsi. Queste sinapsi emettono una corrente, che viene poi sommata per costruire l'input ai neuroni. l neuroni producono una tensione che è distribuita in parallelo a tutte le sinapsi. Per questo motivo i neuroni hanno basse impedenze di ingresso e di uscita, mentre le sinapsi hanno alte impedenze di ingresso e di uscita. Per ottenere l'annealing in campo medio, il rumore viene fissato a zero mentre viene variato il guadagno β dell'amplificatore del neurone. Volendo, è possibile operare l'annealing utilizzando entrambi i metodi simultaneamente. La media temporale dell'attivazione dei neuroni, cui si aggiungono le fluttuazioni dovute al rumore, coincide con l'attivazione nell'approccio di campo medio.

Al diminuire delle fluttuazioni la media temporale diventa più precisa. In campo medio ciò corrisponde a un aumento del guadagno. Quindi ridurre il rumore nella macchina di Boltzmann stocastica è equivalente ad aumentare il guadagno del neurone in campo medio. La rete viene sottoposta ad annealing nella fase in cui i neuroni sono fissati dall'esterno e nella fase di libera evoluzione, e i pesi vengono aggiornati usando la regola di apprendimento hebbiana:

formula, [34]

misurando le correlazioni dopo la procedura di annealing. l pesi vengono memorizzati con codifica digitale al livello di ogni sinapsi e variano tra -15 e + 15. È possibile ridurre determinati pesi diminuendo l'ampiezza di 1. In ogni neurone la corrente viene sommata sul nodo di input a bassa impedenza insieme al segnale di rumore ottenuto alla fine del processo di annealing, e convertita poi in una tensione. Segue lo stadio di amplificazione della tensione, a guadagno regolabile, che ha caratteristiche non lineari. Questo stadio genera la tensione di uscita, che va poi a tutte le sinapsi. Il risultato di questo processo è la funzione di elaborazione del neurone che è stata descritta in precedenza.

fig. 8

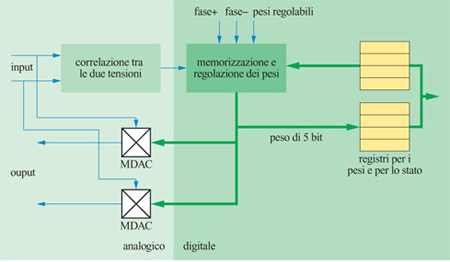
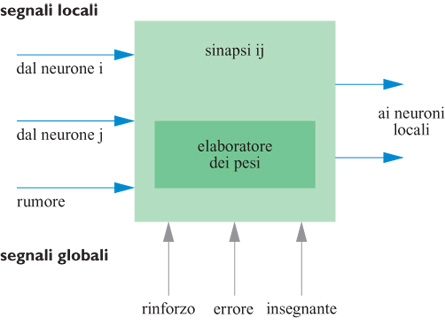
Il diagramma a blocchi della sinapsi viene mostrato nella figura (fig. 8). La sinapsi riceve in input gli output in tensione dei due neuroni che connette. Questo valore in ingresso viene usato in due sedi. Ovviamente viene utilizzato per moltiplicare i pesi nel convertitore digitale-analogico moltiplicatore (MDAC, Multiplying Digital-to-Analog Converter) che produce le due correnti di output. Queste vengono poi sommate agli input dei due neuroni connessi dalla sinapsi. Va notato che queste due correnti sono diverse, perché, sebbene il peso sia lo stesso, nella macchina di Boltzmann le attivazioni dei due neuroni possono essere diverse.

Le tensioni che rappresentano l'attivazione dei neuroni vengono pure moltiplicate l'una con l'altra per creare l'input alla regola di apprendimento hebbiana usata per cambiare i pesi. La correlazione viene memorizzata con un bit (positivo o negativo) e viene calcolata sia nella fase in cui i neuroni sono fissati dall' esterno sia nella fase di evoluzione libera. Se la differenza tra queste correlazioni è positiva, il peso viene aumentato di 1, se è negativa viene diminuito di 1, e se è nulla il peso viene lasciato inalterato.

l pesi sono memorizzati come interi a 5 bit (4 bit più il segno) nei registri CMOS statici, che possono essere aumentati o diminuiti dalla logica circuitale di apprendimento. l pesi possono anche essere scritti e letti come delle SRAM. Altri bit di controllo vengono pure memorizzati in un altro registro. Il generatore di rumore verrà descritto nel seguito.

I microchip con apprendimento

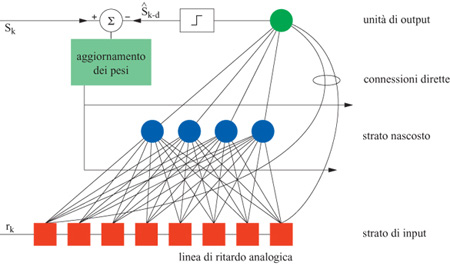
Abbiamo progettato e fabbricato due tipi di prototipi sperimentali di microchip con apprendimento. Uno di essi, detto rete neurale con apprendimento assemblabile in cascata (CLNN32, Cascadable Learning Neural Network) contiene neuroni e sinapsi. L'altro (CLNS64) contiene solo sinapsi, che servono per interconnettere i chip con neuroni. Il CLNN32, mostrato nella figura, contiene 32 neuroni e 992 connessioni (496 sinapsi bidirezionali). Un generatore di rumore fornisce ai neuroni 32 sorgenti scorrelate di rumore pseudocasuale (Alspector et al., 1991). Queste sorgenti di rumore vengono sommate, sotto forma di correnti, ai segnali postsinaptici pesati che provengono da altri neuroni, per realizzare il processo di annealing simulato della macchina di Boltzmann. Gli amplificatori dei neuroni realizzano una funzione di attivazione non lineare che ha un guadagno variabile, come richiesto dalla procedura di annealing nella tecnica di campo medio. L'intervallo in cui varia il guadagno può essere regolato, in modo da riscalare la somma delle correnti quando si cambia la dimensione della rete.

La maggior parte dell'area del chip viene occupata dalla matrice sinaptica. Ogni sinapsi memorizza con una codifica digitale un peso che varia tra -15 e + 15 (4 bit più il segno). Inoltre moltiplica la tensione in ingresso per questo peso, che proviene dal neurone presinaptico per fornire la corrente di output. Una della due direzioni può essere disabilitata, in modo da poter sperimentare cosa accade con reti asimmetriche (Allen e Alspector, 1990). Sebbene si possano scegliere i pesi dall'esterno, le sinapsi sono state progettate per essere adattive. Possono memorizzare correlazioni in parallelo usando la regola di apprendimento locale dell'equazione [34] e aggiornare i propri pesi di conseguenza. La sinapsi considera correlati i due neuroni che connette quando questi sono entrambi attivi (al di sopra di 2,5 V) o inattivi (al di sotto di 2,5 V), e quindi il processore digitale per l'apprendimento in ogni sinapsi assume che lo stato di un neurone sia compreso nell'intervallo che va da -1 a +1.

fig. 9

Per connettere tra loro più chip che contengono neuroni, in modo da formare dei sistemi neurali artificiali più grandi, sono necessari chip che contengono solo sinapsi. I nodi che sommano le correnti dalle sinapsi per produrre l'input dei neuroni nei chip che li contengono sono disponibili esternamente per connettersi ad altri chip, per essere fissati dall'esterno o per connettersi ad altri input esterni. Abbiamo progettato e fabbricato un chip che contiene solo sinapsi (CLNS64) per il nostro microsistema sperimentale. Esso contiene una matrice di 32 x 32 = 1024 sinapsi con apprendimento per connettere i chip contenenti neuroni (fig. 9). Abbiamo integrato questi chip in un prototipo sperimentale di un sistema a 3 chip che contiene 2 chip con neuroni e un chip con sole sinapsi. Questo sistema è equivalente a un sistema con apprendimento con 64 neuroni completamente connessi, e ha un numero di sinapsi pari a 4 volte quelle contenute nel nostro chip con apprendimento con β2 neuroni.

tab. I

Reti più grandi possono essere costruite mettendo in cascata questi dispositivi. Approssimativamente si potrebbero presentare al CLNN32 10⁵ pattem da 32 bitls o 32 canali analogici con una banda limitata a 50 kHz per ogni canale per apprendimento veloce e classificazione. L'insieme di questi chip è stato progettato per essere utilizzato come un sistema di uso generale per la ricerca e la realizzazione di prototipi di applicazioni. Nelle figure 9 e 10 sono mostrate delle microfotografie dei due dispositivi (la scala non è la stessa), e la tabella (tab. I) riassume le caratteristiche chiave delle prestazioni.

Esperimenti di apprendimento

Abbiamo effettuato diversi esperimenti su un sistema che consiste in un singolo chip con apprendimento (Alspector et al., 1992). Per studiare il modo in cui varia l'apprendimento con la dimensione del problema abbiamo scelto i problemi di parità e di replicazione (identità), cosa che facilita il confronto con le nostre simulazioni. Il problema di parità è una generalizzazione del problema dell'OR esclusivo (XOR) per una dimensione arbitraria dell'input (Alspector et al., 1988).

Si tratta di un problema difficile, perché le regioni di classificazione sono disgiunte rispetto a ogni cambiamento di un bit di input, e vi è un solo output. L'obiettivo del problema della replicazione è di duplicare sui neuroni di output il pattem di bit generato dagli input, dopo che è stato codificato nello strato nascosto. Va notato che i bit di output possono essere riordinati in qualsiasi modo, senza che questo cambi la difficoltà del problema. Il numero di neuroni di input e di output deve essere lo stesso. Per il problema di replicazione abbiamo scelto uno strato nascosto con un numero di neuroni pari a quello dello strato di input, mentre per la parità abbiamo scelto uno strato nascosto con un numero di neuroni doppio rispetto allo strato di input.

Abbiamo effettuato esperimenti di apprendimento su chip intervenendo sia sul rumore che sul guadagno per la procedura di annealing. Gli esperimenti sono stati ripetuti sia per il problema della parità che per quello della replicazione, e sono stati usati fino a 8 bit di input, in modo da utilizzare quasi tutti i neuroni di un singolo chip. In questi esperimenti preliminari, per giudicare il comportamento della rete al variare del numero di pattem, abbiamo misurato il numero di pattem necessari per non avere ulteriori miglioramenti nella percentuale di risposte corrette. Questo numero ha un andamento approssimativamente esponenziale rispetto al numero di input per l'apprendimento su chip, esattamente come accadeva nelle simulazioni, dal momento che la dimensione dell'insieme di pattem per l'apprendimento è esponenziale. Complessivamente, il tempo di apprendimento per pattem, sul chip, è molto simile a quello delle nostre simulazioni. Tuttavia, in tempo reale, esso è circa 1000 volte minore per un singolo chip, ed è anche più veloce per sistemi di chip multipli. La velocità, sia per l'elaborazione che per l'apprendimento, è di circa 100 milioni di connessioni al secondo per chip.

La costruzione di sistemi usando chip con apprendimento

Sistema VME e settori di applicazione. - Per permettere un rapido sviluppo di prototipi di applicazioni abbiamo integrato i nostri chip con apprendimento in un computer standard. Il sistema funziona come coprocessore di una workstation, che comunica attraverso un'interfaccia VME per il bus, ed è controllabile con un'interfaccia grafica. Esso utilizza i chip con apprendimento analogico sopra descritti. Sono stati effettuati test su una rete di 3 chip, che consiste di 64 neuroni e circa 1000 sinapsi plastiche. Il sistema serve da piattaforma di test a uso generale per le applicazioni delle reti neurali.

Il sistema coprocessore. - Questo sistema è costituito da tre componenti: la scheda del controllore, le schede per la generazione e acquisizione di pattem analogici e digitali e le schede delle reti neurali. Queste schede costituiscono un sotto sistema VME, che può essere facilmente connesso a una piattaforma di elaborazione a elevate prestazioni. Nella figura (fig. 10) viene mostrato il diagramma a blocchi del sistema.

La scheda del controllore gestisce l'interfaccia VME tra la rete neurale e il computer che la ospita. Il circuito di traduzione degli indirizzi traduce comandi di alto livello in segnali di controllo per i chip della rete neurale. Le funzioni di controllo presenti su questa scheda permettono di gestire varie caratteristiche del sistema: la lettura e scrittura dei pesi; la configurazione della topologia della rete; la procedura di annealing per il rilassamento della rete, sia nel caso di controllo del rumore che nel caso di controllo del guadagno; il controllo dell'apprendimento; l'inizializzazione del generatore di rumore. Questo controllore può controllare fino a 16 chip con reti neurali.

Il sistema di generazione e acquisizione di pattem consiste in una scheda digitale che presenta con la massima velocità ai chip neurali un pattem digitale di input a 64 bit, e ne legge l'output a 32 bit. Schede standard per una rapida conversione multicanale da analogico a digitale, e viceversa, permettono di presentare e acquisire un pattem a 32 canali analogici. l segnali di input e output vengono inviati alle schede con le reti neurali attraverso un bus analogico privato, che serve da bus principale per i pattem della rete. Infine, la scheda della rete neurale (NN, Neural Network) ospita i chip contenenti le reti neurali. Allo stato attuale abbiamo una scheda con 3 chip, ma può essere usato un qualunque numero di schede NN, con l'unico limite imposto dal numero di connessioni instaurabili. Questa scheda è schermata rispetto al bus VME per ridurre l'impatto del rumore, dovuto a commutazioni ad alta velocità, ed è connessa al computer attraverso la scheda del controllore e quella della generazione e acquisizione di pattern mediante il bus di controllo e quello dei pattern (Jayakumar e Alspector, 1993). Essa è interfacciata al bus seriale di una workstation attraverso un adattatore commerciale. L'interfaccia VME è stata scelta perché è uno standard industriale largamente diffuso, e dispone di adattatori per quasi tutte le piattaforme ad alte prestazioni.

La rete neurale a più chip consiste di 2 chip CLNN32 e un chip CLNS64 messi in cascata per formare una rete con 64 neuroni, completamente connessi da 2016 sinapsi. La topologia del sistema garantisce un grado di connessione completo, e, insieme alle sinapsi programmabili, permette di sperimentare diverse architetture di reti neurali; tra queste, le architetture feedforward (il segnale viene propagato in una sola direzione, dai neuroni di input a quelli di output), ricorrenti, a campi recettivi, winner take al! (letteralmente 'il vincitore prende tutto': sono reti dove i pattern di input attivano una sola unità in uscita) e quelle multistrato. È stata prestata particolare attenzione alla schermatura dei chip analogici delle reti neurali, che sono i più sensibili alle interferenze elettriche della scheda su cui sono montati i componenti per il bus VME e gli altri chip digitali della scheda del controllore.

Un esperimento applicativo: equalizzazione non lineare dei canali di comunicazione

Dato che i canali di comunicazione disperdono il segnale nel tempo e nello spazio, il simbolo (o il bit) ricevuto potrebbe essere una quantità analogica, composta da una somma pesata dei simboli (o bit) che stanno attorno al simbolo target. Questa sovrapposizione lineare di simboli può essere sbrogliata mediante un processo noto come equalizzazione. Oggi i modem effettuano l'equalizzazione del canale di comunicazione per migliorare la velocità di trasmissione dati mantenendo un tasso di bit errati (bit error rate) accettabile. La comunicazione digitale usata dai telefoni cellulari permette di effettuare un'equalizzazione simile a livello hardware. È importante, per le applicazioni a sistemi portatili, che l'hardware sia di dimensioni ridotte, abbia bassi consumi e sia economico da produrre. Pertanto abbiamo fatto degli esperimenti per applicare a questo problema i nostri chip con apprendimento. Abbiamo fatto funzionare un sistema di equalizzazione per un canale rumoroso, basato però sull'apprendimento a livello hardware di cui è capace il nostro sistema. Il software presenta solo dei pattern di bit alI 'hardware e mostra i risultati. La rete corregge quasi tutti gli errori dopo alcune migliaia di bit per canali non lineari, e dopo alcune decine di bit per canali lineari.

Il problema dell'equalizzazione di un canale. - Un tipico canale di comunicazione può essere caratterizzato, nella banda base, dalla relazione:

formula. [35]

fig. 11

In questa formula rk è il segnale ricevuto al tempo di campionamento, {Sj} è la sequenza dei simboli trasmessi, {hj} è la risposta del canale, nk è il rumore aggiuntivo durante un periodo di campionamento (si assume che sia rumore bianco gaussiano con varianza σ²) e m = p + q è la memoria del canale. Il secondo termine del membro di destra è l'interferenza intersimbolo (lSI, lnter-Symbol lnterference) causata dagli effetti dispersivi del canale. Nella figura (fig. 11) viene mostrato un equalizzatore lineare adattivo convenzionale. Esso consiste in un filtro a risposta impulsiva finita (FIR, Finite lmpulse Response) con una linea di ritardo, il cui output Sk-d rappresenta una stima del simbolo trasmesso d periodi di campionamento prima:

formula. [36]

Nella relazione precedente W_k^T è un vettore di pesi:

Wk={W0,Wl,...,Wm-l}k [37]

che viene regolato con un algoritrno adattivo allo scopo di minimizzare un'oppurtuna funzione errore. Un esame della figura 11 e dell'equazione [36] rivela una struttura simile a quella di un perceptron con un neurone. La linea di ritardo si trova sullo strato di input, mentre le operazioni di somma e di controllo della soglia sono svolte sul neurone. Questa osservazione porta a chiedersi se le prestazioni di un equalizzatore lineare possano essere migliorate usando neuroni e strati addizionali. L'idea è quella di sfruttare le capacità di trasformazione non lineari, tipiche delle reti neurali, per arrivare a prestazioni superiori rispetto alle tecniche lineari convenzionali. Abbiamo usato il nostro chip della rete neurale per esplorare questa possibilità. Grazie al parallelismo dell' elaborazione il processo è veloce e, siccome può essere realizzato in elettronica analogica, a bassi consumi, il dispositivo può essere anche economico, compatto ed efficiente in termini di potenza assorbita.

I risultati sperimentali

fig. 12

Nella figura (fig. 12) vengono mostrate la struttura dell' equalizzatore e la corrispondenza con gli elementi hardware. L' equalizzatore è costituito da una linea di ritardo analogica, che genera un segnale per lo strato di input. L'output viene trasmesso a un comparatore a soglia ad alto guadagno, che agisce come un decodificatore discriminante. Va notato che la connessione tra lo strato di input e quello di output è diretta. Tutto questo accelera il processo di convergenza, dato che questa configurazione può essere considerata come un equalizzatore lineare che lavora in parallelo a una struttura non lineare.

Per l'esperimento sono stati scelti quattro modelli diversi di canale (Jayakumar e Alspector, 1994), che qui non descriveremo in dettaglio, limitando ci a notare che presentano difficoltà diverse di equalizzazione. Non viene considerata l'interferenza tra canali e si assume che il rumore sia bianco, gaussiano e additivo (AWGN, Additive White Gaussian Noise). In tutti i casi il tasso di bit errati migliora in modo drammatico. Nel caso di canali semplici esso scende di 5 ordini di grandezza dopo poche decine di campioni, mentre nel caso dei canali complessi scende di 2 ordini di grandezza dopo poche migliaia di campioni.

Perché usare un equalizzatore analogico? - La nicchia di mercato per l'utilizzo di chip analogici con apprendimento comprende le applicazioni che richiedono compattezza e bassi consumi, come la comunicazione mobile. Questo rimane vero sia per i canali lineari che per i canali non lineari. In alcuni casi, come per le reti locali senza cavi (WLAN, Wireless Local Area Network), il canale è intrinsecamente non lineare a causa dei ripetitori. In questo contesto potrebbe essere importante usare una tecnica non lineare, come l'adattamento di una rete neurale, per ottenere una trasmissione a larga banda. Inoltre, i bassi consumi dell 'hardware analogico hanno un'importanza cruciale per le applicazioni portatili e mobili.

Una tecnica alternativa per l'apprendimento analogico stocastico

Quando si considera l'apprendimento nei sistemi biologici, dal punto di vista speculativo è utile chiedersi a quale informazione sia disponibile alle sinapsi dal punto di vista dei vincoli fisici. La considerazione di questo problema ci ha portato a preferire la macchina di Boltzmann alla retropropagazione. Inoltre questo punto di vista ci fornisce argomentazioni per andare nella direzione di algoritmi di apprendimento locali, i quali prevedono che la memoria risieda nel luogo dove avviene l'apprendimento, perché nel caso di memoria ad accesso casuale l'energia dissipata sarebbe molto più elevata. Si potrebbe ampliare questo punto di vista domandandosi che cosa possa conoscere una sinapsi fisica dell'intero processo di apprendimento.

fig. 13

Nella figura (fig. 13) viene mostrato il flusso di informazione in una sinapsi fisica. Alcuni input sono segnali locali, consistenti nelle attivazioni dei neuroni connessi dalla sinapsi ed, eventualmente, nel rumore generato localmente. Potrebbero essere disponibili al livello della sinapsi anche dei segnali globali, che in biologia sono dovuti a uno stato generale di 'attivazione' chimica. Questi segnali devono avere una natura generale, non specifica per il neurone o la sinapsi, e dovrebbero includere informazioni sul fatto che un output sia migliore o peggiore (per l'apprendimento con rinforzo ), o sul fatto che l'errore stia diminuendo (per l' apprendimento a discesa di gradiente), o, infine, sul fatto che l'insegnante stia fissando o meno i neuroni in uno stato desiderato (per l'apprendimento alla Boltzmann). L'uscita della sinapsi è diretta solo ai neuroni locali. Va sottolineato che la realizzazione della macchina di Boltzmann soddisfa questo modello locale e globale della sinapsi, dove il rumore viene sommato al livello del neurone (come nella nostra realizzazione), oppure generato a livello della sinapsi e successivamente trasferito al neurone, attraverso il contributo del rumore all'input totale. Il segnale di annealing fa pure parte di questa categoria di segnali non specifici, di natura globale.

Un altro algoritmo di apprendimento compatibile con questo modello sinaptico è quello dell'apprendimento perturbativo. In questo approccio si misura il gradiente (invece di calcolarlo, come nella retropropagazione) perturbando un singolo peso o un singolo neurone (Widrowe Lehr, 1990), e andando a vedere il cambiamento che ne risulta sull' errore del segnale di uscita. Così si ha un criterio per cambiare il peso in modo da seguire il percorso di discesa lungo il gradiente e, allo stesso tempo, restano disponibili tutti i vantaggi dell'utilizzo di neuroni e sinapsi reali per le misure. Questa è la procedura ideale per il VLSI analogico, che, altrimenti, non sarebbe in grado di calcolare con precisione tutte le imperfezioni e le traslazioni di livello. Tuttavia, perturbando un solo peso o un solo neurone alla volta, si perde la capacità di elaborare i pesi in parallelo, che costituisce uno dei vantaggi principali della realizzazione elettronica. D'altra parte, se tutti i pesi vengono perturbati in modo casuale, si può creare un modello di apprendimento parallelo realizzabile in elettronica.

Per rendersene conto bisogna anzitutto notare che si può stimare il gradi ente dell'errore, E (w), rispetto a un generico peso W₁, perturbando W₁ di una quantità δW₁, e misurando di quanto cambia l'errore in uscita δE quando l'intero vettore w, eccetto la componente W1, viene mantenuto costante. Matematicamente:

formula. [38]

Questa procedura di stima può essere effettuata in parallelo osservando che, se tutte le perturbazioni hanno la stessa ampiezza ma segno casuale, allora si può fingere che ogni sinapsi sia l'unica a essere perturbata, e usare la stessa stima del gradiente. Naturalmente il rumore prodotto da queste perturbazioni casuali in parallelo è piuttosto elevato, ma si può mostrare che una tale procedura di apprendimento, in senso probabilistico, converge (Alspector et al., 1993).

Da un punto di vista realizzativo, per creare le perturbazioni casuali si può usare lo stesso generatore di sequenze di bit casuali progettato per la macchina di Boltzmann. Non vi è alcuna necessità di un rumore analogico, ma è sufficiente avere dei bit casuali digitali su ogni sinapsi per scegliere a caso il segno della perturbazione. Siccome il generatore di rumore crea una sequenza di bit casuali, la cui lunghezza varia come l'esponenziale della dimensione del registro a scorrimento con retro azione lineare (LFSR, Linear Feedback Shift Register; v. oltre), la realizzazione di un elevato numero di sinapsi non costituisce un problema. Qui di seguito descriveremo più in dettaglio il generatore di rumore.

La generazione di rumore casuale

Parecchi algoritrni per l'elaborazione neurale dei segnali necessitano della generazione di rumore o di numeri casuali. Abbiamo già discusso l'algoritmo della macchina di Boltzmann e la sua necessità di una procedura di annealing, che prevede l'uso di rumore. Un altro algoritmo che abbiamo trattato è quello dell'apprendimento parallelo perturbativo, nel quale si richiedono perturbazioni casuali e bilanciate per determinare la direzione del gradi ente nello spazio dei pesi. Anche gli algoritmi di apprendimento con rinforzo necessitano di una procedura di ricerca casuale, dal momento che il criterio guida dell'apprendimento si basa solo su un debole segnale scalare, che dice se lo stato attuale è migliore o peggiore di quello precedente.

Vi è anche una vasta classe di realizzazioni, non discusse in questo saggio, in cui l'elaborazione avviene mediante treni di impulsi stocastici, in maniera simile a quanto accade nei neuroni biologici. Se la temporizzazione dei treni di impulsi stocastici è veramente casuale e la densità degli impulsi rappresenta l'attivazione del neurone, allora esiste una realizzazione VLSI particolarmente semplice per la moltiplicazione, l'addizione e l'attivazione (Tomlinson et al., 1990). Più precisamente, la moltiplicazione può essere effettuata con una porta AND, l'addizione con una porta OR, e l'attivazione va in saturazione quando, nei regimi di alta densità di impulsi, due impulsi si sovrappongono. Tuttavia questo richiede un grosso numero di sequenze di bit pseudocasuali che siano effettivamente indipendenti.

Abbiamo condotto uno studio sulla generazione parallela di numeri casuali in VLSI (Alspector et al., 1991). L'obiettivo era di generare un elevato numero di sequenze di bit casuali utilizzando una piccola parte dell'area del chip. La tecnica che abbiamo sviluppato fa uso di un singolo LFSR, ma è in grado di generare un grosso numero di sequenze di rumore in apparenza indipendenti. Un LFSR di una certa lunghezza è in grado di generare una sequenza di bit pseudocasuali (Golomb, 1982). Se si prende questa sequenza di bit e la si integra con un filtro passa-basso, avente una frequenza di taglio pari a poche unità percentuali rispetto alla frequenza di clock, si otterrà l'effetto di integrare la sequenza su molti bit. Se il valore di ogni bit è distribuito in maniera casuale, con probabilità 1/2 di essere O o l, allora il risultato di questa integrazione seguirà una distribuzione binomiale, che approssima una distribuzione gaussiana per un numero elevato di bit. È questo il principio che sta dietro alla sorgente di rumore gaussiano usata nella realizzazione elettronica della macchina di Boltzmann.

Un LFSR a N stadi è in grado di generare una sequenza casuale di bit di lunghezza massima pari a 2N - l, quando i segnali di retro azione sono scelti in modo opportuno (Golomb, 1982). Una utile proprietà di queste sequenze è che hanno una correlazione mutua (cross correlation) trascurabile con la versione traslata nel tempo delle sequenze stesse. Ai fini dell' annealing, questo significa che la traslazione temporale deve essere abbastanza grande perché la rete rilassi a sufficienza e 'dimentichi' la sequenza comparsa in un ciclo di annealing prima di vedere un'altra versione della stessa sequenza. Questa condizione di non sovrapposizione viene facilmente ottenuta con un registro a scorrimento (shift-register), perché allora la lunghezza della sequenza cresce esponenzialmente con la dimensione del registro.

La traslazione potrebbe essere realizzata usando un insieme di LFSR identici, uno per ogni neurone nel caso dell'apprendimento della macchina di Boltzmann, e uno per ogni sinapsi nel caso dell'apprendimento perturbativo. Ogni LFSR verrebbe caricato con uno stato iniziale specifico per ottenere la traslazione desiderata rispetto agli altri LFSR. Tutti gli LFSR verrebbero poi attivati simultaneamente da uno stesso clock. In questo caso lo spreco di risorse è inaccettabile, e come risultato finale il generatore di rumore potrebbe occupare la maggior parte del chip, invece che solo il 2% dell'area.

fig. 14

Abbiamo sviluppato un metodo per usare un registro a scorrimento singolo per sequenze di bit con diverse traslazioni. L'idea viene illustrata nella figura (fig. 14). La logica combinatoria, sotto forma di porte XOR, effettua un'addizione modulo 2 sui segnali, scelti opportunamente da un registro di scorrimento di lunghezza massima. Il risultato complessivo è una serie di traslazioni, di lunghezza (in bit) arbitraria, della sequenza principale. Il filtro passa-basso fornisce poi il rumore gaussiano.

Gli scenari futuri per i sistemi elettronici neurali

Gli anni Novanta sono stati testimoni di un elevato numero di lavori di ricerca e di un numero di gran lunga più ridotto di tentativi di commercializzazione dei chip basati su reti neurali. Gli scenari futuri saranno guidati da motivazioni simili a quelle dei lavori passati. Da un lato emergeranno probabilmente nuove frontiere della ricerca, spinte dagli sviluppi della biologia, dalle nuove tecnologie e dai sistemi su larga scala. Dall'altro, applicazioni interessanti ed economicamente vantaggiose potranno condurre a un successo commerciale.

Le frontiere della ricerca

In alcuni gruppi di ricerca vi è la tendenza a usare l'elettronica per emulare i circuiti neuronali biologici nel tentativo di comprenderli.

Cadono in questa categoria di ricerca i circuiti che imitano la retina e la coclea, e i neuroni di silicio (Mahowald, 1994). Anche se le equazioni di Hodgkin-Huxley, simulate su computer, forniscono buoni modelli dei neuroni biologici, la quantità di elaborazione richiesta è enorme. Alcuni gruppi di ricerca usano supercomputer paralleli per riprodurre i processi di pochi neuroni. Un buon modello elettronico può enormemente accelerare l'elaborazione, e portare a una migliore comprensione. Inoltre problemi quali la dissipazione di potenza, il raffreddamento e il cablaggio si presentano sia nella biologia che nell' elettronica analogica, mentre vengono ignorati nelle simulazioni al computer. È probabile che dalla costruzione di sistemi neurali sempre più grandi emergeranno idee preziose.

È anche lecito attendersi che questi sforzi vengano ulteriormente stimolati dallo sviluppo di nuove tecnologie elettroniche. Ciò potrà avvenire sia se lo sviluppo sarà finalizzato specificamente alle reti neurali, sia se si rivolgerà verso altre applicazioni. Un esempio di queste tecnologie è dato dalla memorizzazione dei pesi sinaptici analogici. È probabile che le tecniche sviluppate per i pesi sinaptici verranno adottate per le dRAM standard, in modo da aumentare la densità di pesi digitali memorizzati. Vi sono articoli recenti che discutono la realizzazione di chip capaci di memorizzare 2 bit per ogni cella dRAM (Murotani, 1997). Questa tecnica di progettazione potrebbe diventare necessaria in futuro, dal momento che la tecnologia MOS si sta avvicinando ai limiti di circa O, l μm (larghezza minima delle piste realizzabili sul chip). Oltre questo limite saranno necessari degli approcci innovativi per risolvere i problemi di densità con le dRAM (come la memorizzazione di più bit per cella). Il limite è probabilmente attorno a 8 bit per cella. Naturalmente celle di questo tipo richiedono una procedura di refresh a più bit delle celle, ma le tecniche per raggiungere questi scopi sono note. Per evitare il refresh si possono usare memorie capacitive non volatili, adottando la tecnologia dei floating gate.

fig. 15

Uno scenario in cui siano realizzabili sinapsi di dimensioni estremamente ridotte (ricordiamo che le sinapsi occupano gran parte dell'area, in un chip con apprendimento), apre la possibilità di costruire sistemi neurali su larga scala, con milioni di sinapsi per chip e più. Questo numero può essere ulteriormente aumentato usando sistemi a più chip o riscalando la tecnologia, oppure con entrambe le tecniche. Tali sistemi sono già stati realizzati nel sistema di apprendimento della macchina di Boltzmann (Alspector et al., 1991) e nel sistema digitale CNAPS (Hammerstrom, 1991). È possibile che, nei sistemi neuronali, la sola dimensione possa fare la differenza? In linea di principio la risposta è affermativa. La figura (fig. 15), adattata da un recente studio dell'Agenzia per progetti di ricerca avanzati della difesa statunitense (DARP A, Defence Advanced Research Projects Agency) mostra un grafico con le prestazioni di varie applicazioni, sistemi di elaborazione e animali in termini di CPS e numero di connessioni (DARPA, 1988).

Si può vedere che le applicazioni a sistemi di visione complessi richiedono più potenza di calcolo di quanta ne sia disponibile allo stato attuale. Inoltre le capacità del cervello umano sono ben al di fuori della portata dei sistemi elettronici di oggi. Naturalmente la pura potenza di calcolo, da sola, è insufficiente per creare un'intelligenza simile a quella umana. Lo stretto accoppiamento tra i sensori neuronali e gli effettori, le mappe neuronali del cervello, e una miriade di altri dettagli sono senza dubbio responsabili della stupefacente versatilità dell'intelligenza umana. Tuttavia ad alcuni livelli la potenza di calcolo entrerà certamente in gioco. Gli sforzi mirati a 'costruire un cervello' su larga scala andranno di pari passo con la comprensione delle architetture neuronali. Forse l'interesse attuale verso la coscienza stimolerà ulteriormente questi sforzi, per verificare se un sistema neurale abbastanza grande sia effettivamente in grado di elevarsi a tale stato.

Le frontiere delle applicazioni

Sebbene la gran parte delle applicazioni disponibili richiedano solo delle reti neurali software, compariranno sempre più nicchie di mercato in cui saranno necessarie le reti neurali hardware. Questo accadrà per la necessità di migliori prestazioni, di dimensioni più ridotte e di consumi più bassi.

È probabile che i sistemi visivi saranno un elemento trainante per le risorse computazionali disponibili solo in realizzazioni hardware. Forse questi sforzi dovrebbero essere guidati dal motto "tanti pixel in poco tempo". Se i sistemi di visione artificiale basati sui computer vengono posti di fronte al problema di trovare dei pattem in una scena visiva, essi falliscono, in parte per la loro debolezza sul fronte della potenza di calcolo. Per esempio, il chip NilOOO viene usato per controllare il traffico automobilistico usando telecamere standard (Holler et al., 1992). La potenza di calcolo fornita da questo chip con funzioni specifiche è strettamente sufficiente per il compito per cui esso è stato costruito. L'elaborazione più raffinata delle immagini video del traffico di un'autostrada richiederà notevoli progressi nei sistemi a più chip, o addirittura la creazione di nuovi chip. Si possono immaginare esigenze simili per il controllo di qualità dei prodotti, il controllo del traffico aereo, e i sistemi di sicurezza degli aeroporti. I sistemi neurali saranno anche necessari per l'elaborazione di documenti, per trovare scene specifiche in un film, per i sistemi di sorveglianza continua e le transazioni, per scoprire le frodi e per gestire il traffico delle telecomunicazioni.

Inoltre, dal momento che i computer standard diventano sempre più complessi, il riconoscimento della voce e dei pattem contribuiranno a migliorare l'interfaccia con l'utente. Per esempio, alcuni sistemi palmari dispongono già di un sistema di input con una penna, basato sul riconoscimento dei caratteri, scritti a mano, tramite una rete neurale. I bassi consumi e le dimensioni compatte saranno alla base di molte applicazioni. È già partito un progetto per costruire un naso elettronico neuromorfo che, secondo quanto previsto, dovrebbe avere un processore elettronico neurale addestrabile per classificare gli odori.

Abbiamo già discusso l'uso di chip con apprendimento per l' equalizzazione di canali. Questi e altri usi sono molto adatti per applicazioni portatili, dove le realizzazioni in elettronica analogica mostrano i loro punti di forza. Come possiamo vedere, nonostante la mancanza, finora, di un successo commerciale, le aree di applicazione previste sono numerose e interessanti. Gli scenari futuri per questo tipo di ricerca appaiono molto promettenti.

Bibliografia citata

ACKLEY, D.H., HINTON, O.E., SEJNOWSKI, T.J. (1985) A leaming algoritlnn for Boltzmann machines. Cognit. Sci., 147-169.

ALLEN, R.B., ALSPECTOR, J. (1990) Learning of stable states in stochastic asymmetric networks. IEEE Transanctions on Neural Networks, 1, 233-238.

ALSPECTOR, J., ALLEN, R.B., HU, V., SATYANARAYANNA, S. (1988) Stochastic learning networks and their electronic implementation. In Proceedings of the conference on neural inJormation processing systems, a c. di Anderson D., New York, Am. Inst. of Phys.

ALSPECTOR, J., GANNETT, J.W., HABER, S., PARKER, M.B., CHU, R. (1991) A VLSI-efficient technique for generating multiple uncorrelated noise sources and its application to stochastic neural networks. IEEE Trans. Circuits & Systems, 38, 109.

ALSPECTOR, J., GUPTA, B., ALLEN, R.B. (1989) Performance of a stochastic learning microchip. In Advances in neural information processing systems 1, a c. di Touretzky D.S., San Mateo, Morgan Kaufmaun.

ALSPECTOR, J., JAYAKUMAR, A., LUNA, S. (1992) Experimental evaluation of leaming in a neural microsystem. In Neural information processing systems 4, a c. di Moody J.E., Hanson S.I., Lippmaun R.P., San Mateo, Morgan Kauffman, pp. 871-878.

ALSPECTOR, J., MEIR, R., YUHAS, B., JAYAKUMAR, A., LIPPE, D. (1993) A parallel gradient descent method for leaming in analog VLSI neural networks. In Neural information processing systems 5, San Mateo, Morgan Kauffman, pp. 836-844.

ANDERSON, J.A., SILVERSTEIN, J.W., RITZ, S.A., JONES, R.S. (1977) Distinctive features, categorical perception, and probability learning: some applications of a neural model. Psych. Rev., 84, 413-451.

BADONI, D., BERTAZZONI, S., BUGLIONI, S., SALINA, G., AMIT, D.J., FUSI, S. (1995) Electronic implementation of an analogue attractor neural network with stochastic learning. Network Computation in Neural Systems, 6, 125-157.

BINDER, K., a c. di (1978) The Monte-Carlo method in statistical physics. New York, Springer Verlag.

BOAHEN, K. (1996) Retinomorphic vision systems. Proceedings of MicroNeuro 96, 2.

COGGINS, R.J., JABRI, M.A., FLOWER, B.F., PICKARD, S.J. (1995) A hybrid analog and digital neural network for intracardiac morphology classification. IEEE Journal of Solid-State Circuits, 305, 542-550.

COHEN, M.A., GROSSBERG, S. (1983) Absolute stability of global pattern formation and parallel memory storage by competitive neural networks. Trans. IEEE SMC, 13, 815.

DARPA (1988) Neural network study. Fairfax AFCEA International Press.

GOLOMB, S.W. (1982) Shift register sequences. Laguna Hills, Aegean Park Press.

GRAF, H.P., et al. (1986) VLSI implementation ofa neural network memory with several hundreds of neurons. In Proceedings of the Conference on neural networks for computing, New York, Am. Inst. of Phys., p. 182.

GROSSBERG, S. (1969) On learning and energy-entropy dependence in recurrent and nonrecurrent signed networks. J. Stato Phys., 1, 319.

GROSSBERG, S. (1973) Contour enhancement, short term memory, and constancies in reverberating neural networks. In Studies in applied mathematics LII. Cambridge, Mass., MIT Press.

HAMMERSTROM, D. (1991) A highly parallel digital architecture for neural network emulation. In VLSI for artificial intelligence and neural networks, a c. di Delgado-Frias lG., Moore W.R., New York, Plenum Press, pp. 357-366.

HEBB, D.O. (1949) The organization of behavior. New York, Wiley.

HINTON, G.E. (1989) Deterministic Boltzmaun learning performs steepest descent in weight space. Neural computation, 1, 143150.

HOLLER, M., PARK, C., DIAMOND, J., SANTONI, D., THE, S.C., GLIER, M., SCOFIELD, C. L. , NUNEZ, L. (1992) A high performance adaptive classifier using radiaI basis functions. In Proceedings of government microcircuit applications conference, Las Vegas.

HOLLER, M., TAM, S., CASTRO, H., BENSON, R. (1989) An electrically trainable artificial neural network (ETANN) with 10240 'floating gate' synapses. In International joint conference on neural networks (IJCNN), vol. II, pp. 191-196.

HOPFIELD, J.J. (1982) Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA, 79, 2554-2558.

JAYAKUMAR, A., ALSPECTOR, J. (1993) An analog neural network co-processor system for rapid prototyping of telecommunications applications. In IEEE/INNS international workshop on application of neural networks to telecommunications, Princeton, e in Proceedings of the international workshop on application of neural networks to telecommunications. Hillsdale, Erlbaum Associates, pp. 13-19.

JAYAKUMAR, A., ALSPECTOR, J. (1994) A neural network based adaptive equalizer for digital mobile radio. In Government microelectronics applications conJerence, San Diego.

KIRKPATRICK, S., GELATT, C.D., VECCHI, M.P. (1983) Optimization by simulated annealing. Science, 220, 671-680.

KIRKPATRICK, S., SHERRINGTON, D. (1978) Infinite-ranged models of spin-glasses. Phys. Rev., 17, 4384-4403.

KOHONEN, T. (1977) Associative memory - A system-theoretic approach. Berlino, Springer Verlag.

McCULLOCH, W.S., PITTS, W.H. (1943) A logical calculus ofideas immanent in nervous activity. Bulletin of mathematical biophysics, 5, 115.

MAHOWALD, M. (1994) An analog VLSI stereoscopic vision system. Boston, Kluwer Academic Publishers.

MEAD, C. (1989) Analog VLSI and neural systems. Menlo Park, Addison Wesley.

METROPOLIS, N., ROSENBLUTH, A., ROSENBLUTH, M., TELLER, A., TELLER, E. (1953) Equation-of-state calculations by fast computing machines. Jour. Chem. Phys., 6, 1087.

MINSKY, M., PAPERT, S. (1969) Perceptrons. Cambridge, Mass., MIT Press.

MORIE, T., AMEMIYA, Y. (1994) An all-analog expandable neural network LSI with on-chip backpropagation learning. IEEE Journal Solid-State Circuits, 29, 1086.

MOTCHENBACHER, C.D., FITCHEN, F.C. (1973) Low noise electronic designo New York, Wiley, p. 9.

MUROTANI, T. et al. (1997) A 4-level storage 4 Gb DRAM. In Digest of technical papers of the 1997 international solid-state circuits conference, p. 74.

PETERSON, C., ANDERSON, J.R. (1987) A mean field leaming algorithm for neural networks. Complex systems, 1:5, 995-1019.

ROSENBLATT, F. (1961) Principles of neurodynamics: perceptrons and the theory of brain mechanisms. Washington, Spartan Books.

RUMELHART, D.E., HINTON, G.E., WILLIAMS, R.J. (1986) Learning internaI representations by error propagation. In Parallel distributed processing: explorations in the microstructure of cognition, a C. di Rumelhart D.E., McClelland J.L., vol. 1. Cambridge, Mass., MIT Press, p. 318.

SEJNOWSKI, T.J. (1981) Skeleton filters in the brain. In Parallel models of associative memory, a c. di Hinton G., Anderson J.A., Hillsdale, Erlbaum Associates, pp. 189-212.

SIVILOTTI, M., EMERLING, M., MEAD, C., NOVEL, A. (1985) Associative memory implemented using collective computation, Proceedings of the 1985 Chapel Hill conference on very large scale integration, p. 329.

TOMLINSON, M.S., WALKER, D.J., SIVILOTTI, M.A. (1990) A digital neural network architecture for VLSI. In Proceeding of the international joint conference on neural networks (IJCNN '90), vol. II, San Diego, pp. 545-550.

WIDROW, B., HOFF, M.E. (1960) Adaptive switching circuits. In Inst. of radio engineers, western electric show and convention, Convention Record, Part 4, 96-104.

WIDROW, B., LEHR, M.A. (1990) 30 years of adaptive neural networks, perceptron, madaline and backpropagation. Proc. IEEE, 78, 1415-1422

INFORMATICA APPLICATA in Informatica
BIOINGEGNERIA in Biologia