distanza
distanza
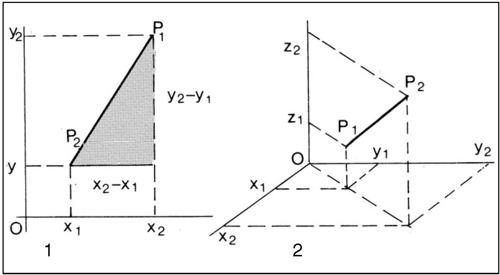
distanza nel suo significato più immediato esprime una misura della lontananza tra due punti o due oggetti geometrici qualsiasi. Nel caso di due punti nello spazio euclideo, la distanza è data dalla lunghezza del segmento che li congiunge ed è a tale caso che si riconduce la definizione e determinazione della distanza tra punto e retta, punto e piano, retta e retta, retta e piano, piano e piano. Nel piano, dotato di un riferimento cartesiano, la distanza tra due punti A(x0, y0) e B(x1,y1) è il numero reale non negativo d a essi associato in base al teorema di Pitagora, dato da:
La definizione e la formula si estendono naturalmente allo spazio euclideo Rn applicando più volte il teorema di Pitagora e quindi considerando la radice quadrata della somma dei quadrati delle differenze delle rispettive n coordinate dei punti. In tale caso, dati i punti A(x1, x2, ..., xn) e B(y1, y2, ..., yn) si ha:
La distanza così definita viene detta distanza euclidea o anche distanza pitagorica, in quanto si ottiene applicando n − 1 volte il teorema di Pitagora. Entrambe le formule rappresentano la lunghezza del segmento AB e corrispondono cioè all’idea intuitiva di distanza nel piano e nello spazio.
Il concetto di distanza euclidea viene generalizzato introducendo la curva geodetica definita come il più breve cammino tra due punti di uno spazio. Nel piano e nello spazio euclidei le geodetiche sono linee rette, mentre su una superficie sono in generale delle linee curve. Le geodetiche di una superficie sferica sono costituite da circonferenze di raggio massimo. La distanza tra due punti di una superficie è data dalla lunghezza del tratto di geodetica che li congiunge. Sulla superficie di una sfera la distanza tra due punti A e B può essere definita non solo come lunghezza del più corto dei due archi di cerchio massimo per A e B (tratto di geodetica), ma anche come distanza angolare, cioè come ampiezza dell’angolo non concavo avente il vertice nel centro della sfera e i lati passanti per A e B. Sulla superficie terrestre la latitudine e la longitudine di un punto P sono, rispettivamente, la distanza angolare (con segno) di P dall’equatore e dal meridiano fondamentale.
Una ulteriore generalizzazione si ha introducendo, in uno spazio euclideo la p-distanza, definita, dati i punti A(x1, x2, ..., xn) e B(y1, y2, ..., yn), come segue:
Se p = 2 si ha come caso particolare la distanza euclidea; se p = 1 e n = 2 (si è cioè nel piano) la distanza è detta distanza del taxista, perché esprime la distanza misurata su un reticolato a maglie rettangolari, come fossero le strade di una città dalla struttura reticolare; tale distanza genera una geometria diversa, detta geometria del taxi.
In termini astratti e del tutto generali si definisce metrica su un insieme X qualsiasi funzione d: X × X → R tale che, per ogni x, y, z ∈ X valgano le seguenti proprietà:
La coppia (X, d) è detta spazio metrico. Il valore della funzione d per ogni coppia (x, y) di elementi di X è detta distanza tra x e y.