distribuzione binomiale
distribuzione binomiale
Sia Y1,Y2,... una successione di variabili casuali indipendenti, ciascuna delle quali può assumere solo i valori 0 e 1 con probabilità rispettivamente pari a p e 1−p, con 0≤p≤1. Una semplice realizzazione di questo schema è rappresentata da lanci successivi di una moneta, associando convenzionalmente il valore 1 a ogni ‘testa’ e 0 a ogni ‘croce’. Ciascuna delle due possibilità è considerata equiprobabile e il valore del parametro p è pertanto fissato a 1/2. Se il numero di variabili Yi (ovvero di lanci) è fissato e pari a n si parla allora di esperimento di Bernoulli. La probabilità che la variabile casuale X=Y1+...+Yn assuma il valore k (con k≤n), ovvero che in n lanci si ottengano k teste (o croci), è allora pari a
dove
]è detto coefficiente binomiale. La distribuzione di probabilità [[[:File:VOL_6_distribuzione_binomiale_03.jpg|3]]] è detta distribuzione binomiale. Essa è data dalla formula
Il suo primo momento (ovvero il valore atteso della variabile X) è dato da
il secondo (la varianza di X) da
]
=np(1−p).
Se n (il numero di lanci) tende a infinito, il teorema di De Moivre-Laplace stabilisce che è possibile esprimere la distribuzione binomiale in termini della distribuzione normale Φ(x). Più precisamente, abbiamoP iP
dove Rn tende a zero al crescere di n.

![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/6/60/VOL_6_distribuzione_binomiale_01.jpg)
![[2]](https://images.treccani.it/ext-tool/intra/thumbs_medium/d/d8/VOL_6_distribuzione_binomiale_02.jpg)
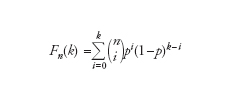
![[4]](https://images.treccani.it/ext-tool/intra/thumbs_medium/e/e1/VOL_6_distribuzione_binomiale_04.jpg)
![[5]](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/7d/VOL_6_distribuzione_binomiale_05.jpg)
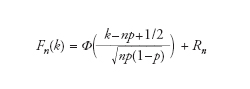
![[7]](https://images.treccani.it/ext-tool/intra/thumbs_medium/5/57/VOL_6_distribuzione_binomiale_07.jpg)