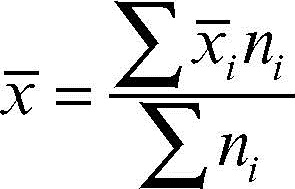distribuzione continua

distribuzione continua

distribuzione continua in statistica e probabilità, distribuzione di una variabile che può assumere un numero infinito di valori tra due distinte modalità. Sul piano metodologico, occorre distinguere tra → variabili statistiche e → variabili aleatorie.

Distribuzione continua di una variabile statistica

Si dice che un carattere statistico ha una distribuzione continua se, comunque si prendano due valori all’interno dell’intervallo in cui il carattere è osservato, tutti i valori intermedi possono essere assunti come modalità del carattere stesso; tali sono per esempio l’altezza o il peso relativi a un insieme di individui. Da un punto di vista descrittivo, un carattere continuo può, per definizione, assumere infiniti valori e le modalità di tale carattere sono allora generalmente raggruppate in classi: l’insieme delle coppie formate dalle classi con le relative frequenze costituisce una distribuzione, detta anche seriazione statistica continua. Ogni classe è un intervallo, chiuso soltanto a destra oppure soltanto a sinistra, ed è caratterizzata da una ampiezza, cioè dalla differenza fra il suo estremo superiore e quello inferiore. Ogni classe c_i è quindi caratterizzata da alcuni parametri, che ne consentono l’utilizzo per ulteriori elaborazioni e per definire alcuni elementi di tale distribuzione continua:

• l’ampiezza: α_i = x_i+1 – x_i;

• la densità di frequenza, vale a dire il rapporto tra la frequenza e l’ampiezza della classe d_i = n_i /a_i, dove n_i è la frequenza della classe c_i;

• l’intensità complessiva di classe, ossia il totale complessivo delle modalità presentate dalle singole unità appartenenti alla stessa classe, la cui stima è data da x̄_in_i, in cui x̄_i è la media della classe.

Utilizzando l’intensità complessiva di classe è possibile calcolare o stimare la media aritmetica della variabile statistica. Se l’intensità complessiva di una classe è conosciuta, allora basta calcolare il rapporto tra tutte le intensità e il totale delle frequenze. Se invece non si conosce l’intensità di classe, allora si può soltanto stimarne la media, attraverso il modello:

detta media di una distribuzione continua.

Distribuzione continua di una variabile aleatoria

Una variabile aleatoria X a valori in un sottoinsieme S di R ha una distribuzione continua se per ogni valore x di S la probabilità è nulla: P(X = x) = 0 per ogni x ∈ S. Questo fatto, apparentemente paradossale, si spiega in diversi modi: in termini intuitivi, se si considera un bersaglio circolare, il suo centro geometrico è solo uno tra gli infiniti punti del bersaglio e dunque, secondo l’interpretazione classica, la probabilità di colpirlo con una freccetta è 1/∞, cioè 0. Più formalmente, interpretando la probabilità come misura e, in particolare, come misura della superficie sottesa alla funzione di densità di probabilità della variabile, una “superficie” la cui base è un punto non può che avere area nulla: per tale motivo si utilizza la nozione di densità di probabilità in un intervallo. Un esempio di distribuzione continua è la → distribuzione normale.