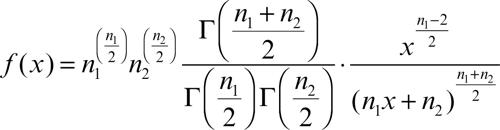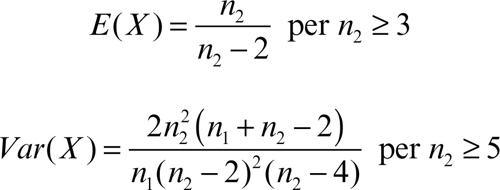Fisher, distribuzione F di
Fisher, distribuzione F di
Fisher, distribuzione F di distribuzione di probabilità di una variabile aleatoria continua completamente determinata da due parametri: i gradi di libertà delle distribuzioni chi-quadrato a partire dalla quale essa è costruita. Fu così denominata dallo statistico statunitense G.W Snedecor in onore del suo maestro R.A. Fisher. La variabile aleatoria F si ottiene come rapporto di due variabili aleatorie chi-quadrato tra loro indipendenti divise per i rispettivi gradi di libertà n1 e n2 e spesso è indicata con F(n1, n2). La sua funzione di densità è ƒ(x) = 0 se x ≤ 0 e, se x > 0, è
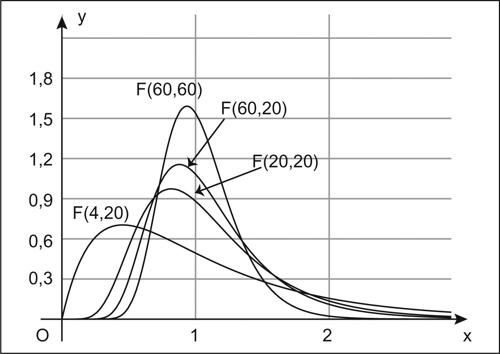
dove Γ è la funzione gamma di Eulero. La forma del suo grafico, comunque asimmetrico, varia molto a seconda dei valori dei due parametri n1 e n2. Il valore medio E(X) e la varianza Var(X) della distribuzione F di Fisher non sono sempre definiti. Si ha:
Essa descrive l’andamento del rapporto tra le varianze delle due distribuzioni in funzione dei loro gradi di libertà ed è principalmente utilizzata per verificare la differenza statistica tra le due varianze.
