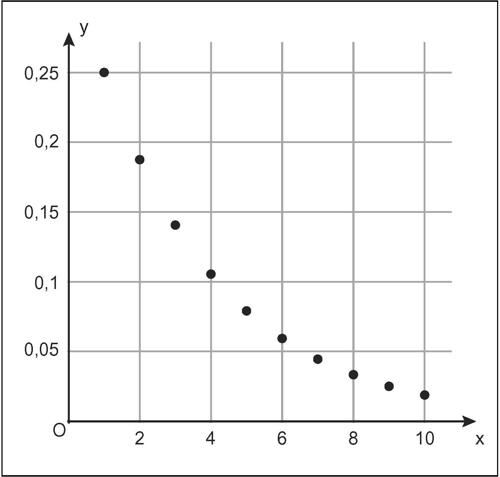
distribuzione geometrica

Enciclopedia della Matematica (2013)

distribuzione geometrica distribuzione di probabilità di una variabile aleatoria discreta X sotto le seguenti condizioni:

• si ha una successione di prove indipendenti;

• in ogni prova ci sono due possibili risultati (successo o insuccesso) e il successo si verifica con probabilità costante uguale a p;

• X esprime il numero di prove necessarie per avere il primo successo.

Poiché il primo successo si ha alla ennesima prova solo se nelle prime n − 1 prove indipendenti si è avuto un insuccesso, si ha: P(X = 1) = p, P(X = 2) = (1 − p)p e, in generale, p(X =n) = p(1 − p)ⁿ⁻¹ per n = 1, 2, ... La distribuzione geometrica associata al conteggio del primo successo, che ha come unico parametro p, è così detta perché i termini della successione p(1 – p)ⁿ⁻¹ costituiscono una progressione geometrica di ragione q = 1 − p. La media e la varianza di una variabile aleatoria X con distribuzione geometrica di parametro p sono rispettivamente:

distribuzione geometrica

Enciclopedia della Scienza e della Tecnica (2008)

Luca Tomassini Sia data una successione bernoulliana di eventi, cioè una successione di eventi indipendenti in ciascuno dei quali la probabilità di successo è p e quella di insuccesso q=1−p (per es. una serie di lanci di una moneta, con p=1/2). La variabile casuale X uguale al numero di eventi antecedenti ...