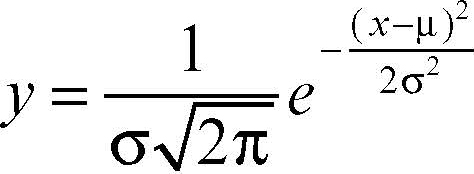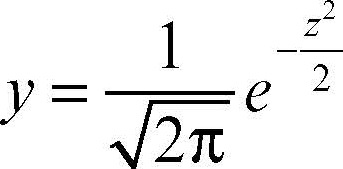distribuzione normale

distribuzione normale

distribuzione normale distribuzione di probabilità relativa a una variabile aleatoria continua, di fondamentale importanza in statistica e probabilità sia perché costituisce una buona approssimazione di altre distribuzioni (per esempio della distribuzione binomiale quando il numero delle prove è grande) sia soprattutto perché, sotto condizioni molto generali, la somma di n variabili casuali indipendenti converge a una distribuzione normale, come stabilito dal teorema del → limite centrale. Per esempio, la distribuzione delle altezze della popolazione adulta maschile di una regione omogenea è influenzata da diversi fattori e complessivamente, se si considera un numero sufficientemente alto, presenta un’altezza media vicina o coincidente con l’altezza di maggiore frequenza (→ moda) e, via via, simmetricamente e regolarmente, con frequenze sempre più basse, individui di altezza minore o maggiore. La distribuzione assume perciò l’andamento di una curva a forma di campana (→ curva normale).

Introdotta da A. de Moivre nello studio dei giochi d’azzardo come distribuzione limite all’aumentare del numero delle prove della distribuzione binomiale, tale distribuzione fu riscoperta da C.F. Gauss come distribuzione degli errori di misurazione e per questo è anche detta distribuzione di Gauss. Deve la sua diffusione in campo statistico a L.-A. Quételet. La base empirica della distribuzione normale si fonda sull’osservazione secondo la quale in natura misurazioni successive di valori caratteristici sono tali che gli errori positivi di misurazione sono in genere numerosi quanto quelli negativi e gli errori piccoli in valore assoluto sono più frequenti di quelli grandi. Ciò porta a una distribuzione degli errori la cui rappresentazione dà luogo a un grafico simmetrico approssimabile appunto con una curva a campana.

La curva è il grafico della funzione

che rappresenta pertanto la funzione di densità di una variabile aleatoria con distribuzione normale (detta anche variabile normale). Essa ha media E(X) = μ e varianza Var(X) = σ² e questi costituiscono i suoi due parametri fondamentali. Una variabile con distribuzione normale e di parametri μ e σ è anche indicata con N(μ, σ) o Norm(μ, σ). La funzione presenta le seguenti caratteristiche:

• è definita per ogni valore reale di X e assume valori sempre positivi;

• è simmetrica rispetto alla retta X = μ, cioè rispetto al valore medio della distribuzione, e assume il suo valore massimo proprio in corrispondenza di tale valore medio:

• risulta essere unimodale, di conseguenza media, moda e mediana della distribuzione normale coincidono;

• è asintotica, tendente a 0, al tendere di x verso −∞ o +∞;

• il suo grafico presenta due punti di flesso in corrispondenza di x = μ – σ e x = μ + σ;

• il valore di tutta l’area sottesa dall’intera curva è uguale a 1 e le variazioni dalla forma caratteristica, a parità di valore medio, dipendono essenzialmente dal valore dello scarto quadratico medio.

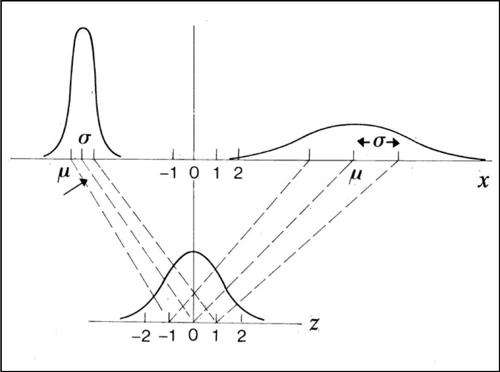
La probabilità che una variabile normale assuma un valore appartenente all’intervallo [x₁, x₂] è uguale all’area della regione racchiusa dalla curva, dall’asse delle ascisse e dalle rette di equazione X = x₁, e X = x₂. Le probabilità che tale variabile assuma valori in intervalli simmetrici rispetto alla media, espressi in termini di unità di scarto quadratico medio, sono costanti; per essi si veda → curva normale. Per calcolare la probabilità che la variabile aleatoria assuma valori compresi nell’intervallo [x₁, x₂], occorrerebbe, in generale, calcolare il suo integrale, ma esso non è facilmente calcolabile. Per tale motivo, si opera una trasformazione di tale distribuzione e se ne considera quindi una sua tabulazione. La trasformazione è la seguente:

La funzione di densità di Z è allora:

la cui distribuzione, detta distribuzione normale standardizzata, ha parametri μ = 0 e σ = 1. Così standardizzato, il grafico della funzione relativa è simmetrico rispetto all’asse delle ordinate, è crescente se e solo se z < 0, ha due flessi per z = ± 1 e interseca l’asse delle ordinate in

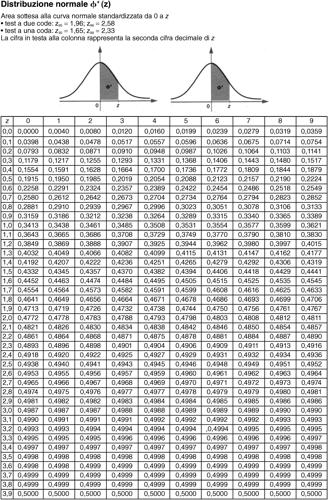
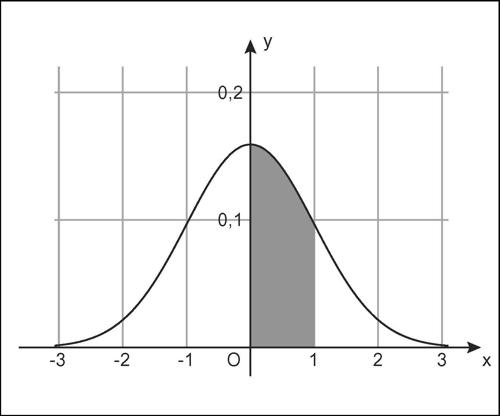
dove ha massimo assoluto. La probabilità che la variabile Z assuma valori nell’intervallo [z₁, z₂] è anche in questo caso data dall’area della regione sottesa alla curva in tale intervallo. Così P(0 ≤ 0 Z ≤ 1) è data dall’area della superficie sottesa al grafico nell’intervallo [0, 1]. L’area che fornisce le probabilità che Z sia minore o uguale a un determinato valore x è la funzione di ripartizione della variabile normale, è indicata con Φ(x) = P(Z ≤ x) ed è riportata in una apposita tavola della distribuzione normale (si veda la tavola relativa).