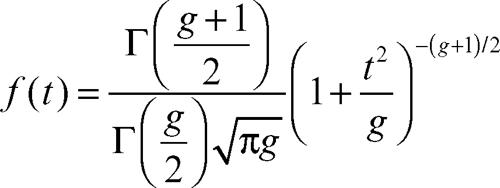Student, distribuzione t di
Student, distribuzione t di
Student, distribuzione t di distribuzione di probabilità di una variabile aleatoria continua, impiegata nell’inferenza statistica nel caso di campioni di ampiezza limitata. Fu introdotta dall’inglese W.S. Gosset, che pubblicò i suoi risultati nel 1908 con lo pseudonimo di Student. Una variabile aleatoria continua ha tale distribuzione, detta semplicemente t di Student, con g gradi di libertà, se la sua funzione di densità è:
con ‒∞ < t < +∞, in cui Γ è la funzione gamma di → Eulero. I valori della distribuzione si leggono dalla tavola e dipendono dal livello di significatività (α = 0,05 o α = 0,01) e dai gradi di libertà g, cioè dal numero di osservazioni indipendenti. Il suo valore medio e la sua varianza sono rispettivamente E(X) = 0 (per g > 1) e
All’aumentare di g la distribuzione di Student tende alla distribuzione normale standardizzata e già per g = 30 ne è una buona approssimazione; essa occupa un posto importante nell’inferenza statistica perché, quando il campione è piccolo (n < 30), approssima la distribuzione del carattere in esame meglio della distribuzione normale.
Dato un campione di ampiezza n estratto da una popolazione normale, con valore medio μ e varianza non nota, si dimostra che ha una distribuzione t con g = n − 1 gradi di libertà la quantità
dove x̄ e s sono la media e lo scarto quadrato medio del campione. Tale quantità può allora essere impiegata per la costruzione di intervalli di confidenza per μ, e per la verifica dell’ipotesi μ = x̄. La variabile t è anche impiegata per verificare l’ipotesi di uguaglianza tra i valori medi di due variabili normali X1 e X2 di uguale ma ignota varianza e per verificare l’ipotesi di indipendenza stocastica fra due variabili normali.
Si veda la tavola della distribuzione di Student.
t di Student per quantili: tab_lettS_08080_001.jpg>