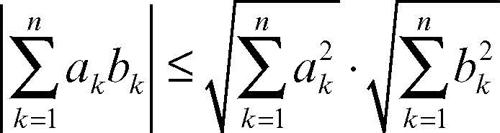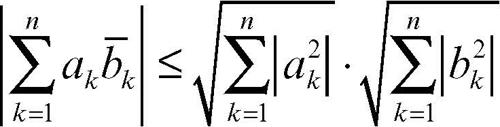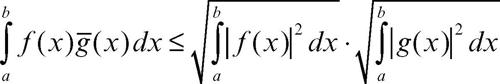Cauchy, disuguaglianza di
Enciclopedia della Matematica (2013)
Cauchy, disuguaglianza di
Cauchy, disuguaglianza di detta anche disuguaglianza di Cauchy-Schwarz, assume le forme:
(per n-ple di numeri reali (a1, …, an) e (b1, …, bn))
(per n-ple di numeri complessi)
e si interpreta introducendo il prodotto scalare (qui indicato come coppia di vettori in parentesi) e la norma euclidea, indicata con ‖…‖, tra i vettori x e y ∈ Rn (o Cn) come |(x, y)| ≤ ‖x‖ · ‖y‖.
La generalizzazione naturale allo spazio l 2 è
con {ak}, {bk} ∈ l 2, mentre in L2(a, b) assume la forma
con ƒ, g ∈ L2(a, b).