doppia implicazione
doppia implicazione
doppia implicazione o bicondizionale, connettivo logico denotato con il simbolo ⇔. Dati due enunciati A e B, l’enunciato A ⇔ B (si legge «A se e solo se B») si definisce come la congiunzione di due implicazioni; equivale cioè alla congiunzione dell’enunciato A ⇒ B e del suo inverso B ⇒ A, ovvero a (A ⇒ B) ∧ (B ⇒ A) o, in altri termini, alla coppia di affermazioni «da A discende B e da B discende A». Per esempio, si considerino le due proposizioni seguenti:
• P: «a è l’ipotenusa di un triangolo rettangolo e b, c sono i cateti».
• Q: «il quadrato costruito su a ha area uguale alla somma delle aree dei quadrati costruiti su b e su c». Per il teorema di Pitagora e il suo inverso, le due proposizioni precedenti sono equivalenti, cioè:
• P implica Q (in simboli P ⇒ Q) cioè «se a è l’ipotenusa di un triangolo rettangolo e b, c sono i cateti, allora l’area del quadrato costruito su a è la somma delle aree dei quadrati costruiti su b e su c»;
• Q implica P (in simboli Q ⇒P) cioè «se il quadrato costruito su a ha area uguale alla somma delle aree dei quadrati costruiti su b e su c allora a è l’ipotenusa di un triangolo rettangolo e b, c sono i cateti».
Queste due condizioni sono riassunte dall’unica formula P ⇔ Q che corrisponde alla proposizione «P se e solo se Q» (talvolta abbreviata nelle pubblicazioni specialistiche in lingua italiana con sse, in lingua inglese con iff).
A volte per tradurre la doppia implicazione fra due enunciati (A ⇔ B) si usa anche la dicitura «A è condizione necessaria e sufficiente per B»; in questa duplice espressione la parte «A è condizione necessaria per B» corrisponde all’implicazione (B ⇒ A) mentre la parte «A è condizione sufficiente per B» corrisponde all’implicazione (A ⇒ B).
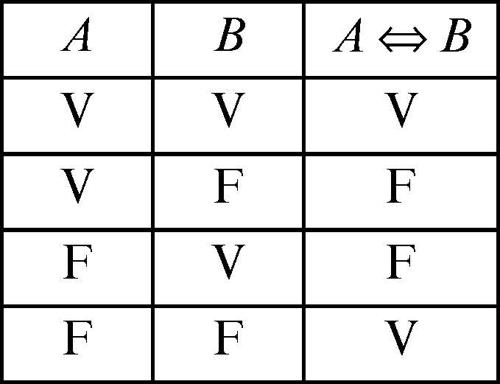
L’enunciato A ⇔ B è vero nel caso in cui A e B hanno lo stesso valore di verità, mentre è falso negli altri casi come espresso dalla sua tavola di verità: