dualita

dualita

dualità relazione tra due concetti, oggetti o strutture matematiche di una stessa teoria che sussiste se, scambiando il loro posto in uno o più assiomi o teoremi, si ottengono assiomi o teoremi ugualmente validi: i due oggetti matematici per cui vale una relazione di dualità si dicono allora duali. Per esempio, nel piano proiettivo sono duali i concetti di punto e retta perché come vale che «ogni coppia di punti distinti individua una e una sola retta», così vale che «ogni coppia di rette distinte individua uno e un sol punto». Proprio in tale contesto il termine fu introdotto dal francese J.-D. Gergonne che stabilì il principio generale, detto principio di dualità, secondo il quale ogni teorema nel piano riguardante punti e rette e che non coinvolge relazioni metriche corrisponde a un altro teorema in cui punti e rette sono tra loro scambiati.

In molti altri settori della matematica si trovano oggetti duali: a essi si può applicare, con le dovute cautele, un principio come il precedente che, per così dire, raddoppia l’ambito dei teoremi e delle procedure risolutive trovati permettendo che essi siano trasferiti da un oggetto al suo oggetto duale: per esempio, l’unione e l’intersezione nella teoria degli insiemi, problemi di massimo e minimo nella programmazione lineare, spazio vettoriale e relativo spazio vettoriale duale e, più in generale, lo spazio topologico duale.

La relazione di dualità è utilizzata in diversi ambiti della matematica, con significati specifici ulteriormente precisati.

☐ In geometria proiettiva, vale nel piano un principio di dualità che afferma che qualsiasi proposizione contenente punti e rette è equivalente alla proposizione che si ottiene scambiando tra loro le parole «punto» e «retta». Come nel caso sopra indicato della dualità tra i due assiomi di incidenza nel piano, nello spazio proiettivo tridimensionale sono duali i due assiomi: «tre punti distinti non appartenenti a una stessa retta individuano un piano» e «tre piani distinti non appartenenti a una stessa retta individuano un punto». Si noti che nei due assiomi le parole «punto» e «piano» risultano duali in quanto si scambiano tra loro passando da un assioma all’altro, mentre la parola «retta» si scambia con sé stessa e quindi la retta è un oggetto autoduale nello spazio proiettivo. Il principio di dualità vale in generale in uno spazio di dimensione n quando si scambiano tra loro due oggetti di dimensioni complementari rispetto a n. In base a tale principio, dato uno spazio di dimensione n, si può considerare il suo spazio duale costituito da tutti gli iperpiani dello spazio assegnato. Il principio vale in particolare per tutti gli assiomi e i teoremi e permette, una volta dimostrato un teorema, di non dimostrarne il teorema duale. Il principio di dualità non è un teorema della geometria, ma un teorema sulla geometria, cioè un metateorema (→ metamatematica). Un esempio di teoremi duali nel piano è costituito dal teorema di → Pascal e dal teorema di → Brianchon, mentre il teorema di → Desargues risulta autoduale.

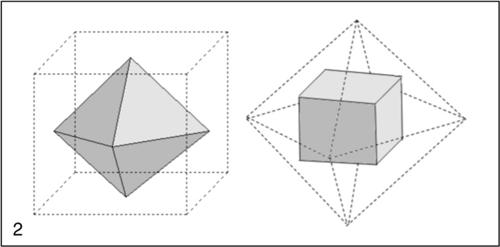
☐ Nello spazio ordinario tridimensionale il poliedro duale di un poliedro P è il poliedro P* ottenuto scambiando i ruoli dei vertici e delle facce di P. Il duale di P* è a sua volta P. Tra i solidi platonici il cubo e l’ottaedro risultano duali, così come risultano duali l’icosaedro e il dodecaedro, mentre il tetraedro è duale di sé stesso ed è detto pertanto autoduale.

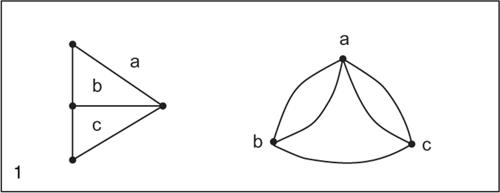
☐ Nella teoria dei grafi, dato un grafo G, il suo grafo duale G* si ottiene con la seguente procedura: ogni faccia di G, compresa la faccia infinita, è rappresentata in G* con un nodo e ogni arco di G che separa due regioni è rappresentato in G* da un arco che congiunge i corrispondenti nodi.

☐ In algebra lineare, lo spazio duale V* di uno spazio vettoriale V su un campo K, è lo spazio vettoriale i cui elementi sono i funzionali lineari su V (→ spazio duale).

☐ In topologia, si definisce → spazio topologico duale di uno spazio topologico X lo spazio vettoriale completo X′ (o X*) costituito dai funzionali lineari e continui su X.

☐ In analisi, lo spazio delle distribuzioni, intese come funzioni generalizzate, è definito come duale dello spazio delle funzioni test (→ distribuzione).

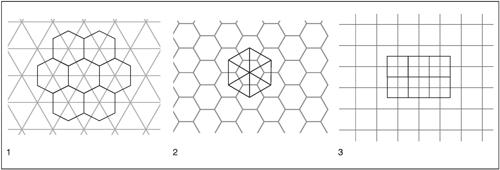
☐ Nei problemi di tassellazione del piano, in cui un ricoprimento del piano è ottenuto attraverso poligoni, la tassellazione duale si ottiene congiungendo i centri dei poligoni della data tassellazione. Così, una tassellazione del piano con triangoli equilateri ha per duale una tassellazione con esagoni e viceversa, mentre una tassellazione con quadrati è autoduale.