cubo, duplicazione del
cubo, duplicazione del
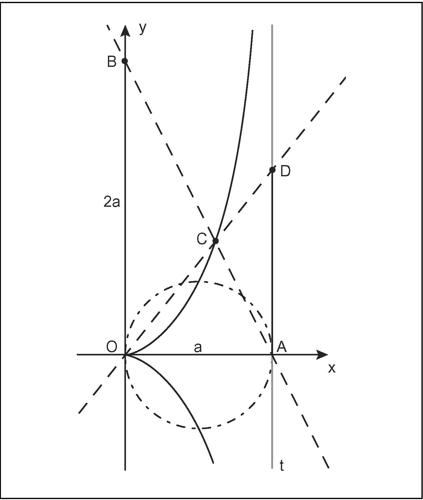
cubo, duplicazione del problema che consiste nel costruire, con riga e compasso, il lato di un cubo che abbia volume doppio a quello di un cubo dato, assegnato il suo spigolo. È detto anche problema di Delo perché Teone di Smirne narra che gli abitanti di Delo avevano domandato all’oracolo che cosa avrebbero dovuto fare per liberarsi dalla peste e questi aveva risposto che avrebbero dovuto costruire un altare ad Apollo di forma cubica, ma di volume doppio rispetto a quello esistente. Algebricamente, il problema è elementare perché, dato lo spigolo a, si tratta di trovare x tale che x 3 = 2a3 e pertanto
Tuttavia, non è possibile realizzare una tale costruzione con riga e compasso. Insieme a problemi quali quello della trisezione dell’→ angolo o della → quadratura del cerchio, la duplicazione del cubo è stata oggetto, per molti secoli, di faticosi tentativi di risoluzione, ma solo con la nascita dell’algebra moderna si è potuta dimostrare l’impossibilità della sua risoluzione con strumenti elementari. Esistono tuttavia, fin dal iv secolo a. C., numerosi esempi di soluzioni del problema della duplicazione del cubo ottenute con altri strumenti. Tra queste si può ricordare la soluzione di Ippocrate di Chio ottenuta mediante l’inserimento di due segmenti x e y, medi proporzionali tra a e 2a, cioè tali che risulti a : x = x : y = y : 2a, scrittura equivalente a x 3 = 2a3. La soluzione di Nicomede si serve della concoide, mentre la soluzione di Menecmo si basa sull’intersezione di due coniche. Infine la soluzione proposta da Diocle utilizza la cissoide nel modo che segue. Se {{{1}}}a è lo spigolo del cubo da duplicare, si costruisca la cissoide associata alla circonferenza di diametro OA, come nella figura, e si consideri il punto tale che BO = 2a. Indicato con C il punto di intersezione del segmento AB con la curva, sia D il punto in cui la retta per O e C interseca la tangente t alla circonferenza condotta per A. Il segmento AD è lo spigolo del cubo che duplica il cubo di spigolo OA.