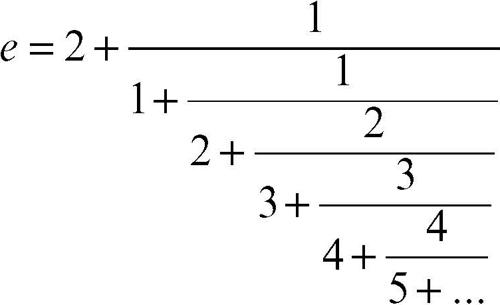e (numero di Nepero)
e (numero di Nepero)
e (numero di Nepero) simbolo del numero irrazionale trascendente base dei logaritmi naturali. Prende il nome dal matematico J. Napier (latinizzato in Nepero) vissuto tra xvi e xvii secolo e inventore dei logaritmi, ma la sua denominazione si deve a L. Eulero, vissuto più di un secolo dopo, che con tale lettera indicò la base dei logaritmi naturali. Il valore approssimato del numero e è 2,718281828459… Il numero e (decimale, illimitato non periodico) può essere calcolato in valore approssimato o mediante la somma della serie
(rappresentazione dovuta a I. Newton nel 1669) o come limite di successione:
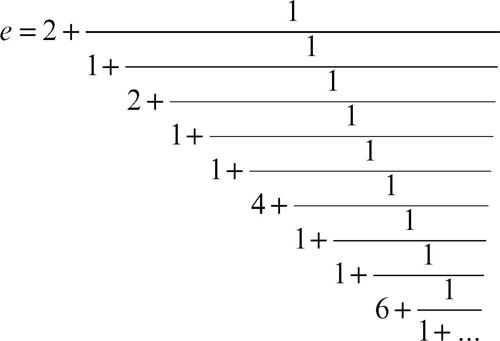
In realtà Nepero non scrisse mai questo limite (nel 1613 il concetto di limite non era stato ancora introdotto) e neppure trovò una approssimazione di e, ma i suoi logaritmi corrispondono a quelli scritti in tale base. Altre rappresentazioni del numero e sono date dalle frazioni continue:
ed
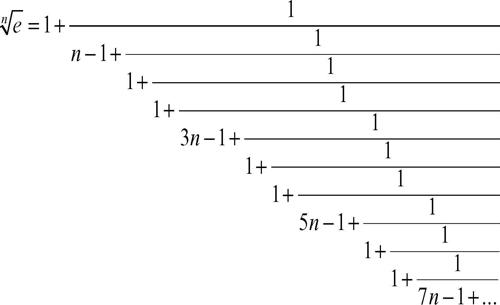
Interessante è pure lo sviluppo
L’irrazionalità di e fu provata da Eulero nel 1737, la sua trascendenza da Ch. Hermite nel 1873 (→ numero trascendente); la sua misura di irrazionalità è μ(e) = 2.
L’importanza per l’analisi matematica del numero e come base dei logaritmi discende dai numerosi limiti notevoli che a esso sono collegati. In particolare, la derivata della potenza di base a ed esponente x, y = ax, è y′ = axIna, per cui scegliendo e come base della potenza, il coefficiente Ine diventa uguale a 1 e si ha che la derivata di y = ex è y′ = ex così che tutte le formule conseguenti si semplificano. In particolare, con tale base assumono una scrittura più snella la funzione primitiva di 1/x, gli sviluppi di Maclaurin di ex e di ln(1 + x) (→ Maclaurin, serie di), le equazioni differenziali a coefficienti costanti e la formula di → Eulero nel campo complesso.
lettE_00030.rtf