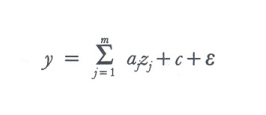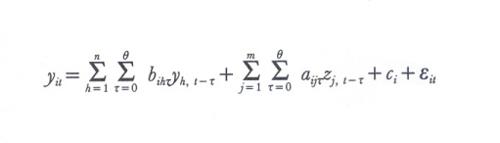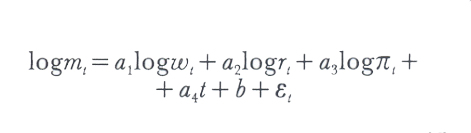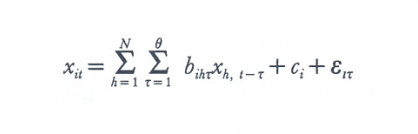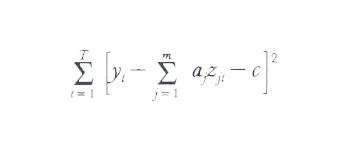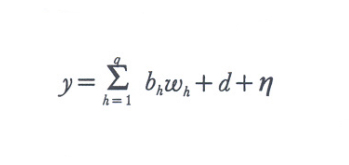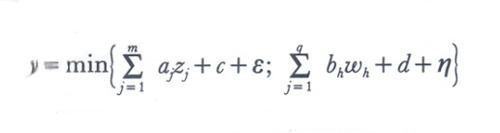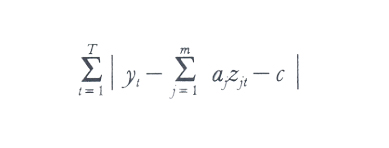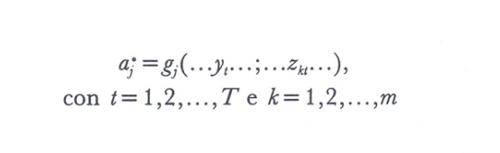Econometria

Econometria

Introduzione

L'econometria è oggi una branca della scienza economica; ma per conoscerla a fondo bisogna tener presente che a suo tempo essa fu anche un movimento che propugnava un nuovo orientamento di ricerca in economia e che attualmente essa costituisce anche una qualifica professionale. Il nome stesso, ancora poco usato all'inizio del secolo, cominciò a diffondersi dopo che nel 1930 fu creata l'Econometric Society (v. Christ, 1983). I suoi fondatori - alcuni studiosi europei e americani - intendevano promuovere l'uso di metodi quantitativi e matematici capaci di dare alla teoria economica il rigore, la precisione e l'oggettività che le mancavano e di renderla meglio utilizzabile da parte dei pubblici poteri. Il movimento, cui parteciparono attivamente alcuni futuri premi Nobel per l'economia, si sviluppò rapidamente, nonostante certe prevenzioni ideologiche sia di destra che di sinistra: se intorno al 1950 i partecipanti ai congressi europei della Società non erano più di qualche decina, verso il 1970 erano circa cinquecento. La rivista della Società, "Econometrica", fondata nel 1933, divenne nel dopoguerra una delle più prestigiose tra gli economisti di tutto il mondo.Quarant'anni fa il termine 'econometrista' indicava sia un economista matematico, sia un ricercatore che si dedicava a stimare delle relazioni o a verificare delle ipotesi mediante osservazioni statistiche; del resto le due qualifiche erano spesso associate nella stessa persona. Oggi la prima accezione è pressoché scomparsa: esercitano la professione di econometristi - nei centri di ricerca universitari, nelle amministrazioni pubbliche e nelle grandi aziende - coloro che si occupano dell'induzione statistica sui dati economici, o che lavorano su modelli quantitativi che riproducono fenomeni economici, ad esempio l'evoluzione macroeconomica di un paese.

In quanto disciplina, l'econometria è anzitutto un metodo per il trattamento induttivo delle osservazioni, analogo a quello adottato nelle scienze naturali per utilizzare i dati sperimentali. In secondo luogo è un complesso di tecniche elaborate per applicare tale metodo nel quadro di specificazioni che spesso sono peculiari dei fenomeni economici e a partire da dati non sperimentali. Infine è un complesso di risultati ottenuti per induzione come certe pratiche seguite per prevedere gli effetti di cambiamenti (subiti o voluti) del contesto in cui si svolge l'attività economica. Pertanto l'economia matematica, che si occupa di determinare per via deduttiva le proprietà dei modelli teorici usati dagli economisti, va considerata oggi al di fuori dell'econometria.

Il metodo

La scienza economica ha tardato a definire il proprio modo d'intendere il ruolo dell'osservazione nello studio dei fenomeni di sua competenza, l'apporto della raccolta sistematica di dati e i mezzi adeguati per utilizzare tale apporto. Per molto tempo gli economisti che intendevano fondare la conoscenza su basi empiriche hanno avuto una posizione secondaria. È solo verso la metà del nostro secolo che si è delineata una metodologia che associa i due procedimenti, deduttivo e induttivo; essa peraltro è ancora oggetto di discussioni riguardanti le sue modalità e talvolta addirittura i suoi stessi principî. Seguire l'evoluzione storica delle idee sull'econometria sarà utile per comprendere il metodo di questa disciplina.

Induzione e deduzione

All'inizio del XX secolo la filosofia della scienza aveva cercato di enucleare una struttura logica comune a tutte le teorie. Al centro di tale struttura vi era una legge che esprimeva la dipendenza di un risultato B da certi fattori esplicativi, rappresentati simbolicamente da A: ogni volta che A si verifica, si produce anche B. Occorreva quindi distinguere la verità delle condizioni A da quella della legge. Inoltre i logici usavano distinguere nelle leggi due categorie di proposizioni: le prime, dette 'analitiche', erano vere perché era possibile dimostrarle mediante una pura deduzione logica in base alle definizioni dei termini che vi figuravano; le altre, dette 'sintetiche', erano valide solo nel caso che fossero verificabili per induzione mediante un'esperienza pratica.Ma altri studiosi, opponendosi a coloro che sostenevano l'unità metodologica delle scienze, affermavano che per verificare la validità delle proprie leggi le scienze sociali seguivano vie diverse da quelle delle scienze naturali: nelle prime l'intuizione, l'introspezione, la conoscenza diretta dall''interno' dei fenomeni sostituivano l'osservazione dall'esterno del mondo della natura (v. Blaug, 1980, specialmente pp. 46 ss.).

Questa tesi era largamente adottata dalla maggioranza degli economisti: essa fu espressa chiaramente da L. Robbins (v., 1932) in una piccola opera molto diffusa, in cui veniva svolta l'idea secondo cui "in economia i costituenti primari delle generalizzazioni fondamentali ci sono noti in modo immediato", "la validità di una teoria particolare è una questione di dimostrazione logica a partire dalle ipotesi adottate" e quindi l'economia è una branca della logica, un modo di pensare.

Una tale concezione, di cui si avverte tuttora qualche eco, non era condivisa da una corrente minoritaria - formatasi già da tempo - che intendeva fondare la conoscenza economica sullo studio dei fatti osservati, ed era decisamente respinta dal giovane movimento econometrista, che, per di più, si proponeva di applicare ai fenomeni economici induzioni rigorose, condotte nel quadro di un modello aleatorio assunto come vero.Fino allora la necessità di un modello del genere non era stata molto sentita: ad esempio, non l'avevano avvertita gli economisti di Harvard o quelli del National Bureau of Economic Research di New York, impegnati nel prevedere l'evolversi della congiuntura mediante un esame continuo delle serie statistiche più significative (v. Burns e Mitchell, 1946). L'idea si affermò gradualmente nel corso delle discussioni metodologiche suscitate dai primi lavori sulla stima delle funzioni di domanda e di produzione, e trovò espressione in quello che fu chiamato allora "l'approccio probabilistico" (v. Haavelmo, 1944).

L'approccio probabilistico

Ogni induzione fondata su dati osservati deve condurre a una conclusione sulla validità di un'ipotesi o sulla misura di un parametro; a tale scopo occorre applicare una regola (o una tecnica) definita in precedenza. Ma l'adeguatezza di questa regola dipende dalla natura del fenomeno studiato e dalla relazione tra la genesi dei dati osservati e il fenomeno stesso. Per scegliere in modo rigoroso la regola da adottare e per determinare le proprietà dei risultati cui essa conduce bisogna dunque specificare ciò che già si conosce riguardo al fenomeno e alla genesi dei dati, ossia ciò che si sa prima di prendere in esame i dati su cui l'induzione dovrà fondarsi. Tale specificazione, espressa da un modello, si basa sia sui risultati di induzioni precedenti, sia sulle conoscenze derivanti dalla familiarità con l''interno' dei fenomeni. Essa non è mai così precisa da poter fare a meno di termini aleatori, la cui distribuzione è più o meno rigorosamente definita; essa implica inoltre dei parametri, cioè degli elementi incogniti su cui l'induzione potrà esercitarsi. La definizione del modello aleatorio è quindi la premessa indispensabile per l'utilizzazione induttiva dei dati.

Di per sé questa concezione non è peculiare dell'econometria, ma si è imposta in tutti i campi d'applicazione della statistica allorché si è cercato d'introdurvi dei procedimenti rigorosi; tuttavia la sua applicazione ai fenomeni economici presenta alcune particolarità. Da un lato, salvo rarissime eccezioni, i dati economici non provengono da esperimenti scientifici, ma dalla semplice osservazione di una realtà influenzata da molteplici fattori; il modello dovrebbe identificarli tutti e rappresentarli correttamente. D'altro lato è difficile in genere isolare i fenomeni economici tra loro e da altri fenomeni di carattere sociale o politico, e anche per questa ragione risulta spesso necessario introdurre nel modello numerose variabili.

Consideriamo dunque il modello formale della regressione multipla, utilizzato in numerose discipline scientifiche, per vedere quale tipo di giustificazione l'econometrista gli attribuisce quando lo adopera. Data la relazione

[1] formula

si suppone che le variabili y e zj (j=1,2,...,m) siano osservabili senza errore, mentre la variabile ε è aleatoria e non osservabile direttamente; i coefficienti aj e la costante c sono dei parametri. Il modello specifica inoltre che la legge di probabilità di ε ha valore medio nullo e varianza σ², senza peraltro imporre alcuna restrizione alle aj, a c e a σ². Il modello rappresenta quindi la determinazione della grandezza y, detta endogena, a partire dalle grandezze osservabili zj, dette esogene, e da un insieme di cause non osservabili o non identificate, il cui effetto globale è rappresentato dalla variabile aleatoria ε, detta errore o perturbazione.

Si dispone di osservazioni sui valori assunti simultaneamente dalla y e dalle zj sia su diverse unità (sezione istantanea o cross section), sia in diversi periodi (serie temporali): indicheremo con yt e zjt questi valori (t=1,2,...,T). Il modello della regressione, in cui le aj, c e σ² conservano gli stessi valori in tutte le osservazioni, specifica inoltre che i valori εt della variabile aleatoria sono indipendenti tra loro.

Naturalmente il modello suddetto è solo uno fra i molti usati in econometria: si può avere una pluralità di variabili endogene considerate determinate simultaneamente; spesso la relazione o le relazioni che esprimono la determinazione sono non lineari e di varia forma; il valore assunto da una grandezza in un periodo può essere influenzato dai valori assunti in precedenza dalla grandezza stessa o da altre variabili; la o le variabili aleatorie non osservabili possono intervenire in maniera non additiva; le osservazioni, e quindi i corrispondenti errori εt, possono non essere indipendenti tra loro, ecc.L'esempio fornito già basta a illustrare la natura dei modelli tramite i quali l'approccio probabilistico trova applicazione in econometria; tuttavia in seguito sarà utile far riferimento anche a un altro modello, che ha svolto un ruolo importante nello sviluppo di questa disciplina (v. Koopmans, 1950; v. Hood e Koopmans, 1953). Esso tiene conto di due aspetti frequenti dei fenomeni economici: le interdipendenze tra grandezze e i ritardi con cui le grandezze interagiscono tra loro. Mantenendo la forma lineare della (1), il modello in questione si esprime con un sistema di n equazioni (i=1,2,...,n):

[2] formula.

Il massimo ritardo θ è fisso; i coefficienti bii₀ sono nulli per ipotesi, così come sono nulli alcuni dei coefficienti bihτ e aijτ: si considera infatti l'equazione (2) come esprimente la determinazione diretta della grandezza yi, ad esempio come risultato del comportamento di una pluralità di agenti, ed è noto che alcune grandezze esogene o endogene non intervengono in questa determinazione, o non vi intervengono con il ritardo τ.

Il modello dell'econometrista e quello dell'economista

Nonostante le varie possibilità sopra citate, di rado l'economista dispone di giustificazioni rigorose per considerare vero un modello aleatorio completamente specificato, o anche per supporre di primo acchito che un tale modello fornisca una sufficiente approssimazione alla realtà.Si pensi ad esempio a una legge di comportamento rappresentante la domanda di moneta in un paese. L'econometrista incaricato di analizzare delle serie temporali aggregate può aver impostato il seguente modello:

[3] formula

in cui mt è il rapporto tra la massa monetaria e il reddito nazionale espressi in valore, wt il rapporto tra la ricchezza nazionale e il reddito nazionale, rt un tasso d'interesse rappresentativo, πt il tasso d'aumento dei prezzi e t il tempo. L'econometrista può addurre a giustificazione del suo modello alcuni fatti: la detenzione di moneta è motivata da un insieme di esigenze di transazione, di precauzione o di risparmio legate al reddito e alla ricchezza dei detentori; d'altra parte costoro sono influenzati anche dal rendimento offerto da impieghi finanziari o reali di minore liquidità; infine il bisogno di moneta varia nel tempo in seguito ai mutamenti nelle modalità di pagamento e nella gamma degli strumenti finanziari offerti agli investitori.

Nell'analisi dei comportamenti individuali la teoria economica è in accordo con la rappresentazione adottata dall'econometrista; ma essa deve far intervenire un certo numero di ipotesi che non sono mai del tutto realistiche. L'aggregazione, cioè la costruzione di grandezze globali attribuibili a una collettività, ottenute sommando grandezze individuali, presuppone che siano verificate alcune condizioni piuttosto restrittive. Soprattutto i risultati teorici non stabiliscono né che il secondo membro dell'equazione (3) debba avere la forma adottata, né che le perturbazioni aleatorie successive εt siano indipendenti tra loro e abbiano la stessa varianza. L'econometrista deve quindi ricorrere ad altri due tipi di considerazioni.

Egli è consapevole che quanto potrà essere stabilito, tenuto conto di ciò che già si sa e di ciò che i dati disponibili consentiranno di trovare, sarà necessariamente frutto di una semplificazione. Del resto egli sarà spesso costretto a rinunziare alle ambizioni della prima specificazione considerata e ad accontentarsi - per giungere a una caratterizzazione precisa - di una relazione ancora più semplice dell'equazione (3). Ad esempio, se nelle serie utilizzate vi è una forte correlazione tra due variabili esplicative, il tempo t e il rapporto wt (si dice allora che queste variabili sono collineari), risulterà impossibile stimare con una certa precisione a_₁ e a_₄. L'econometrista potrà allora decidere di eliminare dalla relazione da stimare il termine di tendenza a₄t, il che gli consentirà di valutare in maniera apparentemente precisa il coefficiente a₁, sia pure col rischio di un 'errore di specificazione' (sulla possibilità che un simile rischio si avveri v. Poole, 1988).

La giustificazione delle procedure correnti si basa quindi - che se ne sia consapevoli o meno - anche su un altro ordine di considerazioni: quelle che riguardano la necessità di adottare convenzioni di lavoro che consentano di organizzare lo sforzo collettivo degli econometristi. Il modello aleatorio dà ai procedimenti econometrici impiegati un significato che sarebbe chiaro se si fosse certi che il modello è assolutamente realistico; in pratica le incertezze relative al modello fanno sì che quel significato sia meno chiaro, anche se esso non viene a mancare, in quanto il riferimento al modello dà trasparenza al lavoro compiuto. La trasmissione delle conoscenze empiriche tra gli economisti utilizza infatti come veicolo non solo le valutazioni numeriche di coefficienti come quelli presenti nell'equazione (3), ma anche i modelli adottati per ottenerle: salvo motivi particolari, l'econometrista si attiene dunque a una specificazione che risulta familiare a coloro ai quali si rivolge. Il modello, i risultati e le relative proprietà hanno perciò un carattere alquanto convenzionale.

La corrente bayesiana

In pratica il modello non esprime esattamente le conoscenze oggettive preesistenti all'esame dei dati che l'econometrista deve utilizzare. Da un lato esso è più preciso di queste conoscenze, per le grandezze che prende in considerazione e per quelle che esclude, per la forma della relazione che esprime, per il modo in cui introduce i termini aleatori, per le ipotesi che adotta circa la legge di probabilità di questi ultimi, ecc. D'altro lato il modello è di solito troppo impreciso circa i valori dei parametri che fa intervenire: può darsi che si sappia che certi valori non appartengono all'insieme dei valori economicamente accettabili, può darsi che la stima dei parametri sia stata fatta in altri luoghi o in altri periodi, che non sembrano dover produrre effetti sostanzialmente diversi, ecc. In realtà specificare il modello aleatorio obbliga a una distinzione dicotomica tra noto e ignoto, che il più delle volte è artificiosa rispetto al grado variabile d'incertezza delle conoscenze disponibili. Anziché costringersi a specificare un modello che renda in termini distorti la situazione, sarebbe meglio, logicamente, esprimere le conoscenze preventive con delle probabilità.

Questa difficoltà non è peculiare dell'econometria, e già da tempo vi è una corrente della metodologia statistica che offre una soluzione del problema, ponendolo nei termini seguenti. Prima dell'esame di un nuovo campione di dati osservati conviene specificare la legge di probabilità che esprime lo stato delle conoscenze sul fenomeno in questione ('legge a priori'); i nuovi dati portano a una revisione delle conoscenze, che vengono ora espresse da un'altra legge di probabilità, detta 'legge a posteriori'. L'induzione va intesa come l'operazione di passaggio dalla prima alla seconda legge; le regole da seguire a tale scopo sono definite dal calcolo delle probabilità, mediante l'applicazione del 'teorema di Bayes'. La scuola bayesiana si è dedicata ad approfondire sia la logica induttiva così concepita (v. Savage, 1954; v. De Finetti, 1970), sia i procedimenti che permettono di utilizzarla in alcune specificazioni correnti (v. Zellner, 1971).

In linea di principio questo modo d'impostare il problema è del tutto convincente, ma la sua attuazione complica i procedimenti da seguire e obbliga a compiere scelte convenzionali ancora più numerose di quelle necessarie per l'applicazione dei procedimenti classici; l'approccio bayesiano è quindi più utile nello stadio della riflessione di base che non nel lavoro corrente degli econometristi.

Va notato anzitutto che rimane necessario un modello aleatorio che descriva la genesi delle osservazioni. Stando all'impostazione bayesiana, il modello dovrebbe essere molto meno speciale di quelli presi abitualmente in considerazione in econometria; ma in pratica i procedimenti richiesti sono stati definiti solo per i modelli usuali, ad esempio per quello della regressione multipla.

La definizione della legge a priori presenta una duplice difficoltà. Da un lato riconoscere che esiste una certa conoscenza preventiva non vuol dire che si possa esprimere agevolmente la sua natura e il suo grado di certezza; d'altro lato, per poter essere utilizzata nel lavoro collettivo di ricerca, questa conoscenza dovrebbe essere oggettiva, cioè riconosciuta valida da tutti, mentre le nozioni preliminari sono spesso alquanto soggettive. Ciò fa sì che le sole soluzioni possibili siano relativamente convenzionali. I risultati ottenuti con i procedimenti bayesiani finiscono quindi con l'essere simili a quelli ricavati con i procedimenti classici.

Il ruolo dell'analisi dei dati

L'approccio probabilistico si era imposto senza rivali in econometria, sia nell'insegnamento che nella ricerca, quando, una ventina di anni fa, è ricomparsa l'idea secondo cui nell'esaminare un insieme di dati conviene spesso astrarre da ogni nozione preliminare. Con l'espressione 'analisi dei dati' oggi si indica un complesso di tecniche il cui impiego non presuppone la specificazione di un vero e proprio modello riassuntivo delle conoscenze preesistenti. Il ritorno a quest'idea si spiega in parte col carattere troppo dogmatico con cui spesso si è presentato, specialmente sul finire degli anni quaranta, l'approccio probabilistico.

Per cogliere bene non solo il contesto di quell'epoca, ma anche la vera posta in gioco in alcune discussioni più recenti, è opportuno richiamarsi al dibattito metodologico suscitato dalla pubblicazione di un'opera di Burns e Mitchell (v., 1946). In un lungo articolo Koopmans (v., 1947) criticò il metodo empirico adottato nell'opera, che secondo lui apparteneva alla "fase di Keplero", e sostenne invece l'approccio probabilistico, che rifletteva il passaggio alla "fase di Newton". Due anni dopo quest'articolo diede origine a un lungo scambio di opinioni tra Koopmans e R. Vining, che difendeva il lavoro svolto presso il National Bureau of Economic Research.

La parte più interessante di questo dibattito emerge dalle due citazioni che seguono. Dopo aver rimproverato a Koopmans di aver falsato le reali intenzioni di Burns e Mitchell, in modo da spostare la propria critica su un terreno favorevole, Vining afferma che l'opera dei due studiosi si propone uno studio esplorativo delle fluttuazioni economiche, che le conoscenze fattuali sistematiche sono rare e che sarebbe più importante per gli economisti concentrare l'attenzione sul problema primario di "ricercare le regolarità e le concordanze o le discordanze esistenti tra esse, e identificare gli eventuali modelli interessanti", anziché precipitarsi ad affrontare problemi successivi di test e di stima. Nella sua replica Koopmans non rinunzia alla sua argomentazione principale, ma verso la fine riconosce che "resta un margine di dubbio sul fatto che tutta l'attività di ricerca di ipotesi valide possa essere descritta e formalizzata come una scelta nell'ambito di un elenco prestabilito di alternative". Tuttavia questo vago dubbio non riscosse allora molta attenzione da parte degli econometristi.

Una reazione contro i principî classici dell'induzione si è manifestata del resto nella stessa statistica matematica. Pur senza mettere in discussione l'uso di questi principî quando si tratta effettivamente di eseguire test o stime, alcuni statistici hanno rivolto la propria attenzione a procedimenti di calcolo e di rappresentazione che tendono a essere puramente descrittivi, visto che il complesso dei dati da considerare appare spesso indecifrabile, a meno che non venga rielaborato e condensato (v. Benzécri, 1973; v. Tukey, 1977).

L'interesse per la statistica descrittiva, che è sempre stato prevalente tra gli studiosi della congiuntura, si è risvegliato da più di un decennio anche in alcuni econometristi, sensibili al fatto che i modelli aleatori abitualmente adottati perdono di valore in quanto sono convenzionali o in quanto derivano (senza che lo si dica) da un primo esame dei dati (v. Leamer, 1978).

Con la stessa considerazione si spiega come si sia fatta strada l'idea di utilizzare per l'analisi dei dati temporali un procedimento induttivo fondato su un modello che, pur essendo aleatorio, sia poco vincolante e non pretenda di rappresentare i comportamenti economici. Coloro che propongono questo procedimento ritengono che la teoria economica non offra una guida abbastanza affidabile da far sì che si debbano adottare le forme particolari che ad essa si ispirano. Questi studiosi criticano ad esempio i modelli a equazioni simultanee, come quelli rappresentati dal sistema (2), e la presunta nullità di molti dei coefficienti bihτ e aij⟨FT₁₀₅>t: secondo loro questa nullità manca di fondamento, e ciò li induce a negare la validità dei risultati basati su di essa. Preferiscono quindi ignorare a priori la teoria economica e condurre le loro indagini nel quadro di modelli descrittivi il più possibile neutri, salvo 'riscoprire' la teoria nel momento di interpretare i risultati (v. Sims, 1980).

Nelle 'autoregressioni vettoriali' calcolate con questo procedimento alternativo non si fa più distinzione fra grandezze endogene ed esogene: tutte le variabili xi (i=1,2,...,N) sono trattate nella stessa maniera. Nel modello seguente il valore assunto da ciascuna variabile nel periodo t è espresso come funzione lineare dei valori assunti anteriormente da tutte le variabili, fino a un ritardo massimo θ:

[4] formula.

Nessuno dei coefficienti bihτ è considerato noto a priori.

Tali autoregressioni vettoriali hanno oggi un ruolo descrittivo interessante, specialmente nello studio dei dati macroeconomici, ma non possono sostituire in generale i procedimenti econometrici più classici. Come le altre tecniche di analisi dei dati, esse trascurano tutte le conoscenze preventive disponibili sui fenomeni da esaminare; ma allora i dati risultano il più delle volte troppo poveri perché le autoregressioni portino a conclusioni sufficientemente significative.

Le tecniche

Se oggi l'econometria è una vera e propria professione, ciò è dovuto al fatto che in essa viene utilizzato consapevolmente e con competenza un complesso di tecniche, ciascuna delle quali è adatta a un dato oggetto e a un dato contesto. Le proprietà di queste tecniche sono per lo più ben note; in particolare è noto il grado di affidabilità dei risultati che esse forniscono. La professione si è costituita a poco a poco, man mano che l'interesse si andava spostando da certi obiettivi ad altri e da certi contesti di problemi ad altri. I principî del procedimento da seguire rimanevano essenzialmente gli stessi, ma bisognava saperli adattare efficacemente a ciascun caso. La professione di econometrista s'insegna grazie a numerose opere (ad esempio: v. Malinvaud, 1964; v. Anderson, 1971; v. Theil, 1971; v. Gouriéroux e Monfort, 1983; v. Gouriéroux, 1984; v. Griliches e Intriligator, 1983-1986).

Varietà di obiettivi e di procedimenti

La prima operazione da eseguire consiste nello stimare l'importanza di un dato effetto: l'elasticità di un consumo rispetto al prezzo o al reddito, la derivata della funzione che lega tra loro due aggregati, ecc. In un primo momento si è ritenuto che quest'operazione dovesse avvenire nel contesto di relazioni funzionali semplici alle quali si poteva dare una forma lineare, ossia nel contesto del modello di regressione (1). In tal caso si tratta di determinare i valori da attribuire ai coefficienti aj e alla costante c, utilizzando a questo scopo T osservazioni delle variabili yt e zjt (t=1,2,...,T; σ=1,2,...,μ). La tecnica più semplice consiste nel calcolare la regressione, ossia nell'adottare gli m+1 valori a*₁,...,a*m, c* che insieme rendono minima la somma dei quadrati degli scarti tra yt e la forma lineare delle zjt,

[5] formula,

trattando questa espressione come una funzione dei parametri da stimare a₁,...,am, c. Si dice anche che questa tecnica consiste nel calcolare il cosiddetto 'stimatore dei minimi quadrati'. Ma il caso appena presentato non esaurisce la molteplicità degli obiettivi e dei procedimenti degli econometristi, che si articolano sulle tre dimensioni seguenti.

1. In primo luogo non sempre si tratta di eseguire stime, ma spesso di raggiungere anche altri obiettivi. Il più frequente di essi, dopo la stima, consiste nel controllare se una relazione tra grandezze presenti una particolare proprietà. Ad esempio, una proprietà del genere potrebbe specificare che nella determinazione di y non deve intervenire z₁; se si è adottato il modello (1), ciò equivale a dire che il coefficiente a₁ è nullo. Si tratta allora di sapere se in base alle osservazioni yt e zjt si debba accettare o rifiutare questa proprietà. Un caso interessante di controllo riguarda la causalità: è possibile affermare che le variazioni della grandezza x₁ causano quelle della grandezza x₂? La questione, che evidentemente si pone spesso in economia, dà origine a un problema epistemologico che non sarà trattato in questa sede. Del resto gli econometristi ne sono consapevoli, visto che si limitano a verificare la 'causalità alla Granger', ossia l'anteriorità temporale delle variazioni di x₁ rispetto alle corrispondenti variazioni di x₂ (v. Granger, 1969). Orbene l'anteriorità temporale non è né necessaria né sufficiente per l'anteriorità logica (quest'ultima può essere istantanea; le variazioni di x₁ e di x₂ possono essere causate da una terza grandezza, x₃, che agisce su x₁ più rapidamente che su x₂).

Può anche trattarsi non di stimare o di controllare, ma di scegliere: ad esempio ci si può chiedere quale di due relazioni funzionali debba applicarsi nella determinazione di una grandezza y, se cioè si debba adottare la (1) oppure la

[6] formula,

le cui variabili esogene wh possono peraltro coincidere in parte con le variabili zj. Può trattarsi infine di prevedere (si dice anche 'proiettare') l'evoluzione futura di una grandezza. Ad esempio, quando si adotta il modello (1) e si sono osservati i valori yt e zjt per i periodi t=1,2,...,T, si può voler prevedere il valore yT+₁. La regressione risulta utile se si è in grado di stabilire per altra via le previsioni zj,T+₁ delle variabili esogene.

2. In secondo luogo le relazioni tra le grandezze osservate prese in considerazione possono avere forme molto varie, più o meno differenti da quella dell'equazione (1). L'importanza che le interdipendenze tra grandezze e i ritardi hanno in economia giustifica il ruolo del tutto particolare che i modelli dinamici a equazioni simultanee del tipo (2) hanno avuto nell'elaborazione delle tecniche econometriche (v. Koopmans, 1950). Per di più spesso nelle applicazioni i modelli sono non lineari; un esempio fra tanti è quello dei modelli a due regimi, che intervengono nello studio dei mercati dove lo scambio è determinato sia dalla domanda che dall'offerta:

[7] formula.

3. In terzo luogo, date la natura della questione da trattare e la forma della dipendenza tra le grandezze, le formule da usare possono ancora essere diverse. Così, per stimare i coefficienti aj e c della relazione (1), si utilizzano talvolta stimatori diversi dalle aj* e dalla c* - che nel loro insieme rendono minimo il valore della (5) -, ad esempio le âj e la ^c - che rendono minima la somma dei valori assoluti degli scarti:

[8] formula.

Proprietà dei procedimenti

Lo studio dei metodi econometrici è riconducibile a quello delle proprietà di vari procedimenti concepiti per risolvere differenti problemi nel quadro di diversi modelli aleatori. Ci limiteremo qui a riferirci alla stima dei coefficienti del modello di regressione (1); questo caso, sebbene molto semplice rispetto ad altri, mostra già come possono essere caratterizzate le proprietà dei procedimenti.

Un metodo di stima dei coefficienti aj e della costante c permette di calcolare dei valori di questi parametri in funzione delle sole osservazioni. Un metodo si traduce dunque nella definizione di un insieme di funzioni del tipo

[9] formula.

La funzione gj è detta 'stimatore' del coefficiente aj; nei manuali è indicato il modo di esprimere questa funzione, ad esempio quando si sia scelto di rendere minima la somma dei quadrati degli scarti (5).

Si pone naturalmente la questione di sapere con quale precisione uno stimatore si approssimi al valore vero del parametro cui si riferisce; ciò è utile sia per scegliere tra due o più stimatori, ad esempio tra quello che minimizza la (5) e quello che minimizza la (8), sia per utilizzare il risultato fornito da un determinato stimatore. La questione si risolve facilmente quando ci si riferisce al modello aleatorio. Il modello (1) specifica infatti la presenza, accanto alle variabili zj, di un errore aleatorio ε nella determinazione della grandezza endogena y. Prima delle osservazioni questa grandezza appare dunque aleatoria, mentre le zj possono essere trattate come certe, essendo ciò conveniente per rispondere alla maggior parte dei quesiti che ci si pone. Analogamente, prima delle osservazioni, i T valori yt, e quindi anche il valore aj* fornito dalla (9), appaiono aleatori. L'osservazione e il calcolo portano a un valore ben determinato di aj*, la cui precisione non può essere nota perché si ignora il valore vero aj. In compenso il modello permette di studiare la legge di probabilità dell'errore di stima aj*-aj, ossia di caratterizzare le proprietà aleatorie della stima. Se questa legge di probabilità è molto concentrata intorno allo zero, si ha la quasi certezza che l'errore aj*-aj è lieve; nel caso contrario si dovrà temere una notevole imprecisione della stima.

Le proprietà aleatorie di aj*- aj dipendono in primo luogo da quelle degli errori εt, poi dal complesso dei valori delle zjt, infine dai valori dei parametri, specialmente dal numero di osservazioni; tuttavia esse sono abbastanza note da parecchio tempo. Ad esempio, quando è possibile ammettere che gli errori εt sono indipendenti tra loro e dalle zjt e seguono tutti una stessa legge normale con media nulla, si sa che anche aj*-aj segue una legge normale dello stesso genere, il cui scarto quadratico medio σj dipende dalle zjt e dalla varianza σ² degli εt secondo una formula nota. Allora la stima non comporta distorsione, e la sua precisione è buona se σj è piccolo. Si conoscerebbe esattamente la distribuzione dell'errore di stima se si conoscesse in anticipo σ²; di solito ciò non accade, ma esiste uno stimatore non distorto di σ² che permette non solo di avere un buono stimatore σj* di σj, ma anche di calcolare il rapporto (aj*- aj)/Ϛj*, la cui legge di probabilità ('legge di Student') è perfettamente nota.

Tuttavia il più delle volte le proprietà sono meno forti. Se ad esempio si adottano tutte le ipotesi fatte finora sugli errori εt, tranne quella che la loro distribuzione sia normale, si può concludere che aj*-aj ha media nulla e che σj* fornisce un buono stimatore del suo scarto quadratico medio, ma non che la sua distribuzione di probabilità sia esattamente normale. Lo è però approssimativamente, nel senso che la legge di (aj*-aj)/σj* tenderebbe verso una legge normale se si ripetesse indefinitamente il calcolo su campioni di dimensione T crescente oltre ogni limite. Beninteso quest'ultima operazione è puramente virtuale, ma la 'proprietà asintotica' che si enuncia quando s'immagina di eseguirla è significativa, perché l'approssimazione normale è buona quando T non è troppo piccola.

Quest'ultimo caso tanto più merita di essere preso in considerazione in quanto la maggior parte delle proprietà enunciate dalla teoria econometrica ha lo stesso carattere asintotico. Ciò non sorprende, perché la complessità delle situazioni considerate e dei procedimenti disponibili per studiarle rende spesso impossibile la determinazione esatta delle leggi di probabilità. Non essendo però le giustificazioni asintotiche completamente probanti, è logico che la teoria econometrica si preoccupi anche di studiare, con indagini sia matematiche che empiriche, il grado delle approssimazioni che le riguardano.

Da un lato fra le proprietà asintotiche ve ne sono di più o meno forti, nel senso che la tendenza da esse indicata è più o meno rapida, e quindi l'approssimazione è più o meno stretta; i teorici vanno allora alla ricerca di proprietà forti, che portino ad approssimazioni aventi le migliori possibilità di essere buone anche con un piccolo numero di osservazioni.

D'altro lato, per studiare la qualità delle approssimazioni, gli specialisti di econometria possono eseguire esperimenti artificiali ('metodo di Montecarlo'), simulando i risultati di campioni rispondenti a un modello ben definito. È sufficiente per questo costruire artificialmente un gran numero di tali campioni e calcolare le stime alle quali ciascuno di essi porterebbe; per ogni parametro e per ogni tecnica di stima si disporrà allora di tante stime quanti sono i campioni, e la legge di probabilità dello stimatore in esame si manifesterà sperimentalmente attraverso la distribuzione statistica dei valori ottenuti.

Poiché la specificazione dei modelli utilizzati dagli econometristi è di rado precisa e ha in genere, come si è visto, un carattere piuttosto convenzionale, si annette un particolare interesse ai procedimenti 'robusti', cioè a quelli le cui proprietà principali sono indipendenti dalle particolarità della specificazione, o almeno ne dipendono in misura limitata; la teoria econometrica è portata quindi a studiare in modo sistematico questa 'robustezza'.

c) Serie temporali, sezioni istantanee, panel

Tenuto conto di quanto si è detto sulla varietà degli obiettivi e dei procedimenti, si può avere un'idea della molteplicità delle proprietà teoriche da esaminare e della vastità della corrispondente letteratura scientifica. Inoltre in ciò che precede non si è attribuita sufficiente importanza al tipo di dati di cui gli econometristi possono disporre. Questi dati possono essere di natura molto varia, ma si è soliti concentrare l'attenzione su due tipi: il ricorso all'uno o all'altro di essi influisce sulla scelta del modello, che dovrebbe esprimere nel miglior modo possibile la genesi dei dati.

Con le serie temporali si dispone di osservazioni sui valori assunti simultaneamente durante una successione di periodi t dalle diverse variabili, ad esempio dalle yit e zjt che compaiono nel modello (2). L'uso di questo tipo di dati, prevalente nell'analisi dei fenomeni macroeconomici, obbliga il più delle volte a prestare particolare attenzione, nella specificazione, non solo ai ritardi con cui gli effetti si fanno sentire, ma anche agli influssi stagionali o ai trends, che possono influire in modo diverso sulle varie grandezze. Inoltre è raro che nelle indagini econometriche gli errori εit di due periodi successivi si possano considerare indipendenti tra loro, il che introduce nuove complicazioni. Infine, poiché le serie temporali economiche sono relativamente brevi, i risultati sono sensibili all'eventuale decisione di escludere le osservazioni relative a uno o due periodi che si ritengono influenzati da avvenimenti eccezionali, estranei al fenomeno studiato.

Con le sezioni istantanee (cross sections) si dispone di osservazioni sui valori assunti in un dato periodo da diverse variabili relative a numerose unità (individui, famiglie, imprese, ecc.). La dimensione del campione è di solito molto più grande di quella fornita dalle serie temporali; tuttavia non si deve pensare che la precisione dei risultati econometrici sia sempre maggiore, perché non si tratta di dati sperimentali, per i quali si siano mantenute fisse tutte le grandezze diverse da quelle di cui interessano le variazioni, bensì di semplici osservazioni su unità influenzate da molteplici fattori e soggette a particolarità che non è facile identificare esattamente.

Oggi gli economisti dispongono sempre più spesso di dati relativi a panel, ossia a campioni nei quali le stesse unità sono osservate individualmente in una successione di periodi. Questi dati, in cui sono associate le due dimensioni delle serie temporali e delle sezioni istantanee, offrono ampie possibilità, ma obbligano anche a introdurre modelli piuttosto complessi e a ricorrere a tecniche opportunamente modificate (v. "Annales de l'INSEE", 1978).

I risultati

L'economia, in quanto scienza d'osservazione e di riflessione deduttiva, può progredire realmente solo se i risultati dell'induzione econometrica trovano reciproca conferma, dando origine nel loro complesso a un'acquisizione cumulativa di conoscenze. Viste in prospettiva, le ricerche del nostro secolo corrispondono bene a questo ideale; ma il progresso è molto più lento di quanto si sarebbe potuto sperare data la mole di lavoro svolto (circa metà degli articoli pubblicati oggi nelle riviste specializzate di economia contengono risultati econometrici originali). Si tratta inoltre di un progresso laborioso, perché da un lato numerose indagini econometriche portano a risultati deludenti per la loro imprecisione e dall'altro non vi è accordo fra i ricercatori sull'esistenza o sull'intensità di certi effetti capaci di esercitare un ruolo importante.Questa difficoltà non può sorprendere, considerando la complessità dei fenomeni economici, la frequenza dei mutamenti cui è soggetto il loro ambiente e l'impossibilità di eseguire esperimenti; d'altra parte tutto ciò influisce in modo diverso sulle varie questioni da chiarire: alcune possono essere isolate abbastanza bene, mentre altre si rivelano ardue già nella fase della loro formulazione. Tentare di descrivere qui a grandi linee il quadro che ne deriva può servire se non altro a mostrare fino a che punto l'econometria sia oggi integrata nella scienza economica.

Alcuni precursori

Già da tempo alcuni studiosi avevano pensato che si potessero scoprire le leggi del mondo economico mediante l'osservazione, così com'era avvenuto per quelle del mondo fisico; ma fino a qualche decennio fa i risultati erano stati scarsi (v. Pesaran, 1987). In Inghilterra nel XVII secolo la 'legge di King' aveva definito una relazione stabile tra la variazione del raccolto e quella del prezzo del grano; in Germania nel 1857 la 'legge di Engel' aveva specificato come la composizione delle spese delle famiglie variasse in funzione del loro reddito; quasi contemporaneamente in Francia Clément Juglar aveva affermato l'esistenza di un ciclo dell'investimento di durata compresa tra i sette e gli undici anni, e un po' più tardi altri economisti avevano ripreso la stessa idea per studiare le varie periodicità insite nell'evoluzione economica.

Le ricerche induttive si sono moltiplicate all'inizio del nostro secolo, con la pubblicazione dei lavori di Benini (v., 1907) in Italia, di Lenoir (v., 1913) in Francia, di Moore (v., 1914) negli Stati Uniti. Una volta avviato questo movimento, gli emuli furono parecchi, e dopo qualche tempo l'ambizioso tentativo di stimare un modello rappresentante le evoluzioni macroeconomiche di un intero paese si concretò nei lavori pionieristici di J. Tinbergen (v., 1939). Fu questa prima generazione di studi a stimolare la riflessione sul metodo da adottare, permettendo così all'econometria di definire il proprio modo di procedere.

Per dare un giudizio sui risultati, a più di mezzo secolo di distanza dall'impulso iniziale, converrà distinguere almeno due categorie di relazioni. La prima riguarda i 'comportamenti', intendendo questo termine in modo abbastanza ampio da includere ad esempio la dipendenza di una produzione dalle quantità dei fattori impiegati; ciò che distingue questa categoria è il riferimento a un tipo di agente, ai vincoli cui è soggetto e alle decisioni da lui prese. La seconda categoria comprende ciò che caratterizza il funzionamento dei mercati e più in generale tutti i processi socioeconomici di contrattazione. Infine non basta studiare singolarmente ciascuna relazione, e nemmeno un dato gruppo di relazioni simili determinate congiuntamente, ma occorre anche mettersi sul piano dell'economia globale per vedere come progredisce la comprensione del suo evolversi.

Leggi di comportamento

In che modo gli individui determinano le proprie offerte di lavoro, e quali elasticità queste presentano rispetto al livello del salario, al reddito del coniuge, alle altre risorse della famiglia, alle sue caratteristiche demografiche, ecc. (v. Killingsworth, 1983; v. Heckman e McCurdy, 1986)? In che modo i nuclei familiari programmano le proprie spese e la trasmissione del patrimonio ai discendenti (v. Modigliani, 1988; v. Kotlikoff, 1988)? Come modificano i propri consumi in seguito a un cambiamento nelle previsioni di reddito (v. Flavin, 1981)? Come ripartiscono le proprie spese tra i vari beni (v. Deaton, 1986)? A quali vincoli tecnici sono soggette le imprese nella produzione, quali elasticità di sostituzione esistono tra i vari fattori e quali economie di scala sono possibili (v. Jorgenson, 1986)? Come si spiegano le variazioni degli investimenti delle imprese (v. Artus e Muet, 1986)? E quelle della domanda di moneta (v. Poole, 1988)?

Quest'elenco di quesiti non esaurisce tutti gli aspetti dei comportamenti di cui l'econometria tenta di dare una rappresentazione quantitativa; né i riferimenti bibliografici, scelti tra i più recenti, documentano esaurientemente le origini più o meno remote dei problemi e la quantità dei lavori ad essi dedicati, nel passato come nel presente. Si tratta di un'attività troppo vasta per essere qui descritta, ma è possibile darne un'idea con un esempio: lo studio delle fluttuazioni degli investimenti produttivi.

Verso il 1950 l'interpretazione di questo fenomeno faceva capo a tre diverse tesi, ciascuna delle quali metteva in risalto un particolare fattore, considerato implicitamente come predominante o addirittura come esclusivo: la pressione della domanda sulle capacità di produzione, il livello dei profitti realizzati, il livello dei tassi d'interesse. Il lavoro svolto dagli econometristi negli ultimi quarant'anni ha permesso di stabilire il ruolo da assegnare a ciascuna di queste tesi, mettendo in luce altri fattori o proponendo un modo diverso di considerare i fattori in gioco; tuttavia non si è ancora raggiunta la precisione che sarebbe desiderabile per comprendere a fondo il passato e per prevedere gli effetti di certi cambiamenti ipotizzabili, specialmente quando l'interesse non è rivolto solo alle reazioni immediate, ma anche alle conseguenze a medio termine (ad esempio dopo cinque anni).

Oggi si può affermare che il ruolo più evidente spetta alle fluttuazioni della pressione che la domanda di beni rivolta alle imprese esercita sulle loro capacità di produzione: questo fenomeno è detto 'accelerazione', in quanto una domanda in forte crescita stimola gli investimenti e ciò provoca un ulteriore aumento della domanda stessa. Ma oltre a questo fattore ben identificato, la cui influenza è quantificabile con sufficiente precisione, ne intervengono altri, classificati oggi in tre categorie: i costi relativi dei vari fattori di produzione - in particolare il costo del capitale rispetto a quello del lavoro -, la redditività attesa della produzione futura e la facilità di finanziamenti, dovuta specialmente ai profitti realizzati. Vi sono certamente prove a favore della tesi che ciascuna di queste categorie ha la sua importanza, ma la quantificazione rimane carente. Ciò è spiegabile: gli effetti in questione sono per lo più mascherati da quello dell'acceleratore, sono probabilmente molto variabili d'intensità secondo la situazione rispetto alla quale si cerca di valutarli, e infine possono manifestarsi lentamente, il che ne complica alquanto la misurazione. L'econometria dell'investimento ha quindi ancora molto da fare per soddisfare tutte le aspettative degli economisti.

Leggi di mercato e aggiustamenti

Più di trent'anni fa A.W. Phillips (v., 1958) attirò l'attenzione degli studiosi osservando che fra il tasso di variazione annua dei salari nominali e il tasso di disoccupazione, rilevati in Gran Bretagna nell'arco di un secolo, vi era un legame empirico molto semplice. Ebbe così inizio un complesso di ricerche sui fattori che spiegano l'evoluzione dei salari nominali. Fu accertato abbastanza presto che la relazione era meno semplice di quella rappresentata dalla 'curva di Phillips', e che occorreva tener conto soprattutto del ritmo previsto o constatato dell'aumento dei prezzi, ma anche di altri fattori, variabili da un paese all'altro o da un periodo all'altro (v., ad esempio, Grubb, 1986).

Da questi lavori sono emerse comunque delle leggi relativamente stabili. Esse non riflettono direttamente un comportamento ben determinato, ma esprimono piuttosto il risultato di un insieme di fenomeni abbastanza complessi: la concorrenza quasi perfetta esistente in certi mercati del lavoro particolarmente fluidi e atomizzati, la contrattazione a livello di singola impresa o tra le grandi organizzazioni sindacali e padronali, l'intervento governativo, ecc. Alcuni economisti teorici hanno deplorato questa situazione, e talora hanno perfino sostenuto la tesi che non si può dar credito a una relazione empirica di cui non si siano completamente chiariti i fondamenti comportamentali. Questa tesi è evidentemente inammissibile, perché l'osservazione è alla base di ogni conoscenza scientifica e il difetto di comprensione dei motivi dei comportamenti e delle loro interazioni non deve prevalere sull'osservazione delle regolarità che si manifestano direttamente a livello macroeconomico.

La legge che spiega le variazioni del livello medio dei salari può essere chiamata 'legge di mercato', essendo questo termine inteso in un'accezione abbastanza ampia da abbracciare tutti i tipi di contrattazione e da includere eventualmente il potere politico; si potrebbe anche parlare di 'legge di aggiustamento', nella misura in cui la variazione dei salari corrisponde a un aggiustamento parziale degli squilibri delle quantità e dei prezzi che la situazione corrente implica. L'econometria prende anche in considerazione altre leggi di mercato e di aggiustamento, sia per spiegare le variazioni del livello generale dei prezzi, dei tassi d'interesse e dei tassi di cambio, sia per caratterizzare i movimenti più o meno involontari delle scorte, dell'attività e della disoccupazione.

Queste ricerche riguardano questioni disparate. Così da qualche tempo vien fatto spesso di chiedersi se i corsi che si stabiliscono sui mercati finanziari non presentino una volatilità eccessiva rispetto a quanto esigerebbe l'efficienza economica: non saranno oggetto di 'bolle speculative' dovute al fatto che gli operatori sono sensibili soprattutto alle possibilità di guadagno o di perdita a brevissimo termine? Rispondere a questa domanda è difficile, perché non si sa a priori quale sia un'evoluzione dei corsi perfettamente conforme all'efficienza. Spetta comunque proprio all'econometria trarre delle conclusioni al riguardo: nelle diagnosi attuali si tende a riconoscere l'esistenza delle suddette bolle (v. West, 1988), il che implica evidentemente l'opportunità di un controllo dei mercati da parte delle istituzioni centrali.

Costruzione di modelli macroeconometrici

Nello studio dei grandi fenomeni macroeconomici gli econometristi annettono oggi alla ricerca delle periodicità un'importanza molto minore che nella prima metà del secolo. Certamente l'attività economica è soggetta a notevoli fluttuazioni e i ritardi inerenti ad alcuni fenomeni possono favorire la comparsa di componenti con periodicità particolari; ma queste componenti interferiscono tra loro e si combinano con movimenti dovuti a influenze esogene in modo troppo complesso perché la ricerca delle periodicità sia di per sé abbastanza istruttiva. L'obiettivo si è spostato verso la determinazione di leggi e verso la costruzione di modelli econometrici applicabili a un'intera nazione. Tuttavia, come si è visto, l'attuale interesse di alcuni econometristi per le regressioni autovettoriali indica un certo ritorno a intenti più descrittivi (v. Sims, 1980).

La ricerca di una rappresentazione numerica della genesi delle fluttuazioni macroeconomiche, avviata da J. Tinbergen (v., 1939), fu ripresa qualche tempo dopo da L. Klein e applicata a numerosi paesi; il modello di Klein-Goldberger (v. Klein e Goldberger, 1955) servì da esempio a molti altri. Modelli sempre più grandi furono elaborati nelle università, nei centri di ricerca, nelle banche centrali e nelle amministrazioni nazionali e internazionali; questi modelli, affidati a gruppi di specialisti, hanno avuto spesso una parte determinante nella comprensione dei fenomeni macroeconomici (sulla storia e sulla metodologia di queste ricerche v., ad esempio, Artus, Deleau e Malgrange, 1986).

Un modello macroeconometrico può essere considerato come la traduzione operativa e numerica di un modello teorico relativo alle fluttuazioni dell'attività. Per poter analizzare vari aspetti concreti di queste fluttuazioni e di ciò che può influenzarle, si è portati a introdurre parecchie variabili ed equazioni da cui la teoria astrae. La stima delle equazioni sulla base delle serie statistiche fornisce talvolta per i coefficienti valori diversi da quelli immaginati dai teorici; tuttavia il modello conserva la maggior parte delle proprietà dello schema teorico su cui è fondato. Così l'evolversi delle idee sui fattori dominanti della crescita, dell'inflazione e della disoccupazione, insieme all'evolversi delle questioni riguardanti tali fattori, si traduce in qualche modo nella struttura data ai modelli e nella loro utilizzazione.

Con lo stabilire la dipendenza di un insieme di variabili endogene da un insieme di variabili esogene, un modello macroeconomico offre una spiegazione dell'evolversi delle prime in conseguenza dell'evolversi delle seconde; si presta quindi sia alla riflessione sul passato e su ciò che ha determinato la situazione attuale dell'economia, sia a delle previsioni, o proiezioni, sia, infine, allo studio dei prevedibili effetti di differenti scelte di politica economica. L'attendibilità di queste applicazioni dipende evidentemente dal grado di precisione raggiunto dal modello nella rappresentazione delle fluttuazioni dell'attività; questa precisione lascia a desiderare, ma ciò deriva dalla complessità dei fenomeni che gli economisti sono chiamati ad analizzare e dall'incertezza delle conoscenze scientifiche al riguardo. Negli anni settanta sono state espresse riserve apparentemente più gravi a proposito dell'impiego di questi modelli nella definizione delle politiche macroeconomiche; ma l'effettiva importanza di tali riserve è stata esagerata (v. Malinvaud, 1981).Più in generale sono oggetto di recenti indagini econometriche problemi d'ordine molto diverso posti dall'intervento dei poteri pubblici e dalla scelta delle regolamentazioni o delle legislazioni (v. Stone e Peterson, 1978). (V. anche Economia; Metodo e tecniche nelle scienze sociali; Statistica applicata alle scienze sociali).

Bibliografia

Anderson, T. W., The statistical analysis of time series, New York 1971.

"Annales de l'INSEE", n. speciale sull'analisi econometrica dei dati individuali temporali, aprile-settembre 1978.

Artus, P., Deleau, M., Malgrange, P., Modélisation macroéconomique, Paris 1986.

Artus, P., Muet, P.-A., Investissement et emploi, Paris 1986.

Benini, R., Sull'uso delle formule empiriche nell'economia applicata, in "Giornale degli economisti", 1907, XXXV, pp. 1053-1063.

Benzécri, J. P. (a cura di), L'analyse des données, 2 voll., Paris 1973.

Blaug, M., The methodology of economics or how economist explain, Cambridge 1980.

Burns, A. F., Mitchell, W., Measuring business cycles, New York 1946.

Christ, C., The founding of the Econometric Society and Econometrica, in "Econometrica", 1983, LI, 1, pp. 3-6.

Deaton, A., Demand analysis, in Handbook of econometrics (a cura di Z. Griliches e M. Intriligator), vol. III, Amsterdam 1986, pp. 1767-1840.

De Finetti, B., Teoria delle probabilità, 2 voll., Torino 1970.

Flavin, M., The adjustement of consumption to changing expectations about future income, in "Journal of political economy", 1981, LXXXIX, 5, pp. 974-1009.

Gouriéroux, C., Econométrie des variables qualitatives, Paris 1984.

Gouriéroux, C., Monfort, A., Cours de séries temporelles, Paris 1983.

Granger, C., Investigating causal relations by econometric models and cross-spectral methods, in "Econometrica", 1969, XXXVII, pp. 424-438.

Griliches, Z., Intriligator, M., Handbook of econometrics, 3 voll., Amsterdam 1983-1986.

Grubb, D., Topics in the OECD Phillips curve, in "Economic journal", 1986, n. 381, pp. 55-79.

Haavelmo, T., The probability approach in econometrics, in "Econometrica", 1944, XII, suppl.

Heckman, J. J., McCurdy, T. E., Labor econometrics, in Handbook of econometrics (a cura di Z. Griliches e M. Intriligator), vol. III, Amsterdam 1986, pp. 1917-1977.

Hood, W., Koopmans, T. (a cura di), Studies in econometric method, New York 1953.

Jorgenson, D., Econometric methods for modeling producer behavior, in Handbook of econometrics (a cura di Z. Griliches e M. Intriligator), vol. III, Amsterdam 1986, pp. 1841-1915.

Killingsworth, M., Labor supply, Cambridge 1983.

Klein, L. R., Goldberger, A., An econometric model of the United States, 1929-1952, Amsterdam 1955.

Koopmans, T. C., Measurement without theory, in "Review of economic and statistics", 1947, XXIX, pp. 161-172 (tr. it.: Misura senza teoria, in "Rassegna della letteratura sui cicli economici", 1962).

Koopmans, T. C. (a cura di), Statistical inference in dynamic economic model, New York 1950.

Kotlikoff, L. J., Intergenerational transfers and savings, in "Journal of economic perspectives", 1988, II, 2, pp. 41-58.

Leamer, E., Specification searches. Ad hoc inference with nonexperimental data, New York 1978.

Lenoir, M., Études sur la formation et le mouvement des prix, Paris 1913.

Leontief, W., Econometrics, in A survey of contemporary economics (a cura di H. S. Ellis), Philadelphia 1948, pp. 388-411.

Malinvaud, E., Méthodes statistiques de l'économétrie, Paris 1964 (tr. it.: Metodi statistici dell'econometria, Torino 1971).

Malinvaud, E., Econometrics faced with the needs of macroeconomic policy, in "Econometrica", 1981, IL, 6, pp. 1363-1375.

Malinvaud, E., Econometric methodology at the Cowles commission: rise and maturity, in "Econometric theory", 1988, IV, pp. 187-209.

Modigliani, F., The role of intergenerational transfers and life cycle saving in the accumulation of wealth, in "Journal of economic perspectives", 1988, II, 2, pp. 15-40.

Moore, H., Economic cycles: their law and cause, New York 1914.

Pesaran, M. H., Econometrics, in The new Palgrave. A dictionary of economics (a cura di J. Eatwell, M. Milgate, P. Newman), vol. I, London 1987, pp. 8-22.

Phillips, A. W., The relation between unemployment and the rate of change of money wage rates in the United Kingdom (1861-1957), in "Economica", 1958, XXV, pp. 283-299.

Pierce, D., Haugh, L., Causality in temporal systems, in "Journal of econometrics", 1977, V, pp. 265-294.

Poole, W., Monetary policy lessons of recent inflation and disinflation, in "Journal of economic perspectives", 1988, II, 3, pp. 73-100.

Robbins, L. S., An essay on the nature and significance of economic sciences, London 1932 (2 ed. ampliata 1935) (tr. it.: Saggio sulla natura e importanza della scienza economica, Torino 1953).

Savage, L., The foundations of statistics, New York 1954.

Sims, C., Macroeconomics and reality, in "Econometrica", 1980, XLVIII, pp. 1-48.

Stone, R., Peterson, W. (a cura di), Econometric contribution to public policy, London 1978.

Theil, H., Principles of econometrics, New York 1971.

Tinbergen, J., Statistical testing of business cycles theories, Genève 1939.

Tukey, J., Exploratory data analysis, Reading, Mass., 1977.

West, K., Dividend innovation and stock price volatility, in "Econometrica", 1988, I, pp. 37-61.

Zellner, A., An introduction to Bayesian inference in econometrics, New York 1971.