Elaborazione neuromorfa dei segnali sensoriali con circuiti VLSI analogici
Elaborazione neuromorfa dei segnali sensoriali con circuiti VLSI analogici
I circuiti neuromorfi sono circuiti analogici che implementano modelli di sistemi biologici per l'elaborazione dei segnali sensoriali. Poiché sono soggetti agli stessi vincoli fisici delle loro controparti biologiche, essi possiedono strutture organizzative simili e adottano strategie analoghe per ottimizzare i consumi ed essere meno disturbati dal rumore. Le retine di silicio e altri chip per la visione neuromorfa, costruiti come modelli dei sistemi visivi biologici, possiedono efficienti algoritmi per l'elaborazione preliminare dei segnali sensoriali. La ricerca si sta interessando anche allo studio di reti per l'elaborazione generale che usano modelli dettagliati dei neuroni. Sono stati costruiti semplici sistemi neuromorfi usando reti di neuroni di silicio e chip neuromorfi come dispositivi per l'elaborazione di segnali sensoriali.
Introduzione
L'ingegneria neuromorfa applica i principi computazionali scoperti negli organismi biologici a quei compiti che i sistemi biologici svolgono con facilità, ma che si sono dimostrati difficili da realizzare con le tecniche ingegneristiche tradizionali (Mead, 1990). Questi principi computazionali riguardano compiti specifici quali il movimento guidato dalla visione, la localizzazione uditiva, l'olfatto, il riconoscimento di oggetti, il controllo cosciente degli arti e la locomozione.
Finora i più grandi successi dei circuiti analogici integrati su grandissima scala (aVLSl, analog Very Large Scale Integration) neuromorfi sono stati ottenuti nell'emulazione della trasduzione ed elaborazione del segnale che avviene in sistemi sensoriali periferici quali la retina e la coclea. Gli organi sensoriali periferici sono il naturale punto di inizio per lo sviluppo di un sistema neuromorfo analogico, dato che la luce che cade sulla retina o le onde sonore che entrano nella coclea sono segnali analogici continui. Inoltre, queste strutture sono facilmente accessibili ai neurobiologi e il loro ruolo funzionale è noto, almeno a grandi linee, per cui molto si conosce della loro biologia. Queste strutture hanno anche un'organizzazione relativamente semplice, essendo costituite da griglie di elementi di elaborazione simili, che interagiscono solo con i primi vicini. Questi circuiti hanno una struttura bidimensionale ripetitiva, 'cristallina', che può essere riprodotta sulla superficie di un singolo chip, e l'output dell'elaborazione può essere letto da un campionamento a scansione.
Le retine di silicio
Lo strato plessiforme esterno (OPL, Outer Plexiform Layer) della retina dei vertebrati ha suscitato l'interesse degli ingegneri neuromorfi perché è in grado di svolgere operazioni di analisi d'immagine altamente ottimizzate usando solamente tre strati di neuroni: i fotorecettori, le cellule orizzontali e le cellule bipolari. In ambienti naturali, il profilo di luminanza che viene impresso sulla griglia di fotorecettori è il risultato della diversa riflessione della luce da parte delle superfici degli oggetti presenti nell'ambiente. Tipicamente, la riflettanza degli oggetti in una data scena varia in un intervallo che copre un ordine di grandezza. Per avere la situazione ottimale, l'intervallo operativo dei fotorecettori dovrebbe essere regolato per coprire solo questo spettro di livelli di illuminazione. Se l'intervallo su cui operano i fotorecettori risulta più ristretto di quello della scena, l'informazione sulla luminanza verrà persa a causa della saturazione o dell'alto livello di soglia. Se invece l'intervallo dei fotorecettori risulta più ampio di quello della scena, i fotorecettori codificheranno la luminosità con una risoluzione inferiore a quella ottimale. D'altra parte, scene, diverse sono caratterizzate da livelli di illuminazione estremamente variabili. L'illuminazione varia di oltre 6 ordini di grandezza quando si passa dalla luce del giorno a quella delle stelle. Di conseguenza, mentre l'intervallo operativo della retina deve essere ottimizzato per ogni singola scena, allo stesso tempo deve adattarsi a variazioni su 5-6 ordini di grandezza, in modo da garantire che la risposta della retina sia conforme al livello di illuminazione prevalente.
Sarebbe utile se la retina fosse in grado di rispondere a qualche caratteristica invariante del profilo di luminanza, in modo che la relazione di intensità luminosa tra oggetti diversi risulti invariante rispetto all'illuminazione. l fotorecettori biologici sono in grado di fado rilevando il contrasto dell'immagine (ΔL/L) piuttosto che la sua luminosità assoluta (L). A questo scopo essi riportano il logaritmo della luminosità, in modo che il contrasto ΔL/L sia invariante rispetto all'illuminazione.
Il pixel di base
A partire dalla fine degli anni Ottanta sono state sviluppate numerose retine di silicio su singoli chip a VLSI (Mahowald e Mead, 1989; Boahen e Andreou, 1992) che possiedono le importanti proprietà dell'OPL più sopra accennate. Questi circuiti consistono di solito in una griglia di pixel (il più piccolo elemento in cui è scomposta l'immagine originale), che realizzano una codifica del contrasto dell'immagine con adattamento. I pixel controllano i nodi di una griglia resistiva esagonale, la quale fornisce un filtraggio spaziotemporale.
Vi sono due famiglie di circuiti retinici: quella dei circuiti che lavorano in tensione (Mahowald e Mead, 1989; Delbriick, 1994) e quella dei circuiti che lavorano in corrente (Bohaen e Andreou, 1992).
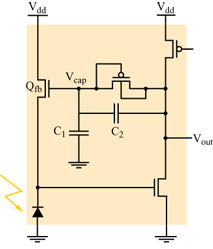
La modalità di funzionamento in tensione. - Il fotorecettore della retina di silicio originale, sviluppato da C. Mead e M. Mahowald, era un circuito che lavorava in tensione, e integrava un fotodiodo logaritmico in un amplificatore ad alto guadagno. Il progetto originale è stato molto migliorato da T. Delbriick e Mead (Delbriick, 1994). Il loro recettore a 5 transistor (fig. 1) presenta una risposta logaritmica su un intervallo dinamico di l÷2 ordini di grandezza a un fissato livello di adattamento, e opera su un intervallo dinamico totale (che include l'adattamento) di più di 6 ordini di grandezza.
Come nel circuito originale del fotorecettore, il recettore di Delbriick integra un fotodiodo in un amplificatore invertente ad alto guadagno. La risposta di questo amplificatore provoca una retro azione negativa su un transistor N-FET, in serie con il fotodiodo. L'effetto della retroazione è quello di fissare l'output del fotodiodo, il che è equivalente a fissare l'input dell'amplificatore ad alto guadagno, e in questo modo accelerare la risposta del circuito del recettore. Il guadagno del circuito per piccoli segnali dipende dal rapporto tra capacità (C 1+C₂)/C 1, e il punto di lavoro del circuito dipende dalla tensione Vcap, che è proporzionale alla carica sul gate di β (v. figura 1). La carica può accumularsi o diminuire passando sul gate, attraverso l'elemento di adattamento posto tra il gate e l'output del recettore. Per esempio, se la tensione di uscita Vcap del circuito rimane alta rispetto alla tensione Vcap, allora la corrente scorrerà attraverso l'elemento di adattamento, gradualmente caricherà il gate e quindi ripristinerà la tensione di output dell' amplificatore del fotorecettore.
Questo fotorecettore ad alto guadagno può essere usato in connessione con altri circuiti per fornire un'elaborazione preliminare del segnale visivo. Le applicazioni più comuni comportano l'uso di grandi griglie di fotorecettori, spesso disposti su celle esagonali e con accoppiamento ai primi vicini. I fotorecettori determinano il potenziale dei nodi di una rete resistiva e capacitiva esagonale, che a sua volta fornisce una media locale spaziotemporale degli output dei fotorecettori. In questo caso la risposta di ogni pixel della retina è proporzionale alla differenza tra il segnale del fotorecettore e la media pesata spaziotemporale dei segnali dei fotorecettori vicini.
A causa delle difficoltà tecniche della comunicazione tra chip (v. il saggio di R. Douglas, M.A. Mahowald e A. Whatley, in questo volume), le retine di silicio attuali contengono in un unico chip i fotorecettori e i circuiti di elaborazione. Le risposte campionate di ogni elemento sono campionate da un meccanismo a scansione e, dopo un'opportuna conversione, sono mostrati sullo schermo di un monitor. Recentemente sono state sviluppate alcune varianti del circuito di scansione che permettono di interfacciare la retina di silicio a un comune personal computer, in modo che le retine neuromorfe possano essere usate per acquisizioni video da computer al posto delle telecamere digitali commerciali (CCD, Charge Coupled Device, dispositivo ad accoppiamento di carica). Vi sono anche varianti della retina di silicio che producono output adatti a un sistema neuromorfo a più chip, che usa un protocollo di comunicazione tra i singoli chip basato sulla rappresentazione indirizzo-evento (AER, Address Event Representation; Mahowald, 1992; Douglas et al., 1995). A questo proposito si veda sempre il saggio di R. Douglas, M.A. Mahowald e A. Whatley in questo volume.
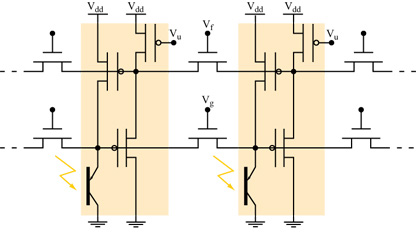
La modalità di funzionamento in corrente. - K. Boahen e A. Andreou hanno proposto un progetto di retina alternativo al precedente. La loro retina è basata su circuiti translineari, e l'elemento foto sensibile è un transistor bipolare verticale, la cui corrente all'emettitore è proporzionale all'intensità della luce incidente. Il circuito permette alla corrente indotta dalla luce di diffondersi nel tempo e nello spazio. La diffusione avviene tramite due reti di elementi diffusori orizzontali (fig. 2) che sono realizzati con transistor N-FET. Il primo strato di diffusione emula gli accoppiamenti eccitatori laterali tra i coni fotorecettori della retina biologica. L'output di questo strato eccita il secondo strato di diffusori, che emula gli accoppiamenti laterali eccitatori tra le cellule orizzontali dell'OPL. Il secondo strato produce poi una retroazione per inibire il primo strato, dove questo segnale viene usato per controllare la sensibilità alla luce. Il risultato finale è un controllo automatico e locale del guadagno.
La retina di silicio di Boahen-Andreou è un notevole esempio di ingegneria neuromorfa. Ogni pixel è costituito solo da 4 transistor (v. figura 2). Andreou ha calcolato che una versione della loro retina con 210 x 230 pixel è in grado di effettuare in un secondo 10¹² calcoli a bassa precisione. In queste condizioni la potenza consumata dal chip è di soli 50 mW, il che significa che l'energia dissipata per operazione è di 0,05 pl Questa piccola dissipazione deve essere confrontata con quella, di gran lunga maggiore (10⁵ pJ per operazione) di un calcolatore digitale dell'ultima generazione, che deve commutare lo stato di molti transistor per effettuare ogni singola operazione.
Chip specifici per l'elaborazione dei segnali sensoriali
Pixel per la rivelazione del movimento
Lo strato plessiforme interno della retina è meno conosciuto di quello esterno e si pensa che debba svolgere un qualche ruolo nell'elaborazione del movimento. Nei vertebrati inferiori, come la rana, lo strato plessiforme interno ha complesse interazioni sinaptiche che danno origine a rivelatori di caratteristiche invarianti. La complessità dell' elaborazione del segnale visivo è una caratteristica desiderabile quando l' output della retina viene usato direttamente per produrre comportamenti specializzati (Horiuchi et al., 1991; 1992). Il prezzo da pagare per integrare un'elaborazione più complessa nella matrice retinica è che i fotorecettori devono essere sparsi in zone distanti del chip per fare posto ai circuiti aggiuntivi. Uno dei primi esempi di retina di silicio complessa è la retina sensibile alla velocità costruita da Delbriick (Delbriick, 1993). Questo chip contiene dei circuiti analogici addizionali per individuare oggetti in movimento. In corrispondenza di ogni pixel, la retina genera tre output indipendenti, che sono sensibili solo a una particolare velocità e a una particolare direzione di movimento, indipendentemente dal contrasto dello stimolo.
Rilevatori di velocità
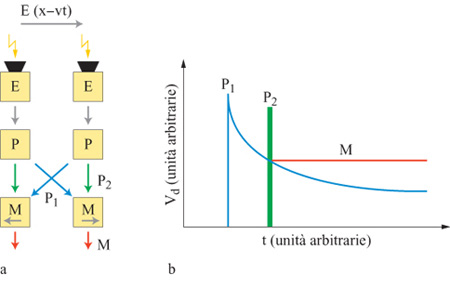
Più di recente, J. Kramer e collaboratori (1996a) hanno sviluppato un sensore di velocità elementare che è sensibile agli stimoli a basso contrasto, indipendentemente dall'ampiezza del contrasto dello stimolo, e selettivo per velocità su 3 ordini di grandezza. La velocità dell'immagine viene calcolata come rapporto tra la separazione spaziale tra due fotorecettori (che è ovviamente nota) e il tempo, misurato, che impiega il bordo di una figura a passare da un fotorecettore all'altro. Il sensore (fig. 3) è estremamente compatto, e quindi può essere facilmente integrato in chip che devono computare il flusso ottico di un' intera immagine (cioè la proiezione bidimensionale di un campo di velocità tridimensionale sul piano dove si forma l'immagine retinica). Esso utilizza un algoritmo che misura il tempo di traslazione necessario alle linee ad alto contrasto dell'immagine (v. figura 3) per passare tra due fotorecettori. Quando un fotorecettore individua una variazione di contrasto, vengono generati due segnali: un impulso rapido, P₂, e un segnale a decadimento lento, P₁ (con profilo logaritmico). L'impulso viene trasmesso al circuito di rivelazione di movimento, M, che fa parte dello stesso elemento cui appartiene il fotorecettore, mentre il segnale logaritmico viene trasmesso all'elemento di rivelazione del movimento vicino.
Per esempio, per un moto verso destra, la linea ad alto contrasto verrà prima rivelata dal fotorecettore di sinistra, e poi da quello di destra. Di conseguenza, il rivelatore di movimento M di destra vede prima l'inizio del segnale P₁, che decade, e poi l'impulso P2. Questo impulso viene usato per leggere la tensione di P1 e memorizzarla in M. La tensione analogica indicata con M nella figura 3b è proporzionale al ritardo tra la comparsa del bordo sul primo pixel e la comparsa dello stesso bordo sul secondo, e codifica la velocità del moto verso destra.
Rivelatori del punto focale di espansione
Quando un osservatore si sposta all'interno del suo ambiente, i bordi ad alto contrasto delle figure sembrano muoversi. l vettori velocità che essi generano sono radiali, ed escono tutti da un punto chiamato punto locale di espansione. In uno spostamento puramente traslatorio, questo punto corrisponde alla direzione del movimento. Un veicolo che si sposta in un ambiente in cui gli oggetti sono fermi può calcolare la direzione del proprio movimento semplicemente misurando i vettori velocità della scena (che generano un campo di flusso ottico) e individuando la posizione del punto focale di espansione.
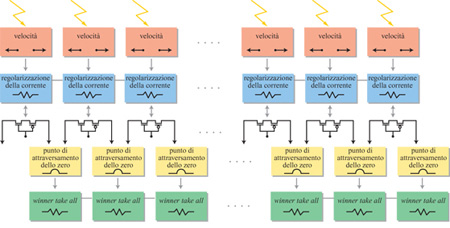
G. lndiveri e collaboratori (1996) hanno progettato un'architettura parallela in a VLSI che, integrando i dati sul flusso ottico, ottenuti da griglie di sensori di velocità elementari come quelli sopra descritti, può valutare la direzione del movimento. Avendo scelto un campo specifico di applicazione (il moto di veicoli su ruota), gli autori hanno potuto fare delle ipotesi a priori e semplificare il progetto del dispositivo a VLSI (decidendo, per esempio, di rivelare i cambiamenti di direzione solo lungo l'asse orizzontale). In figura (fig. 4) viene mostrato un diagramma a blocchi dell'architettura del dispositivo. Lo stadio di input dell'architettura è una sequenza unidimensionale di sensori elementari di velocità, che misurano la rapidità e la direzione del moto dei bordi delle figure usando dei fotorecettori presenti sul chip. Ogni sensore di velocità ha un'uscita differenziale, con un terminale per una direzione del moto, e l'altro terminale per l'altra direzione. Il segnale differenziale in tensione di ogni sensore di velocità viene quindi convertito in corrente. A seconda della direzione del moto dello stimolo, ogni pixel fornisce in output una corrente costante positiva o negativa. In particolare, i vettori velocità che puntano verso sinistra sono codificati con correnti positive, mentre quelli che puntano verso destra sono codificati con correnti negative. Il punto focale di espansione, che corrisponde alla posizione spaziale in cui i vettori velocità cambiano direzione, sarà rappresentato dal punto in cui le correnti cambiano segno. Se le correnti di pixel vicini cambiano segno, diremo che in quel punto c'è un attraversamento dello zero. Questi attraversamenti sono rivelati da un circuito ad hoc, che calcola la correlazione tra la corrente negativa di un pixel e la corrente positiva di quello adiacente. Questo circuito determina anche la pendenza della curva che attraversa lo zero. La selezione dell'attraversamento con la massima pendenza (che corrisponde alla posizione più probabile per il punto focale di espansione) viene effettuata usando un circuito con eccitazione distribuita e isteresi locale (lndiveri, 1997) detto winner take all (il vincitore prende tutto, ovvero l'unità con la massima pendenza sopprime le altre e rimane l'unica attiva).
Tempo di contatto
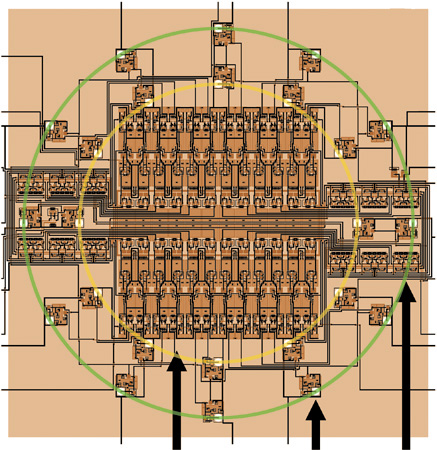
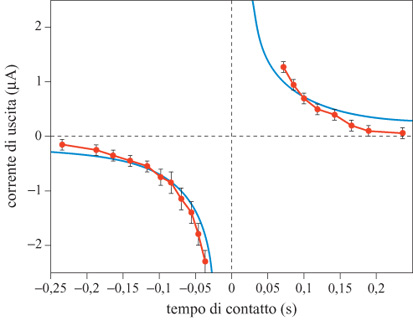
Un'altra utile quantità che può essere estratta da un campo di flusso ottico ottenuto con sensori di velocità in a VLSI è il tempo che manca al contatto con un oggetto che copre, parzialmente o completamente, il campo visivo. Il tempo di contatto è definito come il tempo che impiegherebbe l'osservatore a venire in contatto con l'oggetto, assumendo che la velocità relativa tra osservatore e oggetto rimanga costante. Per calcolare il tempo di contatto con un oggetto che si avvicina è necessario misurare la velocità di espansione della proiezione dell'oggetto sulla retina. G.T. Poggio e collaboratori (1991) hanno proposto un semplice algoritmo per estrarre dalle misure locali della velocità alcune proprietà globali del campo di flusso ottico, come la rotazione o l'espansione. L'algoritmo proposto, ispirato ai modelli biologici e quindi adatto per la realizzazione in a VLSI neuromorfo, si basa sulla versione bidimensionale del teorema della divergenza di Gauss: si tratta di calcolare la somma su un cammino chiuso della componente normale del flusso ottico, misurata lungo il cammino stesso. Kramer e collaboratori (1996b) hanno progettato un chip aVLSl che realizza questo algoritmo. Tale dispositivo usa 12 sensori elementari di velocità disposti lungo un cerchio. Ogni sensore misura la componente radiale della velocità dello stimolo, e somma la sua corrente di output a quelle provenienti dagli altri sensori in un nodo comune globale (fig. 5). Il circuito produce delle stime ragionevolmente accurate del tempo di contatto per una figura in avvicinamento o in allontanamento costituita di anelli concentrici centrati sul punto focale di espansione, o per uno stimolo a spirale posto su un disco rotante che simula il moto di avvicinamento o allontanamento. In figura (fig. 6) è riportato il grafico della corrente media di output, in risposta allo stimolo a spirale, in funzione del tempo simulato di contatto. La relazione che ci si aspetta prevede che la corrente di output sia inversamente proporzionale al tempo di contatto. Questa relazione corrisponde qualitativamente all'andamento osservato, e il segno, che indica espansione o contrazione, viene codificato in maniera affidabile.
Emulazione dell'elaborazione dell'immagine nella mosca
Le mosche fanno affidamento per sopravvivere sull'informazione riguardante il moto che viene loro fornita dalla vista. Si sa che l'informazione sul moto è alla base di molti comportamenti importanti, tra cui la stabilizzazione del volo, la discriminazione di piccoli oggetti dallo sfondo mediante la parallasse del moto e la stima del tempo di contatto per posarsi con sicurezza sugli oggetti. I circuiti neuronali che sono alla base di queste capacità sono ben conosciuti.
Ovviamente l'elaborazione del moto nella mosca può insegnarci molte cose, dal momento che questo sistema biologico può orientarsi nel moto con un piccolo numero di recettori (Musca domestica ha solo 24.000 recettori) e usando solo pochi milliwatt di potenza. La disposizione retinotopica delle sottounità del sistema visivo rende questo sistema riproducibile su silicio.
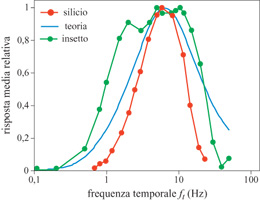
R. Harrison e C. Koch (1998) hanno progettato un rivelatore elementare di movimento basato sulle correlazioni. Il dispositivo, realizzato in a VLSI, è a basso consumo, asincrono, e i fotorecettori integrati rispondono al movimento in tempo reale. I segnali dei fotorecettori sono divisi in due canali: uno per le risposte all'attivazione e l'altro per le risposte alla disattivazione. Tutti i segnali, rappresentati da correnti, sono elaborati da circuiti translineari, i quali sfruttano il comportamento esponenziale che hanno i transistor MOS quando lavorano nella regione sotto so glia. Di recente è stata scoperta un'altra proprietà di adattamento del sistema visivo della mosca: la costante di tempo del sistema di rivelazione del movimento, che determina la posizione del picco nelle curve di adattamento (fig. 7), si adatta alla velocità delle caratteristiche presenti nella scena visiva.
S. Liu (1996) ha sviluppato un circuito che simula alcune caratteristiche del sistema visivo della mosca: l'adattamento della costante di tempo nel sistema di rivelazione del movimento e le risposte selettive alla direzione delle cellule nel disco lobulare. I filtri dei circuiti adattivi regolano le proprie costanti di tempo sulla frequenza temporale dell'input. Questo processo di adattamento permette al sistema di rivelazione del movimento di rispondere in modo affidabile in un intervallo di quattro ordini di grandezza delle frequenze. Grazie al processo di adattamento, il sistema di rivelazione del movimento è altamente sensibile alle deviazioni del moto da un livello medio. I risultati del chip confermano la validità del modello: la costante di tempo dei circuiti si adatta alle frequenze dello stimolo visivo.
Reti per l'elaborazione generale
I sistemi sensoriali a VLSI descritti in precedenza possiedono elementi di elaborazione piuttosto astratti, che sono specializzati a svolgere il loro compito invece di essere composti da elementi di impiego generale, quali i neuroni. Le connessioni tra gli elementi di elaborazione sono cabIate, non riconfigurabili. Fortunatamente i sotto sistemi sensoriali hanno una struttura molto regolare, che è dominata da connessioni di tipo locale. In questi casi è possibile connettere tra loro su un singolo chip alcune migliaia di nodi neurali. Tuttavia, andando oltre lo stadio sensoriale di elaborazione, le connessioni diventano più complesse, e di pari passo si complicano le caratteristiche degli elementi di elaborazione, che devono ricevere e stabilire connessioni con molti dei nodi con cui devono interagire (spesso migliaia).
Una rete altamente connessa può essere costruita solo se viene distribuita su diversi chip. Vi sono molte strategie per dividere la rete tra chip. Di solito, queste strategie prevedono la valutazione di tre elementi diversi: le connessioni (sinapsi) ai nodi di elaborazione (neuroni), le relazioni input-output del nodo di elaborazione e le vie di comunicazione (assoni) che regolano l'instradamento (routing) dei segnali.
Qualunque sia la strategia impiegata, si cerca generalmente di riutilizzare lo stesso hardware per provare diverse architetture neuronali. Questo obiettivo richiede lo sviluppo di neuroni di silicio generali, tali cioè che le loro proprietà bio fisiche e le loro connessioni possano essere riconfigurate per adattarsi a diverse tipologie di neuroni. Inoltre, è necessario adottare una strategia di comunicazione che possa gestire l'enorme convergenza e divergenza di sistemi neuronali generali.
Il neurone di silicio
l neuroni di silicio neuromorfi imitano il comportamento elettro fisiologico dei neuroni biologici. L'imitazione del comportamento viene realizzata usando le stesse tecniche organizzative delle tradizionali simulazioni numeriche di neuroni biologici. La membrana neuronale continua che ricopre il dendrite e il soma viene divisa in una serie di compartimenti omogenei e isopotenziali (Koch e Segev, 1989; Traub e Miles, 1991). La connessione tra i compartimenti riproduce la morfologia spaziale della cellula scelta come modello. In generale, un maggior numero di compartimenti porta a una simulazione più accurata. La risoluzione della segmentazione è il risultato di un compromesso: i compiti cui deve adempiere il modello, le risorse impiegate per ogni compartimento e il livello di tolleranza degli errori. Per esempio, neuroni con un numero di compartimenti compreso tra 5 e 30 sono un buon compromesso, comunemente accettato, per simulazioni digitali di circuiti corticali o dell'ippocampo.
J.G. Elias (Elias, 1993; Northmore e Elias, 1999) ha costruito dei neuroni neuromorfi in VLSI con 112 compartimenti passivi, che costituiscono un modello per le perdite della membrana cellulare e per la resistenza assiale del liquido intracellulare. Negli anni Novanta è diventato chiaro che i dendriti neuronali non sono semplicemente cavi passivi, ma che la tensione e le conduttanze, sensibili alle concentrazioni di ioni, giocano un ruolo importante nel filtraggio spaziotemporale dei segnali trasmessi attraverso i dendriti (Johnston e Wu, 1995; Koch, 1998). Ciò significa che anche i dispositivi neuromorfi dovrebbero essere capaci di elaborazione dendritica attiva.
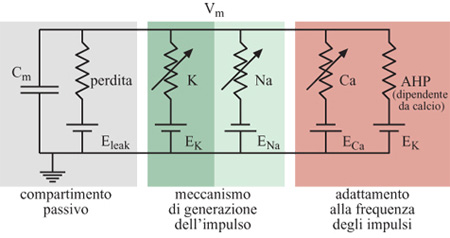
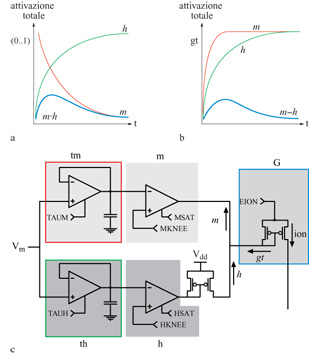
Le conduttanze attive delle membrane neuronali biologiche controllano il flusso della corrente ionica tra i vari potenziali ionici di inversione e la tensione di membrana sulla capacità di membrana. Queste conduttanze attive sono in genere sensibili sia al potenziale di membrana, sia alla concentrazione di uno specifico ione. La figura (fig. 8) mostra un modello elettrico semplificato per un compartimento del soma di una cellula piramidale. Nei neuroni di silicio proposti da Mahowald e Douglas (1991), i compartimenti dendritici e somatici che costituiscono il neurone che si vuole riprodurre sono ricchi di sottocircuiti modulari a VLSl, ognuno dei quali emula una particolare conduttanza ionica (fig. 9). Ognuno dei moduli è una variante di un circuito prototipo per la conduttanza ionica che obbedisce ai principi di Hodgkin e Huxley (Mahowald e Douglas, 1991; Rasche et al., 1998).
Gli amplificatori a transconduttanza sono gli elementi alla base dei circuiti usati per emulare le conduttanze dipendenti dalla tensione. Questi dispositivi hanno una relazione corrente-tensione di tipo sigmoidale, simile a quella osservata in condizioni stazionarie per le conduttanze biologiche dei canali di membrana attivi. Filtri temporali passa-basso forniscono le necessarie costanti di tempo. L'interazione di circuiti separati per l'attivazione e la disattivazione produce i profili temporali, di forma approssimativamente a campana, osservati, per esempio, nel caso della conduttanza del sodio. Questa interazione è moltiplicativa nelle simulazioni convenzionali per la conduttanza (v. figura 9a), mentre nei neuroni di silicio viene riprodotta con un meccanismo di sottrazione (v. figura 9b).
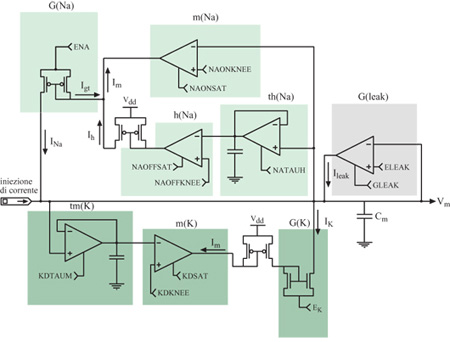
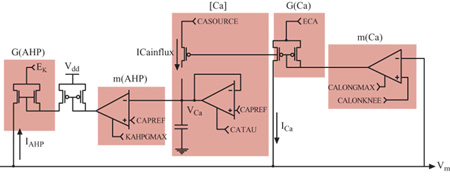
Quando viene opportunamente configurato, il neurone di silicio mostra un comportamento elettro fisiologico simile a quello delle cellule piramidali reali. l cambiamenti di conduttanza e la cinetica delle conduttanze di alcuni canali rendono talune caratteristiche della generazione del potenziale d'azione, come l'adattamento alle frequenze degli impulsi, simili a quelle osservate nella controparte biologica. Anche la distribuzione degli intervalli tra impulsi successivi è simile a quella misurata in vitro da neuroni piramidali. Il neurone di silicio attualmente usato per riprodurre l' elettrofisiologia del soma consiste in un compartimento somatico e in un semplice carico dendritico. Il soma comprende quattro conduttanze attive e una passiva, corrispondenti alle conduttanze semplificate illustrate nella figura 8. In figura (fig. 10) è mostrato il circuito analogico per il meccanismo di generazione del potenziale d'azione che include le conduttanze del sodio, del potassio e di perdita passiva (leak). Nella figura successiva (fig. 11) sono rappresentati i circuiti che emulano la conduttanza del calcio, l'elemento che regola la concentrazione del calcio [Ca], e quello per la conduttanza del potassio, che dipende dal calcio (AHP, Afier Hyperpolarizing Potassium, potassio dopo iperpolarizzazione). Si assume che gli ioni calcio entrino nel soma attraverso una conduttanza del calcio a soglia elevata, dunque solo durante l'emissione di un impulso, e non semplicemente quando la depolarizzazione della membrana è sotto soglia. L'elemento di concentrazione, [Ca], tiene conto della concentrazione del calcio intracellulare. La conduttanza AHP viene attivata aumentando la concentrazione del calcio e allungando l'intervallo tra un impulso e l'altro, il che porta all'adattamento della frequenza di emissione (Rasche et al., 1998).
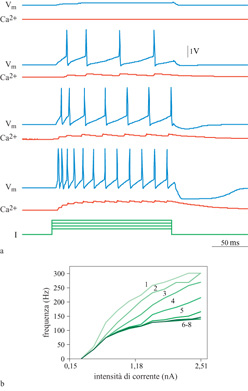
In figura (fig. 12) sono mostrati degli esempi di potenziale d'azione prodotti dall'iniezione intrasomatica di una corrente costante. Si può vedere l'adattamento della frequenza di emissione: gli intervalli tra impulsi sono brevi all'inizio, poi aumentano in durata fino a quando non si giunge a uno stato stazionario. Nella figura 12b è riprodotta una famiglia di funzioni di attivazione di output (cioè di curve correntefrequenza) per questo neurone. La curva più a sinistra rappresenta la risposta per il primo intervallo tra due impulsi successivi. Le altre curve mostrano le risposte per gli intervalli successivi, durante i quali il neurone si adatta progressivamente. Per il primo intervallo la relazione corrente-frequenza ha una grossa pendenza iniziale che va in saturazione per correnti più forti. La saturazione è dovuta all'effetto ritardante sull'inizio dell'impulso successivo dovuto al cambiamento iperpolarizzante nella conduttanza (causato da K) che segue l'impulso. La pendenza delle curve successive diminuisce all'aumentare della conduttanza che si adatta (AHP).
L'aspetto più interessante dei neuroni di silicio risiede nella possibilità di integrarli in reti neurali artificiali di grandi dimensioni. I neuroni semplificati (per esempio quelli basati su un meccanismo di integrazione ed emissione, integrate-and-fire), che vengono usati nella maggior parte delle reti artificiali, hanno una funzione di attivazione ben precisa. Nei neuroni reali la funzione di attivazione non è così semplice, ma dipende dallo stato delle varie conduttanze del soma e dei dendriti. Siccome i neuroni di silicio imitano il comportamento elettrofisiologico dei neuroni reali, essi dovrebbero avere una funzione di attivazione che non deve necessariamente essere specificata in modo esplicito. Questa proprietà è utile per realizzare sistemi nervosi artificiali che usino principi di elaborazione neurale più realistici di quelli adottati finora dalle reti neurali. Inoltre, l'uso di neuroni biologicamente più realistici rende più stretto il legame tra le applicazioni ingegneristiche delle reti neurali e gli esperimenti biologici, che forniscono utili elementi per la comprensione di queste reti.
La corteccia di silicio
L'elaborazione che può essere effettuata da un singolo chip è limitata dall'area di silicio, e la sua utilità è limitata dall'accesso ai canali di input e output. Per esempio, le retine di silicio possono avere alcune migliaia di pixel, ma si possono stabilire solo un centinaio di contatti tra il circuito e i fili macroscopici esterni alla superficie del chip. L'obiettivo degli ingegneri neuromorfi è quello di incorporare molti di questi chip, in grado di svolgere diversi tipi di elaborazione, in un sistema capace di avere un comportamento. A tale scopo sono stati sviluppati numerosi metodi per permettere la comunicazione tra chip analogici (Lazzaro et al., 1993; Mahowald, 1994; Boahen, 1996; Murray, 1999) e superare le limitazioni sui canali di input e output, fino ad arrivare alla costruzione dei primi semplici sistemi neuromorfi a più chip.
Noi abbiamo sviluppato un protocollo di comunicazione tra chip basato su una tecnica di multiplex digitale asincrono, che utilizza un protocollo AER (v. il saggio di R. Douglas, M.A. Mahowald e A. Whatley, in questo volume). Questa tecnica ha le caratteristiche di una modulazione di frequenza degli impulsi in multiplex, controllata dagli eventi. L'indirizzo del nodo sorgente dell'evento viene trasmesso, durante l'impulso, a tutti i nodi di elaborazione che si trovano in una regione definita, i quali decodificano gli indirizzi neurali trasmessi.
Analogamente ai potenziali d'azione neuronali, gli eventi di questo sistema sono eventi digitali stereotipati, e gli intervalli tra gli eventi sono variabili analogiche. Ogni evento è una parola digitale, che rappresenta l'identità del neurone che ha generato il potenziale d'azione. Questo evento digitale, nel momento in cui viene generato il potenziale d'azione, viene messo su un bus di comunicazione comune, che di fatto si comporta, grazie al multiplex, come un assone universale. In questo modo l'informazione viene codificata nella sequenza temporale degli eventi.
Sistemi neuromorfi
Corrispondenza stereoscopica
Il primo sistema neuromorfo a più chip funzionante è stato descritto da Mahowald (1992). Si tratta di un sistema stereoscopico che consiste in due retine di silicio, le quali trasmettono, tramite il protocollo AER, i dati relativi alle immagini da loro rilevate a un terzo chip per la corrispondenza stereoscopica. Questo sistema calcola la profondità stereoscopica degli oggetti a mano a mano che essi si muovono nel campo visivo delle retine.
Nei sistemi biologici, l'informazione sulla profondità stereoscopica non è subito disponibile nelle immagini bidimensionali delle retine. Essa emerge piuttosto nelle prime fasi dell' elaborazione visiva corticale, grazie alla fusione dei dati retinici nel contesto dei vincoli fisici che regolano l'esistenza di oggetti estesi nel mondo reale. Questi vincoli devono essere primitivi, perché il sistema visivo può facilmente risolvere problemi di discriminazione tra stereo grammi di punti casuali (Julesz, 1971), che non contengono indizi cognitivi per la soluzione del problema. Gli esperimenti di psicofisica e di elaborazione del segnale indicano che la fusione stereoscopica di una figura costituita da una distribuzione casuale di punti è un'operazione intrinsecamente non locale e non lineare, che probabilmente richiede una retro azione positiva (Julesz, 1971; Marr, 1982). Per queste ragioni i modelli basati sulla visione stereoscopica sono interessanti sia per capire le funzioni corti cali, sia per sviluppare i principi dei meccanismi di visione artificiale.
Gli algoritmi usati nella corteccia per valutare la disparità stereoscopica non sono conosciuti, anche se sono state registrate dalla corteccia le caratteristiche delle risposte di certi elementi che valutano la disparità. Per esempio, Poggio (1984) ha descritto cinque tipi distinti di risposte alla disparità nei neuroni corticali dei primati. Molti algoritmi di corrispondenza stereoscopica sono in buon accordo con i dati di tipo neurofisiologico e psicofisico. La struttura chiave di gran parte di questi algoritmi è una griglia bidimensionale di elementi per la correlazione, che valutano la disparità come funzione dell'azimuth. Gli output di questi elementi indicano possibili corrispondenze a coppie, sul piano orizzontale, tra i dati delle due retine. La griglia contiene una dimensione spaziale aggiuntiva rispetto ai dati retinici e, di conseguenza, la stima iniziale degli elementi di correlazione può indicare molte corrispondenze false, oltre a quelle corrette. Il problema della corrispondenza stereoscopica sta nel determinare quali corrispondenze sono corrette per rinforzarle, e quali sono false per sopprimerle.
Vi sono due classi principali di algoritrni per la corrispondenza stereoscopica: gli algoritmi appartenenti alla prima classe filtrano preliminarmente l'input su scale spaziali multiple, in modo da ridurre la probabilità di corrispondenze false; quelli della seconda classe, invece, distinguono le corrispondenze false da quelle corrette usando delle interazioni cooperative su una singola scala spaziale. Il primo approccio funziona bene per le immagini standard, ma non è in grado di eguagliare le prestazioni degli esseri umani per le immagini in cui le componenti a bassa frequenza sono state eliminate. Il secondo approccio esprime la continuità degli oggetti attraverso una retro azione positiva tra elementi di correlazione vicini, che hanno una certa disparità. Questo algoritmo fallisce in caso di oggetti molto inclinati, che invece sono facilmente percepiti dagli esseri umani. Il chip di Mahowald per la corrispondenza stereoscopica combina questi due algoritmi per ottenere un modello più accurato della percezione umana.
La principale innovazione dell' algoritmo cooperativo multirisoluzione sta nell 'introduzione delle interazioni cooperative di retro azione tra le rappresentazioni di disparità a diverse scale spaziali. Esso funziona in maniera diversa dai tipici algoritrni multirisoluzione, che propagano l'informazione in una sola direzione (dalla codifica delle componenti a bassa frequenza alla codifica di quelle ad alta frequenza). Infatti, l'approccio cooperativo multirisoluzione genera una stima delle componenti a bassa frequenza spaziale della disparità partendo dall'output delle unità che corrispondono alle componenti ad alta frequenza. Il sistema, nel suo complesso, trasforma la codifica della disparità basata sui valori che la matrice di elementi di correlazione assume in una data posizione in una codifica analogica della disparità (Ballard, 1986).
Questo chip è in grado di fondere gli stereo grammi di punti casuali e di risolvere altri complicati problemi di corrispondenza stereoscopica, come la fusione di superfici molto inclinate. Esso mostra come una rete possa usare la retro azione positiva per effettuare un'elaborazione complessa, come l'eliminazione di false corrispondenze, rimanendo al tempo stesso sensibile all'input retinico. Questo chip è interessante dal punto di vista biologico, perché tratta la fusione stereoscopica come esempio di una classe generale di problemi, legati al rispetto di vincoli nella percezione sensoriale, e mostra come questa classe di problemi si possa risolvere utilizzando elementi neuromorfi.
Il tetto ottico
Le prestazioni in tempo reale dei sistemi neuromorfi suggeriscono che l'elettronica a VLSI possa essere uno strumento per sua natura privilegiato per l' emulazione dei processi di elaborazione che sono alla base delle funzioni comportamentali. Una di queste funzioni, che è stata ampiamente studiata nei sistemi biologici e fa da complemento ai sistemi a VLSI sopra descritti, è il controllo dei movimenti dell' occhio. Il movimento dell' occhio permette al sistema visivo di cercare attivamente nuovi dati sulla base dei dati precedentemente acquisiti. Con tale funzione, il carattere dei processi sensoriali da passivo diventa attivo (Ballard, 1991).
Il primo passo verso la realizzazione di un sistema di controllo oculare aVLSl è stato compiuto da S.P. DeWeerth (1992), per mezzo della costruzione di un primitivo sistema di movimento del tetto ottico per seguire il 'baricentro' luminoso di un'immagine. In questo sistema l'input visivo viene fornito da una retina bidimensionale, con un circuito di aggregazione che calcola il 'baricentro' di luminosità lungo le dimensioni orizzontale e verticale. L'ampiezza dei segnali visivi di input viene normalizzata prima che i segnali siano aggregati. Ciò serve a impedire che i cambiamenti nell'illuminazione globale influenzino la localizzazione del 'baricentro'. Il collicolo superiore impiega un principio di elaborazione simile per integrare l'informazione visiva per il controllo del movimento dell'occhio (Sparks e Mays, 1990).
Il sistema di movimento del tetto ottico converte l' output dello stadio di elaborazione del 'baricentro' in un segnale motorio, e usa questo segnale per aggiornare la posizione della retina. Le correnti di output aggregate sono poi convertite in treni di impulsi, che vengono direttamente impiegati per guidare dei motori 'antagonisti' che spingono in direzioni opposte in un sistema meccanico bidirezionale. Questi motori, che svolgono il ruolo dei muscoli oculari, sono posizionati in una configurazione tale da produrre delle forze di torsione, che tendono a orientare l'occhio in direzioni opposte. Ogni impulso in uscita dal chip controlla uno dei motori. Se il chip viene stimolato da una sorgente luminosa che non si trova al centro della griglia di fotorecettori, i motori producono una forza di torsione differenziale, che ruota l'occhio in modo da far muovere il centro della griglia verso lo stimolo. Quando lo stimolo proviene dal centro, ciascuno dei motori produce una forza di torsione uguale e opposta, a causa degli impulsi emessi spontaneamente dai circuiti neuronali. Il sistema meccanico genera una retro azione negativa per spostare il chip della retina, in modo che esso si trovi sempre di fronte allo stimolo.
Movimenti saccadici dell'occhio
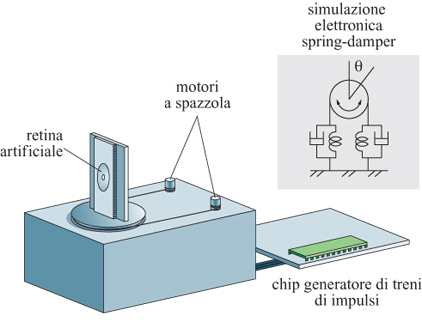
T. Horiuchi (1997) ha proposto un sistema a VLSI per il movimento del tetto ottico più raffinato, che riproduce i movimenti saccadici dell'occhio e l'inseguimento progressivo degli oggetti (fig. 13). Il modello di Horiuchi utilizza una retina unidimensionale che lavora in tensione per rivelare i cambiamenti temporali della luminosità all'interno del campo visivo del chip. Se questi cambiamenti avvengono nelle aree periferiche della retina (ovvero al di fuori di una finestra di dimensioni assegnate, centrata sulla griglia dell'immagine), provocano un movimento saccadico di risposta e attivano un chip, il quale genera una raffica di impulsi e controlla dei motori elettrici a spazzola (chiudendo così il cerchio di retroazione). D'altra parte, se i cambiamenti di luminosità temporale sono vicini al centro della retina, il sistema inizia un inseguimento progressivo. L'inseguimento progressivo ha due caratteristiche principali: esso viene controllato da stimoli visivi e dipende dalla velocità dell'oggetto da inseguire. Nel suo sistema, Horiuchi integra il segnale che viene dal chip della retina sul moto dell'oggetto da inseguire (accelerazione dell'occhio). Il segnale integrato risultante è la velocità dell' occhio e viene utilizzato per controllare il chip generatore delle raffiche di impulsi (v. figura 13). La modalità di ricerca con movimenti saccadici e quella di ricerca progressiva operano in parallelo, permettendo al sistema di inseguire in modo affidabile oggetti in movimento con velocità variabile. Il comportamento del sistema riproduce in modo assai soddisfacente i dati ottenuti da esperimenti sul movimento degli occhi compiuti sui primati. Il modello di Horiuchi è un buon esempio di un sistema neuromorfo con retro azione caratterizzato da un'interazione motoria e sensoriale con l'ambiente naturale.
La guida di veicoli
Si possono costruire interessanti sistemi, capaci di interagire in tempo reale con un ambiente naturale, collegando dei sensori neuromorfi a dispositivi digitali tradizionali. Uno dei primi sistemi a integrare la tecnologia digitale con dispositivi a VLSI neuromorfi è stato descritto da G. lndiveri e P. Verschure (1997). Questo sistema comprende una retina unidimensionale che lavora in corrente, una piattaforma mobile controllata da un microprocessore con un Mbyte di memoria RAM e dell'elettronica di supporto aggiuntiva. La retina analogica di silicio a bassa potenza fornisce al robot una preelaborazione dell'informazione sensoriale veloce, parallela e a basso costo. Un algoritmo di controllo, programmato sulla CPU del robot, usa i dati elaborati dalla retina di silicio per svolgere il compito di seguire una linea. Nonostante la semplicità del meccanismo di controllo (non contiene nessuna strategia di ricerca sofisticata per individuare i bordi delle figure, né alcun filtro temporale per stimare la loro possibile posizione futura sulla base dei dati acquisiti), il sistema si è mostrato in grado di svolgere in modo affidabile il suo compito, operando su figure immerse in un ambiente reale, in condizioni variabili di illummazione. Le capacità del sensore neuromorfo di preelaborare il segnale visivo in tempo reale sono usate per permettere al sistema di seguire un bordo continuo in modo autonomo e affidabile. Il compito più gravoso dal punto di vista dell' elaborazione del segnale, cioè quello di estrarre dalla scena visiva le caratteristiche rilevanti, viene svolto senza sforzo dal dispositivo a VLSI, lasciando le risorse della CPU libere per altri compiti di elaborazione.
Conclusioni
Nel corso degli anni Novanta l'elettronica dei transistor CMOS (Complementary Metal Oxide Semiconductor, semiconduttore complementare a ossido di metallo) a VLSI è stata usata per costruire una grande varietà di dispositivi neurali, da singole sinapsi, a griglie di sensori, fino a semplici sistemi neuromorfi. Questi circuiti non sono elaboratori di carattere generale, ma semplicemente sfruttano la fisica dei transistor analogici per produrre l'elaborazione necessaria a svolgere un compito specifico.
I circuiti analogici hanno il vantaggio di imitare i sistemi biologici in tempo reale. Nella misura in cui la fisica dei transistor soddisfa le necessità dell'elaborazione che deve essere svolta e la comunicazione digitale tra chip è ridotta, i circuiti a VLSI consumano meno energia e necessitano di una minore area di silicio rispetto agli equivalenti digitali. Questo è un importante vantaggio, perché ogni tentativo serio di riprodurre la potenza di elaborazione del cervello deve sfruttare le risorse nel modo più efficiente possibile. Il cervello svolge circa 10¹⁶ operazioni al secondo. Usando la migliore tecnologia digitale che si possa immaginare, per ottenere queste prestazioni sarebbe necessario dissipare più di 10 MW di potenza (Mead, 1990), contro i pochi watt consumati dal cervello. Anche le prestazioni dei circuiti a VLSI sotto soglia non sono comparabili a quelle dei circuiti neuronali, ma i consumi sono quattro ordini di grandezza inferiori rispetto a quelli della controparte digitale.
La natura specializzata ma efficiente dei sistemi neuromorfi prefigura per l'emulazione analogica un ruolo diverso da quello della simulazione digitale nell'indagine sui sistemi biologici. L'emulazione analogica è particolarmente utile per legare le proprietà fisiche del sistema alle sue funzioni di elaborazione, perché entrambi i livelli di astrazione sono combinati nello stesso sistema. In molti casi i sistemi analogici neuromorfi fanno uso diretto della fisica dei dispositivi per riprodurre i processi di elaborazione dei neuroni, e quindi il livello di base dell'analisi è intrinsecamente legato alla macchina stessa. Poiché l'elaborazione dei segnali avviene tramite un processo fisico, è relativamente facile passare dall'emulazione alla predizione fisiologica.
Ringraziamenti
Ringraziamo i partecipanti al congresso Telluride workshop on neuromorphic engineering per le molte e utili discussioni. La preparazione di questo saggio è stata sovvenzionata dalla Swiss National Science Foundation SPP Grant e dallo U. S. Office of Naval Research.
Bibliografia citata
BALLARD, D.H. (1986) Cortical connections and parallel processing: structure and fnnction. Behav. Brain Sci., 9, 67-120.
BALLARD, D.H. (1991) Animate vision. A.I., 48, 57-86.
BOAHEN, K.A. (1996) A retinomorphic visual system. IEEE Miero, 16, 30-39.
BOAHEN, K., ANDREOU, A. (1992) A contrast sensitive silicon retina with reciprocal synapses. In Advances in neural information processing systems, a c. di Touretzky D.S., Mozer M., Hasselmo M., San Mateo, Morgan Kaufmann, voI. 4.
DELBRÜK, T. (1993) Silicon retina with correlation-based, velocity-tnned pixels. IEEE Trans. Neural Networks, 4, 529-541.
DELBRÜK, T. (1994). Analog VLSI phototransduction by continuous-time, adaptive, logarithmic photoreceptor circuits. Technical report, Pasadena, California Institute of Technology, CNS Memo, 30.
DEWEERTH, S.P. (1992) Analog VLSI circuits for stimulus localization and centroid computation. Int. J. Comp. Vision, 8, 191-202.
DOUGLAS, R., MAHOWALD, M., MEAD, C. (1995) Neuromorphic analog VLSI. Annu. Rev. Neurosci., 18, 255-281.
EUAS, J.G. (1993) Artificial dendritic trees. Neural Comput., 5, 648-664.
HARRISON, R., KOCH, C. (1998) An analog VLSI model ofthe fly elementary motion detector. In Advances in neural information processing systems: Proceedings of the 1997 conference, voI. 10, a c. di Jordan I., Kearns M.J., Solla S.A., San Mateo, Morgan Kaufmann.
HORIUCHI, T. (1997) Analog VLSI-based, neuromorphic sensorimotor systems: modeling the primate oculomotor system. Ph. D. thesis, Department of Computation and Neural Systems, Pasadena, California Institute of Technology.
HORIUCHI, T., BAIR, W., BISHOFBERGER, B., MOORE, A., KOCH, C. (1992) Computing motion using analog VLSI vision chips: an experimental comparison among different approaches. Int. J. Comp. Vision, 8, 203-216.
HORIUCHI, T., LAZZARO, J.P., MOORE, A., KOCH, C. (1991) A delay-line based motion detection chip. In Advances in neural information processing systems, voI. 3, a c. di Lippman R., Moody J., Touretzky D.S., San Mateo, Morgan Kaufmann.
INDIVERI, G. (1997) Winner-take-all networks with lateral excitation. J. of Analog Integrated Circuits and Signal Processing, 13 (1/2), 185-193.
INDIVERI, G., KRAMER, J., KOCH, C. (1996) System implementations of analog VLSI velocity sensors. IEEE Miero, 16, 40-49.
INDIVERI, G., VERSCHURE, P. (1997) Autonomous vehicle guidance using analog VLSI neuromorphic sensors. In Artificial Neural Networks - ICANN'97, Lecture notes in computer science, Losanna, Springer Verlag, voI. 1327.
JOHNSTON, D., WU, S. (1995) Foundations of cellular neurophysiology. Cambridge, Mass., MIT Press.
JULESZ, B. (1971) Foundations of Cyclopean Perception. Chicago, University of Chicago Press.
KOCH, C. (1998) Biophysics of computation: information processing in single neurons. Oxford-New York, Oxford University Press.
KOCH, C., SEGEV, I. (1989) Methods in neuronal modelling: Jrom synapses to networks. Cambridge, Mass., MIT Press.
KRAMER, J., INDIVERI, G., KOCH, C. (1996) Analog VLSI motion projects at caltech. In Proc. Int. Symp. on Advanced Imaging and Network Technologies, Berlino.
KRAMER, J., SARPESHKAR, R., KOCH, C. (1997) Pulse-based analog VLSI velocity sensors. IEEE Trans. Circuits and Systems lI: Analog and Digital Signal Proc., 44, 86-101.
LAZZARO, J., WAWRZYNEK, J., MAHOWALD, M., SIVILOTTI, M., GILLESPIE, D. (1993) Silicon auditory processors as computer peripherals. IEEE Trans. Neural Networks, 4, 523-528.
LIU, S. (1996) Silicon model of motion adaptation in the fly visual system. In Proc. of Third Joint Caltech/UCSD Symposium, pp. 1-10.
MAHOWALD, M. (1992) VLSI analogs of neuronal visual processing: A synthesis of Jorm and Junction. Ph. D. thesis, Department of Computation and Neural Systems, Pasadena, Califorma Institute of Technology.
MAHOWALD, M. (1994) An analog VLSI system Jor stereoscopic vision. Boston, Kluwer.
MAHOWALD, M., DOUGLAS, R. (1991) A silicon neuron. Nature, 354, 515-518.
MAHOWALD, M., MEAD, C. (1989) Silicon retina. In Analog VLSI and neural systems, Reading, Addison-Wesley, pp. 257-278.
MARR, D. (1982) Vision: a computational investigation into the human rapresentation and processing of visual information, San Francisco, W.H. Freeman.
MEAD, C. (1990) Neuromorphic electronic systems. Proc. IEEE, 78, 1629-1636.
MURRAY, A.F. (1999) Pulse-based computation in VLSI neural networks. In Pulsed Neural Networks, a c. di Maass W., Bishop C.M., Cambridge, Mass., MIT Press, cap. A3.
NORTHMORE, D., EUAS, J. (1999) Dendritic tree neuromorphs: building blocks for silicon nervous systems. In Pulsed Neural Networks, a c. di Maass W., Bishop C.M., Cambridge, Mass., MIT Press, cap. B8.
POGGIO, G.T. (1984) Processing of stereoscopic inforrnation in primate visual cortex. In Dynamic aspects of neocortical function, a c. di Einar Gall W., Edelman G.M., Cowan W.M., New York, John Wiley & Sons, pp. 613-635.
POGGIO, G.T., VERRI, A., TORRE, V. (1991) Green theorems and qualitative properties of the optical flow. Technical report, MIT. InternaI Lab. Memo 1289.
RASCHE, C., DOUGLAS, R., MAHOWALD, M. (1998). Characterization of a pyramidal silicon neuron. In Neuromorphic Systems Engineering Silicon from Neurobiology, a c. di Smith L.S., Hamilton A., Singapore-River Edge, World Scientific.
SPARKS, D., MAYS, L. (1990) Signal transforrnations required for the generation of saccadic eye movements. Annu. Rev. Neurosci., 13, 309-336.
TRAUB, R.D., MILES, R. (1991) Neuronal networks oJthe hippocampus. Cambridge-New York, Cambridge University Press.