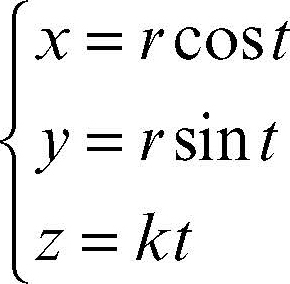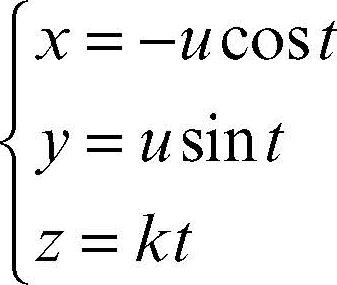elicoide

elicoide

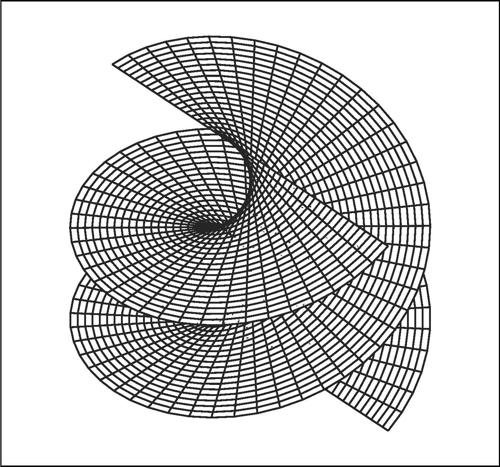
elicoide superficie rigata generata da una retta che si muove nello spazio con un moto elicoidale uniforme (composto di un moto uniforme di rotazione intorno a un asse fisso e di un moto di traslazione uniforme parallelo all’asse stesso) e i cui punti descrivono eliche. All’elicoide appartengono infinite eliche circolari di uguale asse, passo e verso. La più semplice delle superfici elicoidali è l’elicoide rigato chiuso generato da una retta che si muove nello spazio appoggiandosi da una parte a un’elica cilindrica e dall’altra all’asse di questa in modo da formare un angolo costante α con il piano perpendicolare all’asse. Se in un riferimento cartesiano Oxyz l’elica ha equazioni parametriche

allora l’elicoide retto e chiuso, la cui generatrice si appoggia sull’asse Oz, ha equazioni

Nell’elicoide retto, la retta è perpendicolare all’asse dell’elica; esso risulta una superficie minima (si veda → Plateau, problema di) e corrisponde, in pratica, alla superficie della scala a chiocciola e della vite a filetto rettangolare immaginate come prolungate indefinitamente. Tra gli elicoidi cerchiati (generati cioè dal moto elicoidale di un cerchio) si ricorda, per esempio, la colonna tortile, che è l’elicoide generato da un cerchio giacente in un piano perpendicolare all’asse. Un elicoide è una superficie invariante per tutte le isometrie composte da una traslazione lungo l’asse e una rotazione intorno all’asse, i cui parametri stanno in un dato rapporto.