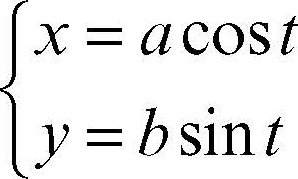ellisse

ellisse

ellisse curva piana chiusa, non intrecciata, priva di punti all’infinito; può essere ottenuta come luogo dei punti del piano tali che la somma delle loro distanze da due punti fissi, detti fuochi, risulti costante, o equivalentemente come luogo dei punti del piano le cui distanze da un punto fisso detto → fuoco e da una retta fissa detta direttrice sono in un rapporto costante e < 1. La costante e è detta eccentricità dell’ellisse e, nel caso particolare in cui assume valore zero, l’ellisse è una circonferenza, nel cui centro coincidono i due fuochi. Insieme a iperbole e parabola, l’ellisse è una → conica perché può essere ottenuta come sezione intersecando la superficie di un cono circolare indefinito con un piano che forma con l’asse del cono un angolo minore della sua apertura incontrando tutte le generatrici. In coordinate cartesiane l’equazione dell’ellisse è

con

Assumendo come origine di un sistema cartesiano ortogonale il centro di simmetria dell’ellisse (sulla retta per i fuochi ed equidistante da essi), come asse delle ascisse l’asse focale, cioè la retta per i due fuochi F(c, 0) e F′ (−c, 0), con c > 0, come asse delle ordinate l’asse del segmento F′F e come somma delle distanze di un generico punto P dai due fuochi la costante 2a, la sua equazione cartesiana assume la forma

avendo posto b² = a² − c². Tale equazione (equazione canonica dell’ellisse) è equivalente alla seguente forma parametrica:

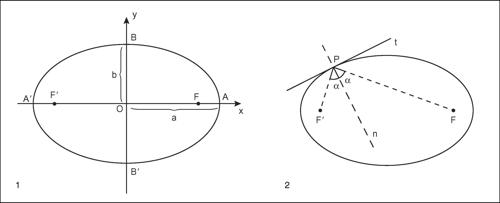
Con riferimento alla figura, le rette dei segmenti AA′ e BB′ sono detti, rispettivamente, asse maggiore e asse minore, mentre l’origine O è detta centro dell’ellisse. I valori a e b (positivi) rappresentano, rispettivamente, le misure del semiasse maggiore e del semiasse minore, mentre l’eccentricità è data da e = c /a. Ogni corda passante per O è detta diametro dell’ellisse. In un riferimento polare avente uno dei fuochi come origine e come asse polare l’asse focale orientato verso il vertice più vicino, l’equazione dell’ellisse si scrive nella forma ρ = p/(1 + ecosθ) in cui p (parametro dell’ellisse) è la metà della lunghezza della corda passante per un fuoco e perpendicolare all’asse focale. L’area racchiusa da un’ellisse di semidiametri a e b è A = πab.

La costruzione di un’ellisse può essere eseguita con differenti metodi; tra i più semplici e noti è il cosiddetto metodo del giardiniere utilizzato per tracciare un’aiola ellittica. Il metodo consiste nel piantare sul terreno due pioli, i fuochi, ai quali si legano gli estremi di una corda inestensibile la cui lunghezza supera la distanza tra i due fuochi. Con un paletto appuntito, che scorre all’interno della corda tesa e mantenuto in posizione verticale rispetto al suolo, si traccia sul terreno una linea ellittica. Un’importante proprietà di questa curva, anche per le sue applicazioni, è la cosiddetta proprietà focale dell’’ellisse, che può essere così formulata: in ogni punto P di un’ellisse, la bisettrice dell’angolo

è perpendicolare alla tangente in P alla curva. Ciò vuol dire, per esempio, in termini ottici, che in uno specchio avente forma ellittica, tutti i raggi di luce uscenti da una sorgente puntiforme situata in uno dei suoi fuochi, si riflettono passando tutti per l’altro fuoco.