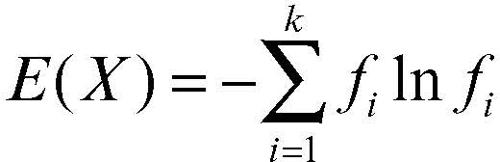entropia

entropia

entropia termine mutuato dalla fisica e utilizzato con significato leggermente diverso sia in teoria dell’informazione, dove fu introdotto da C. Shannon nel 1949, sia in probabilità e statistica.

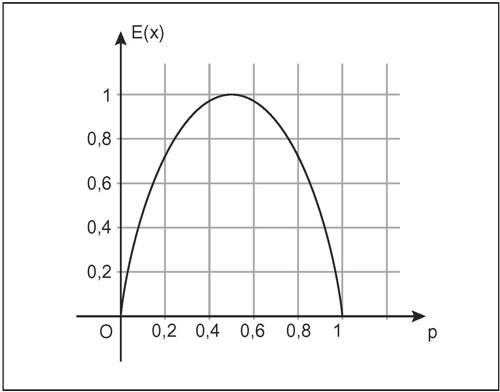
☐ In teoria dell’informazione, indice che misura la quantità di informazione prodotta da una sorgente. L’indice è funzione della distribuzione di probabilità dei segnali che può emettere la sorgente stessa. Se la sorgente è di tipo binario, come di fatto lo sono quelle digitali, può emettere soltanto una successione di bit, indicati convenzionalmente con 0 o 1. In tale caso, la quantità di informazione è tanto maggiore quanto più imprevedibile è tale successione di bit: in altre parole, se il segnale emette sequenze predeterminate a bassa probabilità, per esempio di tutti 0 o tutti 1, l’informazione è nulla; l’informazione è invece massima quando la sorgente emette una particolare sequenza tra altre di uguale probabilità. A partire da queste considerazioni, si costruisce una funzione della variabile aleatoria X, detta entropia, che dipende dalle probabilità dei due eventi disgiunti P(X = 0) = p e P(X = 0) = 1 − p, e che assume il valore 0 quando p = 0 o p = 1 e il valore massimo 1 quando p = 1/2.

Tale funzione è E(X) = −plog₂(p) − (1 − p)log₂(1 − p), il cui valore, tenendo conto che

si pone uguale a 0 quando p = 0 o p = 1. Generalizzando, se la sorgente è una variabile aleatoria con n possibili valori x₁, …, x_n, l’entropia di tale variabile è

che può anche scriversi come

avendo indicato con p(x_i) la probabilità P(X = x_i) che X assuma la modalità x_i.

☐ In statistica, indice che misura l’eterogeneità di una → distribuzione statistica. Un collettivo statistico è detto assolutamente omogeneo relativamente a un carattere se tutte le unità presentano un’unica modalità di quel carattere, cioè se una delle frequenze relative è uguale a 1 e tutte le altre sono nulle; si dice, invece, assolutamente eterogeneo se tutte le unità del collettivo sono ripartite in classi di modalità con uguale frequenza, se cioè sono equidistribuite: se k ≥ 2 è il numero delle modalità, in caso di assoluta eterogeneità le frequenze relative saranno allora: ƒ₁ = ƒ₂ = ... = ƒ _k = 1/k.

L’entropia del carattere X, con k distinte modalità, è allora così definita

dove In indica il logaritmo naturale. Anche in questo caso, tenendo conto che

si pone 0ln(0) = 0 e l’espressione risulta così definita anche nel caso di modalità con frequenza nulla. L’indice varia da 0, nel caso di assoluta omogeneità, a ln(k), nel caso di massima eterogeneità.

Una misura relativa di tale indice, in modo tale che il suo massimo non dipenda dal numero k delle classi, è

che varia da 0 a 1. Si può notare come, identificando frequenza e probabilità, la formalizzazione matematica dell’entropia sia di fatto la medesima in teoria dell’informazione e in statistica. L’indice è prevalentemente utilizzato nel caso di caratteri qualitativi, ma può essere esteso a ogni tipo di carattere. Nel caso di caratteri quantitativi, esso dà un’indicazione sulla → concentrazione, cioè sul modo in cui è ripartito un totale tra più unità e fornisce valori molto simili al relativo indice di Gini.