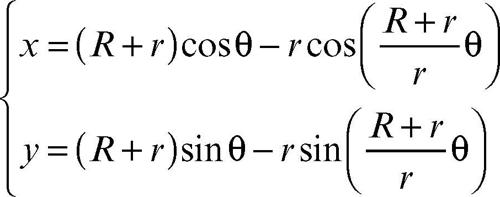epicicloide

Enciclopedia della Matematica (2013)

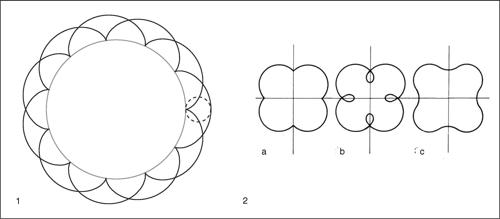
epicicloide


epicicloide curva descritta da un punto di una circonferenza che rotola, senza strisciare, su una seconda circonferenza fissa alla quale è tangente esternamente. In un riferimento cartesiano avente per origine il centro della circonferenza fissa, l’epicicloide ha equazioni parametriche

formula

dove r e R indicano, rispettivamente, il raggio della circonferenza mobile e il raggio della circonferenza fissa e il parametro θ è l’angolo formato con l’asse x dalla congiungente il punto della curva con l’origine. Se R = r, l’epicicloide presenta una sola cuspide ed è una → cardioide. Se R = 2r, l’epicicloide presenta due cuspidi ed è detta nefroide. Se R /r è un numero irrazionale, la curva non si chiude. Nei tre casi possibili di un punto solidale al cerchio mobile che sia interno, sul contorno o esterno al cerchio stesso, l’epicicloide si dice accorciata, ordinaria o allungata. Le curve che si ottengono considerando invece il moto di un cerchio che rotola senza strisciare internamente a una circonferenza si dicono → ipocicloidi.

EPICICLOIDE

Vedi anche
ipocicloide fig.La curva descritta da un punto P rigidamente collegato a un cerchio c (v. fig.), detto epiciclo, tangente internamente a un cerchio fisso k del suo piano e che rotoli senza strisciare su k. L’i. è ordinaria, accorciata o allungata a seconda che il punto P sia, rispettivamente, sul cerchio mobile, ... cicloide fig.Curva descritta da un punto rigidamente collegato a un cerchio K (epiciclo), che rotoli nel piano, senza strisciare, su una retta fissa s. Una c. (v. fig.) si dice: a) ordinaria, se il punto P giace sulla circonferenza di K; b) accorciata, se il punto P′, è interno a K; c) allungata, se il punto ... cardioide fig.Curva algebrica piana ottenuta a partire da una circonferenza di raggio a (v. fig.) e dal fascio di rette passanti per un suo punto O, staccando su ciascuna retta segmenti 2a da ambo le parti delle ulteriori intersezioni con la circonferenza stessa: (x2 + y2)2 − 4ax (x2 + y2) − 4a2y2 = 0. La c. appartiene ... cuspide anatomia Ciascun lembo delle valvole atrioventricolari del cuore. Ciascun rilievo o tubercolo ben visibile sulla superficie triturante dei premolari e dei molari: nei primi ( bicuspidati), in numero di due; nei secondi ( multicuspidati), in numero di quattro. Astronomia Ciascuna delle punte con cui ...
Tag
Vocabolario
epiciclòide
epicicloide epiciclòide agg. e s. f. [comp. di epi- e cicloide3]. – In geometria, curva e. (o assol. epicicloide), curva piana descritta da un punto rigidamente collegato a un cerchio che rotoli senza strisciare sopra un cerchio fisso del...
epicicloidale
epicicloidale agg. [der. di epicicloide]. – In geometria, moto e., moto rigido piano, generabile per rotolamento, senza strisciamento, di un cerchio su un altro (v. anche epicicloide).