epigrafo

epigrafo

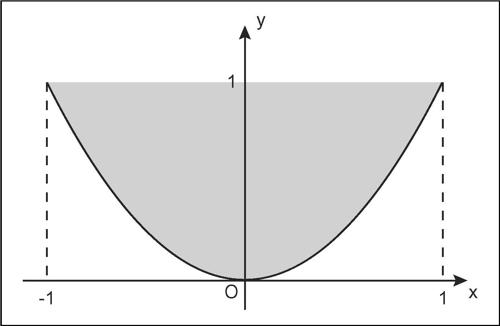
epigràfo riferito al grafico di una funzione y = ƒ(x), denota l’insieme dei punti del piano situati sul grafico o al di sopra di esso, cioè l’insieme dei punti (x, y) tali che y ≥ ƒ(x). Più in generale, data una funzione reale di n variabili reali, ƒ : A ⊆ Rⁿ → R, si dice epigràfo l’insieme dei punti dello spazio Rⁿ⁺¹ aventi come prime n coordinate quelle di un punto del dominio A della funzione e come (n + 1)-esima coordinata un numero reale maggiore o uguale al valore assunto dalla funzione in x_n. Se A è un insieme convesso, la funzione è convessa se e solo se tale è il suo epigràfo.