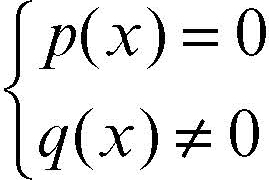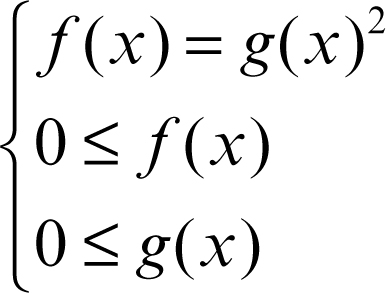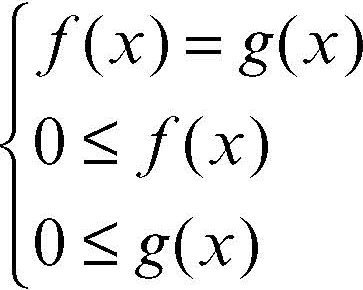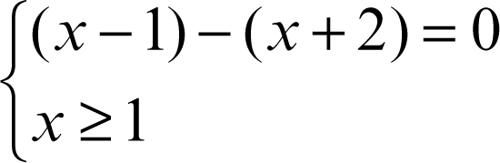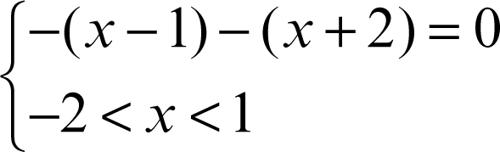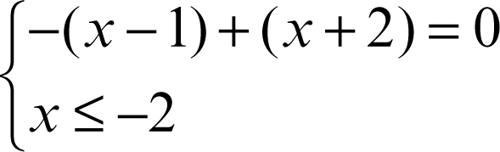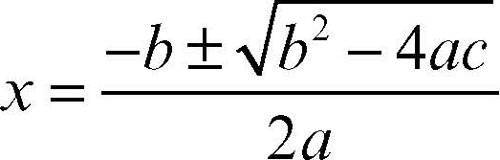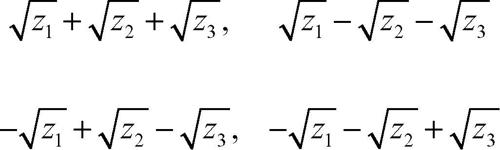equazione algebrica
equazione algebrica
equazione algebrica equazione che, eventualmente dopo opportune trasformazioni che utilizzano le proprietà dei numeri reali, assume forma polinomiale, cioè del tipo p(x1, …, xn) = 0, dove p è un polinomio di una o più variabili, oppure assume la forma di uno o più sistemi misti in cui compaiono equazioni in forma polinomiale.
Una equazione algebrica è detta intera se nessuna delle incognite compare mai al denominatore delle espressioni algebriche che la compongono; altrimenti essa è detta frazionaria o fratta. Una equazione è detta razionale se nessuna delle incognite compare come argomento di una radice, altrimenti è detta irrazionale. Si evidenziano così quattro possibili casi:
• equazioni razionali intere;
• equazioni razionali fratte;
• equazioni irrazionali intere;
• equazioni irrazionali fratte.
Equazione razionale
Una equazione razionale intera in una incognita può sempre essere ricondotta alla forma p(x) = 0, dove p è un polinomio nell’indeterminata x. Per le frazionarie, sempre limitandosi al caso di equazioni in una incognita, ci si riconduce sempre alla forma equivalente
in cui p(x) e q(x) sono due polinomi. Le sue soluzioni sono allora quelle del sistema misto equivalente:
Equazione irrazionale
Poiché nelle equazioni irrazionali una delle incognite compare come argomento di una radice, per risolvere in R una equazione di questo tipo si ricorre, in modo opportuno, all’elevazione a potenza. Se l’indice n della radice sotto cui compare l’incognita è dispari, allora la funzione di variabile reale xn è iniettiva e pertanto, elevando alla potenza n-esima ambo i membri dell’equazione, si ottiene un’equazione equivalente. Ciò è falso se invece l’indice n è pari: in questo caso, per risolvere l’equazione sull’insieme R dei numeri reali, bisogna imporre che il radicando non sia negativo affinché la radice sia definita; ci si riconduce dunque allo studio di un opportuno sistema misto di equazioni e disequazioni. Analizzando più in dettaglio il caso quadratico, si distinguono tre particolari situazioni notevoli, cui talvolta ci si può ricondurre partendo da un’arbitraria equazione irrazionale in cui l’incognita compare nell’argomento di una radice quadrata. Un’analoga casistica sarà valida nel caso di radici con un arbitrario indice pari:
l’equazione è equivalente all’equazione ƒ(x) = 0;
l’equazione è equivalente al sistema misto
l’equazione è equivalente al sistema misto
Risulta così evidente che nel caso di equazioni irrazionali fratte ci si riconduce a più espressioni frazionarie del tipo
e a un opportuno insieme di condizioni. Questo metodo risolutivo si applica in realtà anche a equazioni trascendenti irrazionali, anche se in tal caso non si giunge direttamente a equazioni polinomiali, ma a equazioni che è possibile trasformare in equazioni polinomiali con opportune sostituzioni.
Risolubilità di un’equazione algebrica
Il problema di risolvere una equazione frazionaria, così come quello di risolvere altri tipi di equazioni algebriche, rimanda quindi a quello di risolvere equazioni in forma polinomiale. Per tale motivo, la locuzione equazione algebrica è considerata spesso un sinonimo di equazione polinomiale. Il grado del polinomio è detto grado dell’equazione. La sua risoluzione equivale alla determinazione degli zeri o radici del polinomio stesso e perciò le sue soluzioni sono anche dette radici.
Nel caso di un’equazione algebrica in un’incognita di grado n su R (o C), il caso basilare cui, sfruttando i principi di equivalenza, ci si può sempre ricondurre è quindi quello di un’equazione del tipo
dove gli ak sono coefficienti numerici, detti coefficienti dell’equazione, con a0 ≠ 0. L’equazione letterale precedente è detta equazione generale di grado n (in un’incognita): essa è il prototipo di ogni equazione algebrica in un’incognita di grado n. Se si cercano soluzioni nel campo dei numeri complessi di una siffatta equazione, vale allora il teorema fondamentale dell’algebra, secondo il quale ogni polinomio di grado n ≥ 1 ammette esattamente n radici, contate con la relativa molteplicità: si dice che una radice α ha molteplicità m ≤ n se m radici dell’equazione coincidono con α. In generale, un numero α è una radice di un’equazione algebrica del tipo p(x) = 0 se e solo se il polinomio x − α divide p(x) (→ Ruffini, teorema di): pertanto una radice α ha molteplicità m se e solo se m è il massimo intero per cui il polinomio (x − α)m divide p(x).
Un’equazione algebrica di grado n in un’incognita si dice risolubile per radicali se è possibile ricavare tutte le sue n radici mediante un numero finito di operazioni di somma, prodotto, divisione, sottrazione ed estrazione di radice (con indice arbitrario) effettuate sui coefficienti dell’equazione. Se il grado dell’equazione è minore o uguale a 4, un’equazione algebrica in un’incognita è sempre risolubile per radicali: questo è il caso delle equazioni di primo grado (dette anche lineari), delle equazioni di secondo grado (dette anche quadratiche), delle equazioni di terzo grado (dette anche cubiche) e delle equazioni di quarto grado (dette anche quartiche), per le quali è possibile determinare una formula che esprima le radici dell’equazione generale mediante un numero finito di operazioni aritmetiche e di estrazioni di radice eseguite sui coefficienti. Se invece il grado dell’equazione è maggiore di 4, allora l’equazione generale in un’incognita non è risolubile per radicali: è questo il fondamentale teorema di → Abel-Ruffini. Ciò non vuol dire tuttavia che non esistano equazioni algebriche in un’incognita di grado superiore al quarto che siano risolubili per radicali: particolari casi di questo tipo sono le equazione binomie e le equazioni biquadratiche.
Diverse proprietà, di notevole interesse applicativo, delle radici di un’equazione algebrica in un’incognita possono essere stabilite anche senza il loro calcolo esplicito, come per esempio l’esistenza di radici reali (→ Cartesio, regola di; → Sturm, teorema di) o l’esistenza di sole radici con parte reale negativa (→ Routh-Hurwitz, teorema di). Un’equazione algebrica in una o più variabili si dice diofantea se è a coefficienti interi e di essa interessano le (eventuali) soluzioni intere (→ equazione diofantea).
Equazione binomia
Equazione algebrica in un’incognita della forma axn − b = 0. Essa è sempre risolubile per radicali in C: le sue soluzioni complesse sono le radici n-esime di b /a.
Equazione biquadratica
Equazione algebrica in un’incognita della forma ax 4 + bx 2 + c = 0.
Tale equazione può essere risolta attraverso la sostituzione y = x 2 e riconducendosi in questo modo all’equazione quadratica
Se y1 e y2 sono le due radici (eventualmente complesse) di quest’ultima, allora le quattro radici (eventualmente complesse) dell’equazione biquadratica considerata saranno
Equazione con valore assoluto
Equazione algebrica in cui un’incognita compare all’interno di un’espressione scritta in valore assoluto (più propriamente detto modulo nel caso in cui il dominio è C). Nel caso di un’equazione in un’incognita reale, per ricondursi a un’equazione senza valore assoluto, si scompone il dominio in intervalli in modo tale che tutti gli argomenti dei singoli moduli che compaiono nell’equazione abbiano segno costante su ciascun intervallo. In questo modo, applicando la definizione di valore assoluto, è possibile riscrivere l’equazione su ciascun intervallo in modo che non compaia nessun modulo e ci si riconduce allo studio di un sistema misto di equazioni e disequazioni senza valore assoluto. Per esempio, l’equazione |x − 1| − |x + 2| = 0 viene ricondotta, secondo quanto detto, allo studio separato dei tre sistemi misti
(caso in cui gli argomenti dei moduli sono entrambi positivi o nulli)
(caso in cui gli argomenti dei moduli sono uno negativo e uno positivo)
(caso in cui gli argomenti dei moduli sono entrambi negativi o nulli). Poiché i sistemi in (a) e (c) sono impossibili, le soluzioni dell’equazione coincidono con le soluzioni del sistema (b), il quale ha l’unica soluzione x = − 1/2. Occorre osservare che non c’è relazione immediata tra il grado dei polinomi che compaiono in tali equazioni e il numero delle soluzioni; per esempio, in R, l’equazione |x| = 1 ha come soluzioni −1 e +1.
Equazione cubica
Equazione algebrica di terzo grado. L’equazione generale cubica in un’incognita ha la forma ax 3 + bx 2 + cx + d = 0. Tale equazione è risolubile per radicali ed è possibile determinarne una formula risolutiva (→ Cardano, formule di) che ne esprima le radici (eventualmente complesse) in funzione dei coefficienti a, b, c e d.
Equazione lineare
È un’equazione algebrica di primo grado. Indipendentemente dal numero delle variabili, è un tipo di equazione sempre risolubile applicando i principi di equivalenza. L’equazione generale lineare in un’incognita ax + b = 0, con a ≠ 0, ha soluzione x = − b /a.
Equazione omogenea
Un’equazione algebrica si dice omogenea se è equivalente all’equazione ottenuta uguagliando a zero un polinomio senza termini costanti; ha quindi la forma a0xn + a1xn−1 + ... + an−1x = 0. Un’equazione omogenea ha sempre la soluzione banale x = 0 (se questo valore appartiene al dominio in cui l’equazione è definita).
Equazione quadratica
È un’equazione algebrica di secondo grado. L’equazione generale quadratica in un’incognita è ax 2 + bx + c = 0. Essa è risolubile per radicali e ha le due soluzioni
dove Δ = b2 − 4ac è il discriminante del polinomio ax 2 + bx + c: se Δ > 0 allora le due radici sono reali e distinte, se Δ = 0 allora esiste un’unica radice reale con molteplicità 2, se Δ < 0 allora le due radici sono complesse e coniugate. In modo compatto, le soluzioni dell’equazione di secondo grado in un’incognita sono fornite dalla formula risolutiva
Talvolta è possibile ridurre l’equazione alla forma x 2 + px + q = 0, con p pari e la formula risolutiva diventa
In questa forma, p rappresenta la somma delle radici cambiata di segno; q il loro prodotto.
Quando a, b, c (oppure p e q) sono razionali, le radici saranno numeri razionali soltanto se Δ è un quadrato perfetto. Se nell’equazione ax 2 + bx + c = 0 il coefficiente b è nullo, l’equazione è detta pura e ha come radici
se invece è nullo il termine noto c, l’equazione è detta spuria e ha come radici x = 0, x = –bla; se sono nulli b e c, l’equazione ha per radice doppia lo zero.
Equazione quartica
È un’equazione algebrica di quarto grado. L’equazione generale quartica in un’incognita ha la forma ax 4 + bx 3 + cx 2 + dx + e = 0.
Essa è risolubile per radicali: mediante la sostituzione
assume la forma y 4 +py 2 + qy + r = 0, le cui radici sono espresse dalle rispettive metà delle espressioni
dove z1, z2, z3 sono le soluzioni dell’equazione risolvente
Il primo esempio di formula risolutiva per l’equazione generale di quarto grado è stato fornito nel xvi secolo dal matematico L. Ferrari (→ Ferrari, formule di); tali formule differiscono leggermente da quelle in uso oggi.
Equazione reciproca
Un’equazione algebrica in un’incognita della forma
si dice reciproca se, supposto che α sia sua radice, allora anche il reciproco 1/α lo è. Ciò equivale a richiedere che i coefficienti ai e an-i equidistanti dagli estremi siano uguali (nel qual caso l’equazione reciproca viene detta di prima specie) o siano l’uno l’opposto dell’altro (nel qual caso l’equazione reciproca viene detta di seconda specie).
Equazione trinomia
È un’equazione algebrica in un’incognita della forma
Similmente al caso delle equazione biquadratiche, che le equazione trinomie generalizzano, la risoluzione di una tale equazione è strettamente legata a quella dell’equazione quadratica associata che si ottiene con la sostituzione y = xn
se y1 e y2 sono le due soluzioni (eventualmente complesse) di quest’ultima, allora l’insieme delle soluzioni (eventualmente complesse) dell’equazione biquadratica considerata è l’unione degli insiemi delle radici n-esime di y1, e di y2.