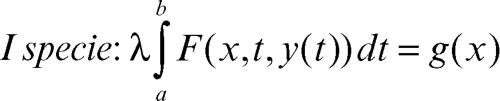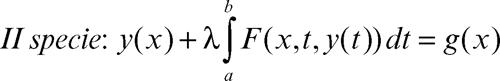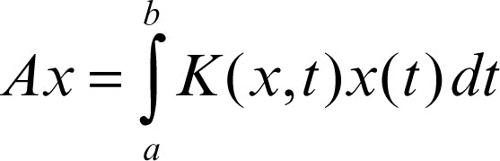Fredholm, equazione di
Fredholm, equazione di
Fredholm, equazione di equazione integrale lineare in cui gli estremi di integrazione sono fissi (a differenza delle equazioni di → Volterra). A seconda che l’equazione sia di prima o di seconda specie (→ equazione integrale) l’equazione di Fredholm ha rispettivamente una delle due seguenti forme:
L’equazione di prima specie può non avere soluzione per ogni scelta del secondo membro. Nel caso lineare la funzione F ha la forma F(x, t, y) = K(x, t)y, ove la funzione K si dice nucleo. Per l’equazione di seconda specie, sotto opportune ipotesi, vale l’alternativa: l’equazione ha una e una sola soluzione per ogni g oppure l’equazione omogenea associata (g(x) = 0 per ogni x) ha una soluzione non nulla.
Nel caso particolare di nucleo simmetrico (cioè K(x, t) = K(t, x)) se l’unità è un autovalore dell’operatore:
l’equazione ha soluzione se e solo se la funzione g è ortogonale a tutti gli autovettori di A associati all’autovalore 1: in tal caso l’equazione ha infinite soluzioni. Nel caso di nucleo degenere, della forma
la risoluzione si riduce a quella di un sistema di equazioni algebriche lineari.