equazione di Gelfand-Levitan-Marcenko (GLM)
Equazione di Gelfand-Levitan-Marcenko (GLM)
Equazione centrale nella risoluzione del problema inverso della diffusione nell’ambito della meccanica quantistica non relativistica, ossia nella risoluzione del cosiddetto problema spettrale inverso. La risoluzione di tale problema, e dunque la stessa equazione GLM, gioca un importante ruolo anche nello studio di alcune equazioni di evoluzione alle derivate parziali integrabili, quali, per es., la equazione di Korteweg-de Vries (equazione KdV). Il problema diretto della diffusione si basa sulla equazione (stazionaria) di Schrödinger, che in opportune unità di misura (e nel contesto di uno spazio unidimensionale) si scrive
e con −∞〈x〈+∞. In questa equazione di base del problema spettrale diretto la funzione reale u(x) è assegnata (e per ipotesi si annulla abbastanza rapidamente per x→±∞), il numero reale k2 è l’autovalore e alla autofunzione ψ(x,k) (soluzione di questa equazione differenziale) si richiede di mantenersi limitata per ogni valore della variabile spaziale x (anche nel limite in cui x→±∞). Pertanto – tenuto conto della proprietà della funzione u(x) di annullarsi asintoticamente – lo spettro degli autovalori k2 ha due componenti: tutti i valori positivi, k2>0, ed eventualmente un numero finito di valori negativi, k2=−p2ν, n=1,…,N. Agli autovalori positivi, cui corrisponde un valore reale (positivo) di k, si associano autofunzioni caratterizzate dal seguente comportamento asintotico:
[
]
per x→−∞;
[
]
per x→+∞. Queste formule identificano univocamente la corrispondente autofunzione ψ(x,k), nonché il coefficiente di trasmissione T(k) e il coefficiente di riflessione R(k). Agli autovalori negativi (qualora esistano) si associano invece autofunzioni ψ(x,ipν)=fν(x) normalizzabili, che devono dunque annullarsi per x→±∞ e che conviene caratterizzare univocamente mediante la condizione
[
]
cui si associa il coefficiente di normalizzazione
[
]
Il problema spettrale diretto consiste nella determinazione, data una funzione reale u(x), dei corrispondenti coefficienti di trasmissione T(k) e di riflessione R(k), del numero N di autovalori discreti – numero che potrebbe anche esser nullo, anzi lo sarebbe certamente se u(x)≥0 per −∞〈x〈+∞ – e delle corrispondenti quantità (positive) pν,ϱν, n=1,…,N. In particolare si definisce trasformata spettrale della funzione u(x) l’insieme di dati
La giustificazione per questa definizione della trasformata spettrale nasce dal fatto che i dati in essa contenuti sono necessari e sufficienti a determinare univocamente la corrispondente funzione u(x): la sua individuazione a partire dalla trasformata spettrale costituisce per l’appunto il problema spettrale inverso, nel cui ambito l’equazione integrale GLM gioca un ruolo essenziale. Data infatti la trasformata spettrale [4], si definisce una funzione
1
e l’equazione GLM si scrive allora come segue:
Questa equazione integrale di Fredholm – nella quale la funzione M(x) entra sia come termine noto che come nucleo – determina univocamente la funzione K(x,y) e questa determina a sua volta la funzione u(x) tramite la formula
→ Solitoni

![[1]](https://images.treccani.it/ext-tool/intra/thumbs_medium/9/92/VOL_6_equazione_gelfand_01.jpg)
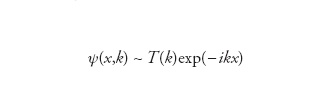
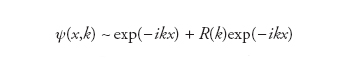
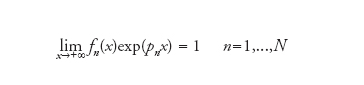
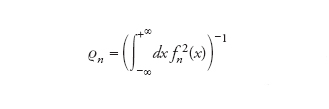
![[4]](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/fb/VOL_6_equazione_gelfand_04.jpg)
![[5]](https://images.treccani.it/ext-tool/intra/thumbs_medium/7/7e/VOL_6_equazione_gelfand_05.jpg)
![[6]](https://images.treccani.it/ext-tool/intra/thumbs_medium/9/9f/VOL_6_equazione_gelfand_06.jpg)
![[7]](https://images.treccani.it/ext-tool/intra/thumbs_medium/f/f2/VOL_6_equazione_gelfand_07.jpg)