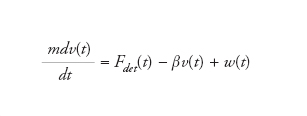equazione di Langevin
equazione di Langevin
Equazione differenziale stocastica in grado di descrivere il fenomeno della diffusione di particelle in un mezzo. Il moto che ne risulta, noto come moto browniano, rappresenta il moto effettuato da una particella semimacroscopica o mesoscopica (delle dimensioni cioè del micrometro), immersa in un fluido in equilibrio e soggetta agli urti con le molecole del mezzo. Se la velocità iniziale della particella browniana è diversa da zero, il numero di urti in direzione contraria al moto tende a diminuire la sua velocità (fenomeno viscoso o frizione). Se si approssima il fluido molecolare come un continuo che esercita sulla particella una forza di intensità e direzione aleatorie, dovuta agli urti con le molecole a livello microscopico, l’equazione di Langevin può scriversi
dove Fδετ(t) rappresenta le forze deterministiche (per es., l’interazione tra due particelle mesoscopiche dovuta alle forze intermolecolari e intramolecolari), βv(t) rappresenta l’attrito e w(t) è una forza aleatoria, di cui è nota soltanto la distribuzione di probabilità. Più in generale, w(t) è un processo stocastico, ovvero una famiglia di variabili casuali dipendenti dal tempo. Sotto opportune condizioni, il processo w(t) è detto processo di Wiener. Integrando l’equazione di Langevin si ottiene la legge del moto, ovvero la coppia data da posizione e velocità della particella. Anche la legge del moto è un processo stocastico, spesso chiamato processo di Ornstein-Uhlenbeck. L’equazione di Langevin rappresenta un buon modello per molti processi di tipo browniano (per es., il rumore termico nei componenti elettrici). La soluzione può essere ottenuta analiticamente mediante il metodo di Fokker-Planck oppure numericamente attraverso simulazioni Monte Carlo. L’equazione prende il nome da Paul Langevin, fisico francese che per primo studio il moto browniano in un potenziale di forze costante.
→ Simulazione di processi fisici mediante calcolatore