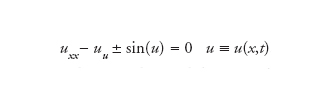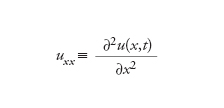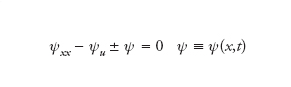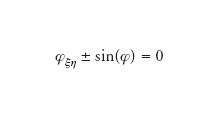equazione di seno-Gordon
equazione di seno-Gordon
È l’equazione non lineare alle derivate parziali del secondo ordine:
Qui e nel seguito le variabili sottoscritte indicano derivazioni parziali, per es.:
Agli inizi degli anni Settanta è stato dimostrato che questa equazione è ‘integrabile’, e questo è il principale motivo della sua importanza. Questa equazione nonlineare è inoltre invariante sotto trasformazioni di Lorentz, come l’analoga, ma lineare, equazione di Klein-Gordon
dalla quale l’equazione di seno-Gordon ha preso il nome, per ovvia assonanza. L’equazione di Klein-Gordon ha un importante ruolo nella meccanica quantistica relativistica. Anche l’equazione di seno-Gordon (che si riduce ovviamente all’equazione di Klein-Gordon nel limite in cui la variabile dipendente è piccola, u=εψ, ε→0) ha giocato e gioca un interessante ruolo in questo contesto, ma le sue applicazioni più importanti sono nella fisica dei solidi (in particolare nello studio dell’effetto Josephson) nonché nella geometria differenziale nel quale contesto alcune delle sue speciali proprietà (per es., le trasformazioni di Bäcklund a essa associate), connesse alla sua integrabilità, erano state già scoperte all’inizio del XX secolo. Inoltre la fenomenologia solitonica derivante dall’integrabilità dell’equazione di seno-Gordon è più ricca di quella associata all’equazione di Korteweg-de Vries, per es. per la presenza di componenti delle sue soluzioni interpretabili come stati legati di due solitoni, i cosiddetti breathers. Altre versioni dell’equazione di seno-Gordon si ottengono mediante i seguenti cambiamenti della variabile dipendente, u(x,t)=iν(x,t), rispettivamente u(x,t)=w(x,t)+π/2, che ovviamente generano analoghe versioni della stessa equazione di seno-Gordon in cui però la funzione seno viene è rimpiazzata dalla funzione seno iperbolico; nonché dal cambiamento delle variabili indipendenti u(x,t)=φ(ξ,η) – dalle coordinate di laboratorio (x,t) alle coordinate di cono luce ξ=(x+t)/2, η=(x−t)/2 – che la trasforma nell’equazione
→ Solitoni