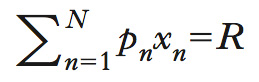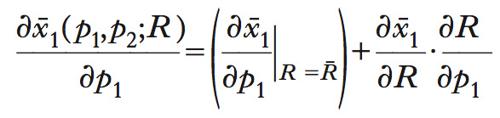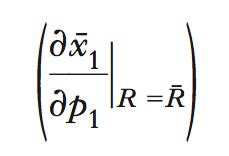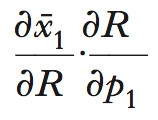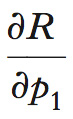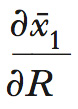Slutsky, equazione di
Slutsky, equazione di
Equazione che mostra gli effetti reddito e sostituzione prodotti sulla domanda da una variazione dei prezzi. In particolare, l’equazione di S. evidenzia il meccanismo matematico per il quale la domanda di beni di prima necessità e bassa qualità aumenta in seguito a un incremento del loro prezzo. Un po’ per esperienza e un po’ per ragionamento introspettivo, si dà per scontato che esista una relazione inversa fra la quantità domandata di un bene e il suo prezzo; a una crescita di questo viene cioè associata una diminuzione della disponibilità dei consumatori a comprare e quindi una riduzione della quantità domandata. In realtà, alla fine del 1800, l’economista e statistico scozzese R. Giffen (➔ anche Giffen, bene di) mise in luce la presenza di comportamenti che contrastavano con tale generale convincimento. La teoria del consumatore ipotizza che questi si comporti in modo razionale e determini le proprie scelte risolvendo un problema di massimizzazione della sua funzione di utilità U=U(x1,x2,...,xN), dove xn,(n=1,2,...,N) indica la quantità della merce n acquistata, soggetta al vincolo di bilancio
con pn pari al prezzo unitario della merce n ed R il reddito monetario, che si suppone esogenamente dato unitamente ai prezzi. Dalla soluzione di tale problema si ricavano le funzioni di domanda, che dipendono quindi dai prezzi di tutti i beni e dal reddito. Assumendo per semplicità che vi siano solamente due beni, è possibile quindi scrivere tali funzioni di domanda come x̄1(p1,p2;R) e x̄2(p1,p2;R). La teoria economica studia gli effetti delle variazioni delle variabili esogene sulle scelte del consumatore; in particolare, prende in esame le conseguenze della variazione del prezzo di un bene sulla domanda dello stesso. Si consideri l’ipotesi di un aumento di p1. A questa variazione corrisponde non solo un cambiamento del prezzo relativo dei due beni – il bene due è divenuto relativamente meno caro – ma anche un diverso potere d’acquisto del reddito monetario R, che risulta diminuito. L’equazione di S. consente di distinguere questi due aspetti, considerando separatamente l’effetto dovuto alla variazione del prezzo relativo, fermo restando il potere d’acquisto (effetto di sostituzione) e quello della variazione del potere d’acquisto (effetto di reddito).
In termini analitici, date le quantità domandate x̄1(p1,p2;R) e x̄2(p1,p2;R), si può dire che il potere d’acquisto del consumatore rimane costante se è in grado di comprare ai nuovi prezzi il paniere ottimale(x̄1,x̄2). Derivando totalmente rispetto a p1 la domanda, per es., del primo bene, si ottiene l’equazione di Slutsky
che illustra come la variazione della domanda sia data dalla somma algebrica di due termini: rispettivamente l’effetto di sostituzione e l’effetto di reddito. Il primo
è sempre negativo, dato che il consumatore sostituisce il bene divenuto più caro con quello relativamente più conveniente. Il segno dell’effetto di reddito
dipende dalle caratteristiche dei singoli beni: mentre la derivata
è certamente negativa (un aumento di p1 riduce il potere di acquisto), il segno della derivata
è positivo per un bene normale, ma negativo per uno inferiore. Si può pertanto concludere che un aumento del prezzo riduce la domanda di un prodotto normale, dato che gli effetti di sostituzione e di reddito sono entrambi negativi, mentre ha un impatto incerto sulla domanda di un bene inferiore, impatto che dipende dal peso relativo dell’effetto di reddito (in questo caso positivo) e dell’effetto di sostituzione (sempre negativo).
Un’analoga equazione di S. si ottiene seguendo l’impostazione di Hicks, che tiene costante il livello di utilità associato al paniere (x̄1,x̄2) anziché il potere d’acquisto.