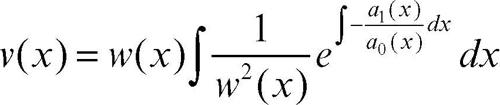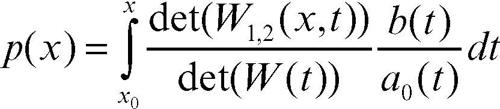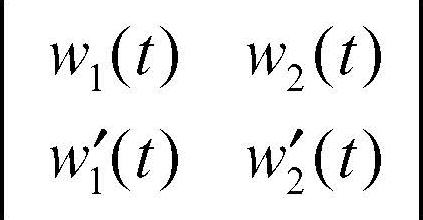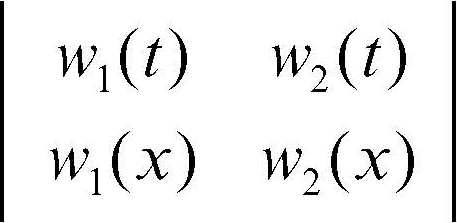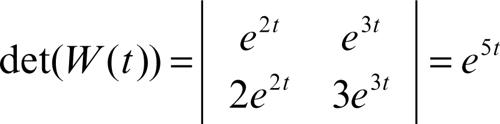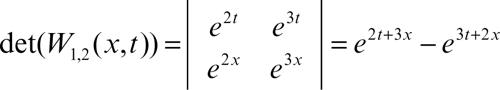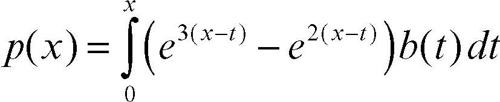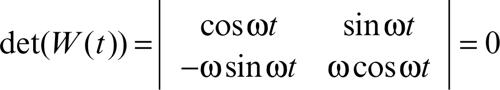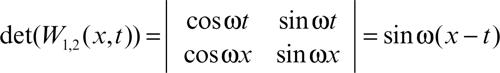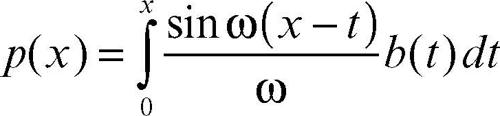equazione differenziale lineare, integrale di una
equazione differenziale lineare, integrale di una
equazione differenziale lineare, integrale di una espressione che, senza ulteriori specificazioni, indica l’integrale generale di un’→ equazione differenziale, che, nel caso qui considerato è lineare. Per individuare l’integrale generale di una equazione differenziale lineare si consideri innanzitutto il caso di una equazione differenziale lineare a coefficienti costanti omogenea. Essa ha la forma:
Le soluzioni di tale equazione sono del tipo y = eλx, con λ radice della cosiddetta equazione caratteristica:
La soluzione dell’equazione differenziale è così ridotta a quella di un’equazione algebrica. Se questa ha radici semplici, si ottiene l’integrale generale prendendo una combinazione lineare a coefficienti arbitrari delle corrispondenti funzioni esponenziali (nel caso di soluzioni complesse non reali si utilizza opportunamente, per maggiore semplicità, la formula di → Eulero). Nel caso di radici multiple, nella determinazione di n soluzioni linearmente indipendenti intervengono anche soluzioni del tipo y = xme λx dove m assume tutti i valori minori della molteplicità della radice, di modo che ogni radice genera un numero di soluzioni linearmente indipendenti uguale al suo ordine di molteplicità. Per esempio (indicando con C1, C2, C3, ... costanti arbitrarie):
• y ″ − 5y ′ + 6y = 0, ha equazione caratteristica λ2 − 5λ + 6 = 0 con radici λ = 2 e λ = 3, e l’integrale generale è y = C1e2x + C2e3x;
• y ″ − 2y ′ + 5y = 0. Dall’equazione λ2 − 2λ + 5 = 0 si ottengono le radici caratteristiche 1 ± 2i, da cui l’integrale generale è y = ex[C1cosx + C2sinx];
• y(3) + y = 0. L’equazione caratteristica λ3 + 1 = 0 ha le radici semplici λ = −1 e λ = (1 ± i√(3))/2, quindi l’ integrale generale è
• y(4) − 2y ″ + y = 0. Le radici di λ4 − 2λ2 + 1 = 0 sono λ = ±1, doppie. L’integrale generale è
• y(4) + 2y ″ + y = 0. Le radici dell’equazione caratteristica λ4 + 2λ2 + 1 = 0 sono λ = ±i, doppie. L’integrale generale è y = cosx[C1 + C2x] + sinx[C3 + C4x];
• y(4) = 0. L’equazione caratteristica è λ4 = 0 che ammette la sola radice λ = 0, con molteplicità 4: di conseguenza l’integrale generale è
• y(4) + y(3) = 0. Le radici dell’equazione caratteristica λ4 + λ3 = 0 sono λ = 0, con molteplicità 3 e λ = −1: di conseguenza l’integrale generale è
• y(4) + y ′ = 0. Le radici dell’equazione caratteristica λ4 + λ = 0 sono λ = 0 e λ = −1, con molteplicità 3: di conseguenza l’integrale generale è
Un caso in cui è possibile determinare esplicitamente l’integrale generale di un’equazione lineare a coefficienti non costanti, è quello dell’equazione di → Eulero
Se si cercano soluzioni della forma y = xλ, da cui y ′ = λxλ−1, y ″ = λ(λ − 1)xλ−2 ecc., e dalle uguaglianze xy ′ = λ, xλ, x 2y ″ = λ(λ − 1)xλ ecc., si evidenzia un fattore comune xλ che si può raccogliere a fattore comune e semplificare, ottenendo un polinomio caratteristico q(λ), la cui espressione analitica è riportata nelle tavole delle equazioni differenziali ordinarie. Se q(λ) = 0 ammette n soluzioni distinte, si ottiene l’integrale generale, altrimenti si debbono aggiungere altri integrali della forma y = xλln|x|, y = xλ(ln|x|)2 ecc., in numero pari alla molteplicità della radice. Per esempio:
• x 2y ″ − 2xy ′ + 2y = 0. Si ha: xλ[λ(λ − 1) − 2λ + 2] = 0. Il polinomio q(λ) = λ2 – 3λ + 2 si annulla per λ = 1 e λ = 2, per cui due soluzioni linearmente indipendenti sono y = x e y = x 2, e l’integrale generale è y = C1x + C2x 2;
• x 2y ″ − 3xy ′ + 4y = 0. Il polinomio caratteristico q(λ) = λ2 − 4λ + 4 ammette la radice λ = 2 doppia. L’integrale generale è y = C1x 2 + C2x 2ln|x|.
Nel caso non omogeneo, tutte e sole le soluzioni si ottengono sommando all’integrale generale dell’equazione omogenea associata un integrale particolare p(x) dell’equazione completa. L’integrale particolare può essere determinato mediante il metodo, cosiddetto di somiglianza o attraverso il metodo di variazione delle costanti arbitrarie. Nel primo caso, per un’equazione a coefficienti costanti, se il termine noto b(x) dell’equazione ha la forma Pk(x)eαx cos(βx), o Pk(x)eαxsin(βx), con Pk(x) polinomio di grado k, si proverà a cercare un integrale particolare della forma xmeαx[Qk(x)cos(βx) + Rk(x)sin(βx)], dove Qk e Rk sono polinomi di grado k a coefficienti indeterminati e m è l’ordine di molteplicità della radice α + i β nell’equazione caratteristica. Se il termine noto è una somma di termini del tipo indicato, per il principio di sovrapposizione (→ equazione differenziale) basterà determinare l’integrale particolare corrispondente a ciascuno degli addendi e quindi prenderne la somma. Riprendendo alcune delle equazioni degli esempi precedenti, si mostra di seguito come si applica il metodo di somiglianza:
• y ″ − 5y ′ + 6y = 6e4x. È k = β = 0, α = 4. Poiché le radici caratteristiche sono λ = 2 e λ = 3, risulta m = 0, si cerca una soluzione del tipo p(x) = Ae4x. Derivando e sostituendo si ha che p(x) è soluzione se vale l’identità A[16 – 20 + 6]e4x ≡ 6e4x, che è soddisfatta per A = 3. L’integrale generale è dunque y = C1e2x + C2e3x + 3e4x;
• y ″ − 5y ′ + 6y = 6x. È k = 1, α = β = 0, m = 0. La forma in cui cercare l’integrale particolare è in questo caso p(x) = Ax + B; si ottiene − 5A + 6Ax + 6B ≡ 6x, da cui A = 1, B = 5/6. Se l’equazione fosse y ″ − 5y ′ + 6y = 6e4x + 6x, si potrebbero sommare questi due risultati, ottenendo l’integrale generale nella forma y = C1e2x + C2e3x + 3e4x + x + 5/6;
• y ″ − 5y ′ + 6y = e2x. È k = β = 0, α = 2, che in questo caso è una radice caratteristica. Pertanto si pone y = Axe2x e, sostituendo, si ottiene A = −1 ;
• y(4) + 2y ″ + y = 27xcos2x. Cercando in questo caso una soluzione della forma
si determinano A = D = 0, B = 3, C = −8: risulta cioè p(x) = 3xcos2x − 8 sin2x;
• y(4) + 2y ″ + y = cosx. È k = α = 0, β = 1, e di nuovo si ha una radice caratteristica, ma doppia. Infatti cosx e xcosx sono integrali particolari dell’omogenea; la candidata soluzione è del tipo x 2[Acosx + Bsinx]. Sostituendo si ottiene A = −1/8, B = 0 (questo secondo valore è dovuto al fatto che l’equazione contiene solo le derivate pari; in generale risulta anche B ≠ 0);
• y(4) = x + 8. Si ha k = 1, α = β = 0, m = 4. Sia y = x 4Q1(x) = Ax 5 + Bx 4. Si trova A = 1/120, B = 1/3, e l’integrale generale è
Noto l’integrale generale dell’equazione omogenea, che dipende da un numero di costanti arbitrarie pari all’ordine dell’equazione, il metodo di variazione delle costanti arbitrarie consiste nei seguenti due passi: a) far variare tali costanti, che pertanto vanno pensate come funzioni della variabile indipendente; b) cercare un integrale particolare di questa forma, in modo da identificare tali coefficienti, imponendo di volta in volta, nei calcoli necessari per sostituire il prototipo di soluzione nell’equazione, condizioni sui coefficienti che permettano di semplificare i conti ma non siano troppo restrittive.
Con coefficienti generici, non è possibile determinare analiticamente l’integrale generale di un’equazione differenziale lineare neppure del secondo ordine e neanche nel caso omogeneo (per quelle del primo ordine si veda → equazione differenziale, integrale di una). Se tuttavia per un’equazione del secondo ordine omogenea, a0(x)y″ + a1(x)y′ + a2(x)y = 0, si conosce un integrale particolare w(x), è possibile trovarne un secondo mediante la formula
e quindi scrivere l’integrale generale nella forma y = C1w(x) + C2v(x). Alcuni casi in cui si può ottenere l’integrale w(x) sono i seguenti:
• se per qualche k risulta a0(x)k 2 + a1(x)k + a2(x) = 0, allora w(x) = ekx è un integrale particolare; per esempio l’equazione differenziale xy ″ − y ′ + (1 − x)y = 0 ammette w(x) = ex come soluzione; quindi una seconda soluzione è
e l’integrale generale è y = C1ex + C2(2x + 1)e–x;
• l’equazione a0(x)y ″ + k(xy ′ − y) = 0 ammette la soluzione w(x) = x.
In genere, se si conosce un integrale particolare w(x) di un’equazione lineare di ordine n, la sostituzione y(x) = w(x)z(x) la riduce a una di ordine n − 1 nell’incognita z ′.
Per la ricerca di un integrale particolare dell’equazione completa, si fornisce di seguito la formula nel caso di ordine 2, a0(x)y ″ + a1(x)y ′ + a2(x)y = b(x), avvertendo che si generalizza a un ordine qualsiasi. Se y = C1w1(x) + C2w2(x) è l’integrale generale dell’equazione omogenea associata, un integrale particolare è dato da:
dove det(W(t)) è il determinante wronskiano (→ matrice wronskiana)
e det(W 1,2(x, t)) è il determinante
Tale integrale soddisfa il problema di Cauchy p(x0) = p′ (x0) = 0. La scelta di x0 è arbitraria, purché in tale punto le funzioni siano continue. Per esempio (si noti la struttura di prodotto di → convoluzione della soluzione ottenuta):
• per l’equazione y» − 5y ′ + 6y = b(x) si ha
quindi la formula fornisce
• per y ″ + ω2y = b(x) si ha:
quindi
