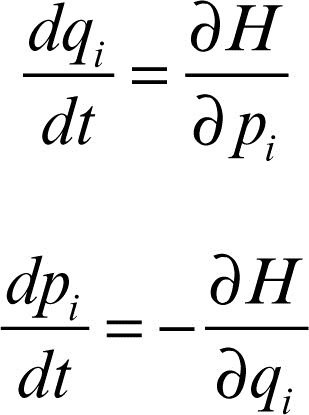Hamilton, equazioni di

Hamilton, equazioni di

Hamilton, equazioni di nelle applicazioni della matematica alla fisica, equazioni del moto di un sistema meccanico, espresse in una particolare forma frequentemente utilizzata in meccanica analitica. Se si individua lo stato di un sistema meccanico con n gradi di libertà mediante n coordinate generalizzate q₁, q₂, …, q_n, dette coordinate di → Lagrange, e n momenti coniugati p₁, p₂, …, p_n, le equazioni di Hamilton hanno la forma (con i = 1, 2, …, n)

dove H = H(q₁, q₂, …, q_n; p₁, p₂, …, p_n; t) è la cosiddetta funzione hamiltoniana del sistema e in alcuni casi rappresenta l’energia totale del sistema. Se H non dipende esplicitamente dal tempo t, l’energia del sistema si conserva durante il moto. Dalle equazioni di Hamilton si deduce che, se H non dipende da una coordinata q_i, il corrispondente momento coniugato p_i è una costante del moto e, viceversa, una coordinata si mantiene costante nel tempo se il suo momento coniugato non compare in H. Se il sistema si trova in un campo di forze indipendente dal tempo, H è semplicemente data dalla somma dell’energia cinetica e dell’energia potenziale del sistema stesso.