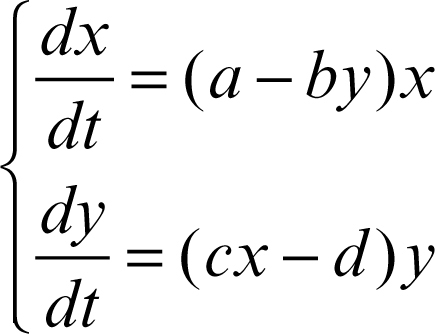Lotka-Volterra, equazioni di

Lotka-Volterra, equazioni di

Lotka-Volterra, equazioni di sistema di equazioni differenziali che costituiscono un modello che descrive l’evoluzione nel tempo di due popolazioni che vivono nello stesso habitat e sono tra loro in una relazione di preda-predatore. Il modello fu elaborato indipendentemente da A.J. Lotka e V. Volterra, e presenta la seguente forma:

in cui x è il numero di individui della popolazione predatore (che si nutre esclusivamente delle prede) al tempo t, y quello degli individui prede al tempo t (che si nutrono di altro, per esempio di vegetali), a, b, c, d parametri reali positivi legati ai tassi di natalità e di mortalità e al fabbisogno di prede da parte dei predatori per unità di tempo. Poiché la sopravvivenza dei predatori dipende dall’esistenza delle prede, il modello mostra che le due popolazioni seguono un andamento oscillante ciclico che non porta all’estinzione di nessuna delle due specie.