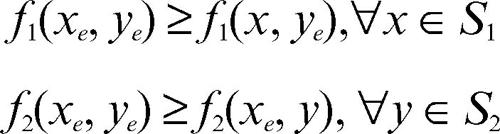Nash, equilibrio di

Nash, equilibrio di

Nash, equilibrio di in teoria dei giochi e nelle applicazioni della matematica all’economia, insieme di strategie, attuate da più giocatori in un gioco non cooperativo, ciascuna delle quali costituisce, per l’individuo che l’ha scelta dal proprio insieme, la strategia ottima, ossia quella che massimizza l’utilità dell’individuo stesso; tutti i soggetti in gioco mirano a un utile individuale e tuttavia possono trovare un punto di equilibrio.

Più formalmente e considerando per semplicità un gioco con due soli giocatori, un gioco è caratterizzato da:

• due giocatori, indicati con 1 e 2;

• due strategie, cioè due insiemi delle scelte possibili in ogni stato del gioco, S₁ per il primo giocatore, S₂ per il secondo;

• due funzioni ƒ₁, ƒ₂: S₁ × S₂ → R che esprimono rispettivamente le vincite dei due giocatori in funzione della combinazione delle due strategie messe in atto dai giocatori (la vincita di un giocatore dipende infatti non solo dalla sua strategia, ma anche dalle strategie scelte dagli avversari).

Si definisce allora equilibrio di Nash ogni coppia di strategie (x_e, y_e) ∈ S₁ × S₂ tali che:

Queste disuguaglianze (che possono essere generalizzate al caso di n giocatori) significano che, se un gioco ammette almeno un equilibrio di Nash, ogni giocatore ha a disposizione almeno una strategia di equilibrio dalla quale non ha alcun interesse ad allontanarsi se tutti gli altri giocatori hanno giocato la propria strategia di equilibrio. Se infatti, per esempio, il giocatore 1 non giocasse la strategia x_e mentre l’altro giocatore giocasse la strategia y_e egli potrebbe soltanto peggiorare la propria vincita o, al più, lasciarla invariata.

Nash ha dimostrato l’esistenza di un tale equilibrio quando gli insiemi delle strategie per gli n individui e le loro funzioni di utilità soddisfano delle condizioni abbastanza blande. Poiché, da un punto di vista formale, n insiemi di strategie e n corrispondenti funzioni di utilità costituiscono un gioco con n individui, si può dire che la nozione di equilibrio di Nash generalizza al caso di n giocatori la nozione di equilibrio per un gioco tra due individui e a somma zero, introdotta da J. von Neumann e O. Morgenstern (→ giochi, teoria dei), e che la dimostrazione di esistenza di Nash generalizza similmente il celebre teorema di questi autori sull’esistenza di un equilibrio, con strategie miste, per qualsiasi gioco tra due individui a somma zero. Nash ha infatti dimostrato che ogni gioco non cooperativo finito (cioè con un numero finito di giocatori e insiemi di strategie finite) a strategie miste ammette almeno un equilibrio di Nash. Un gioco a strategie miste è un gioco in cui di fronte a diverse scelte si opera in base a valutazioni di probabilità.

La nozione di equilibrio di Nash si è rivelata molto importante anche nell’analisi, positiva piuttosto che normativa, di situazioni in cui gli individui prendono le loro scelte tenendo conto delle scelte prese dagli altri (a differenza di quanto avviene, per esempio, nei mercati di concorrenza perfetta), ma senza pensare di influire gli uni sulle scelte degli altri o di mettersi d’accordo (cooperare), formando delle coalizioni. E ciò sia per difficoltà d’informazione sia per mancanza di fiducia reciproca. Un equilibrio di Nash può essere visto semplicemente anche come un insieme di n azioni che nessuno degli n individui ha interesse a modificare; da questo punto di vista, può essere utilmente confrontato con una situazione formata da n azioni che la coalizione di tutti gli individui non abbia interesse a modificare.

Nash ha proposto due interpretazioni del concetto di equilibrio: una basata sulla razionalità e l’altra sulle popolazioni statistiche. Nella prima i giocatori sono considerati razionali; possiedono una completa informazione sulla struttura del gioco, comprese le alternative strategiche e le preferenze degli altri giocatori, e possono calcolare la scelta strategica ottima di ciascuno. Se tutti i giocatori si aspettano lo stesso equilibrio, nessuno è incentivato a modificare la propria strategia. La seconda interpretazione ha trovato sviluppi in biologia allo scopo di comprendere come operano i principi della selezione naturale nella interazione strategica all’interno di una specie e tra specie e specie. L’equilibrio di Nash è diventato uno strumento normalmente usato in tutte le aree della teoria economica.