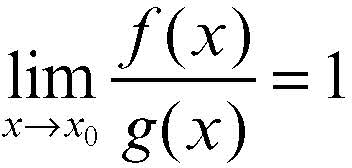equivalenza asintotica

equivalenza asintotica

equivalenza asintotica proprietà di due funzioni ƒ(x) e g(x), definite e non nulle in un intorno di un punto x₀, escluso x₀ dove le funzioni possono annullarsi o non essere definite. Esse, in tali condizioni, si dicono asintoticamente equivalenti se

Si scrive in tal caso ƒ(x) ∼ g(x), per x → x₀. Per esempio, per x → 0 risulta sinx ∼ (e^x − 1) ∼ ln(1 + x) ∼ x, mentre (1 − cosx) ∼ x ²/2. La relazione di equivalenza asintotica è una particolare relazione di equivalenza. Tale relazione si mantiene per cambiamenti di variabile: se h(t) → x₀ per t → t₀, con h(t) ≠ x₀, allora ƒ(h(t)) ∼ g(h(t)) per t → t₀. Per esempio, sostituendo x = 1/t nelle equivalenze precedenti, si ha che per t → ∞ risulta sin(1/t) ∼ ln(1 + 1/t) ∼ 1/t; ponendovi x = 2t ³ si ha sin(2t ³) ∼ 2t ³, per t → 0 ecc. Se

esiste, finito o infinito, lo stesso avviene per g(x); tuttavia l’equivalenza asintotica specifica molto di più nei casi in cui tale limite valga 0 o ∞, in quanto precisa che le due funzioni sono infinitesime (o infinite) dello stesso ordine, e anzi, con costante 1. Specialmente è utile il caso in cui g sia la parte principale di tale infinitesimo (infinito). Se ƒ(x) ∼ g(x), è lecito sostituire g a ƒ in ogni limite in cui compaia un prodotto o un quoziente di funzioni, valgono cioè anche le equivalenze asintotiche ƒ(x)h(x) ~ g(x)h(x) e ƒ(x)/h(x) ~ g(x)/h(x), mentre nel caso di una somma algebrica la relazione ƒ(x) + h(x) ~ g(x) + h(x) vale solo se non si ha semplificazione delle parti principali. Per esempio, dagli esempi sopra riportati si deduce che

ma non si può dedurre il valore del

perché a numeratore le parti principali, diminuendo e sottraendo, sono uguali. In un caso del genere è indispensabile un’approssimazione migliore delle funzioni coinvolte ed è necessario utilizzare la nozione di → o piccolo, oppure ricorrere alla regola o teorema di de → l’Hôpital.