equivalenza logica

equivalenza logica

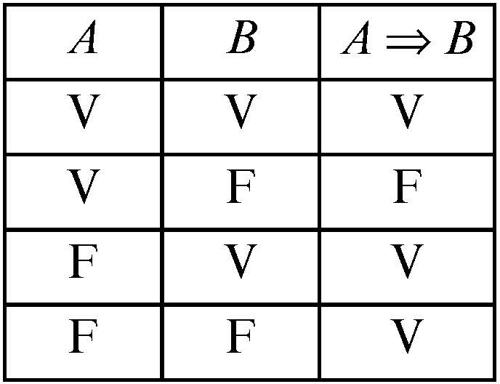
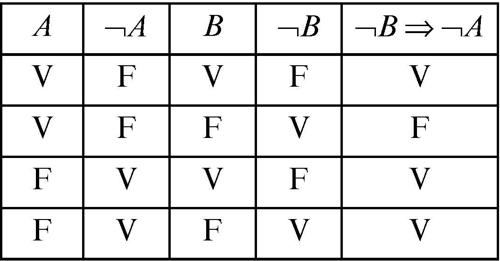
equivalenza logica relazione che lega due enunciati (o, formalmente, due forme enunciative) se questi sono veri o falsi in corrispondenza degli stessi valori di verità delle lettere enunciative che vi compaiono. Si dicono, per esempio, logicamente equivalenti i due enunciati A ⇒ B e ¬B ⇒ ¬A poiché il primo è vero solo nel caso in cui sia vero anche il secondo e viceversa, come è evidente dalla loro rispettive tavole di verità:

Le rispettive ultime colonne delle due tabelle hanno gli stessi valori: i due enunciati composti sono veri o falsi in corrispondenza degli stessi valori di verità degli enunciati che li compongono. In generale si può dedurre l’equivalenza logica di due enunciati esaminando le rispettive tavole di verità: essi sono logicamente equivalenti quando definiscono la stessa funzione di verità.

Si può anche dire che due enunciati A e B sono logicamente equivalenti se l’enunciato A ⇔ B è una tautologia. Più in generale, in un sistema formale S, due formule ben formate α e β si dicono logicamente equivalenti se in S è possibile dimostrare la formula ben formata α ⇔ β. Se in una formula ben formata A si sostituisce una parte con un’altra a essa logicamente equivalente, si ottiene una formula ben formata A′ logicamente equivalente ad A: l’equivalenza logica permette così di sostituire parte di una formula con un’altra a essa logicamente equivalente.