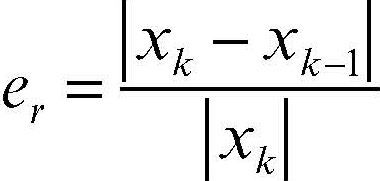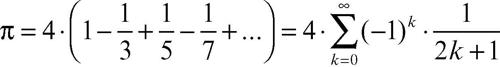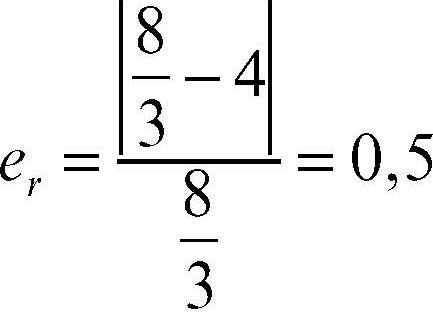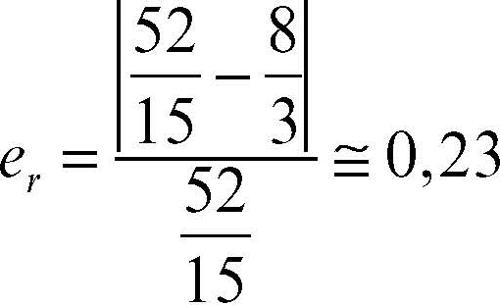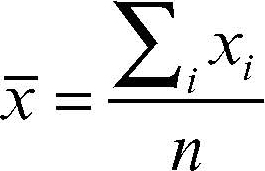errore

errore

errore termine che assume significati diversi nel calcolo numerico, nelle applicazioni della matematica alle scienze sperimentali e in statistica inferenziale.

☐ Nel calcolo numerico è la differenza in valore assoluto tra il valore vero di un numero e una sua rappresentazione approssimata. L’errore può riferirsi a diverse cause:

• ai processi infiniti nell’analisi matematica (per esempio, il calcolo del limite di una successione, il calcolo di una somma infinita ecc.). In tali casi, il processo è infinito ed è quindi inevitabile che, in un calcolo numerico, esso venga interrotto a un certo punto: si parla allora di errore analitico;

• alla rappresentazione dei numeri irrazionali o periodici, che non possono essere mai scritti in modo esatto nel sistema posizionale decimale (errore di rappresentazione). Negli strumenti di calcolo e in qualunque scrittura, non sempre un numero n è rappresentabile in modo esatto perché lo spazio a disposizione è finito e il numero può avere un numero di cifre decimali più elevato di quelle che è possibile scrivere o addirittura infinito, come nel caso dei numeri periodici o irrazionali. Se è dunque possibile scrivere al più t cifre, occorre ridurre a t il numero di cifre, eventualmente infinito, che in teoria rappresentano il numero stesso. Ciò si ottiene essenzialmente con il troncamento (si mantengono le prime t cifre e si cancellano tutte le altre) o con l’arrotondamento (si mantengono le prime t −1 cifre e l’ultima, cioè la t-esima, si lascia invariata oppure si aumenta di un’unità nel caso in cui la prima cifra eliminata è uguale o maggiore di 5). Per esempio, il numero n = 0,1923754…, espresso con quattro cifre significative, risulta pari a n’ = 0,1923 per troncamento e a n″ = 0,1924 per arrotondamento. In ognuno dei due casi si commette un errore, nel primo caso di troncamento, nel secondo di arrotondamento. Se poi nell’elaborazione dei dati, nel calcolare il valore di una formula o nel determinare le soluzioni di un’equazione, occorre eseguire molti calcoli successivi tali errori di approssimazione si amplificano fino, talvolta, a far diventare del tutto privi di senso i risultati ottenuti (→ errore, propagazione di un; → operazione, errore in una).

• all’algoritmo usato dal metodo numerico necessario per risolvere un determinato problema. Questi errori, detti errori algoritmici, dipendono dal tipo e dal numero di operazioni eseguite e talvolta possono essere ridotti scegliendo l’algoritmo più idoneo fra diversi possibili. Per esempio, volendo implementare un algoritmo di soluzione dell’equazione di secondo grado ax 2 + bx + c = 0, le cui soluzioni analitiche sono

con Δ = b2 − 4ac, si potrebbe incontrare il caso in cui

e allora la loro differenza potrebbe essere minore della precisione con cui la macchina può apprezzare la minima variazione dei numeri rappresentati. In tali casi è necessario calcolare una soluzione con la formula standard

mentre l’altra si ottiene a partire dalla relazione

Nel caso in cui il numero sia il risultato di una misurazione, la definizione teorica di errore come differenza in valore assoluto tra la misura ottenuta e il valore vero della grandezza misurata non è operativamente applicabile perché il valore vero non è determinabile. A volte, allora, al posto dell’errore assoluto teorico si considera una sua stima superiore, detta errore assoluto limite, che è definito come quel numero ε per cui il valore vero della grandezza x è compreso tra i due estremi: a – ε ≤ x ≤ a + ε, da cui |x – a| ≤ ε. Il numero a – ε è un’approssimazione per difetto di x, mentre a + ε lo è per eccesso. Per esempio, l’errore assoluto limite del numero 3,14, usato in sostituzione di π, può essere determinato considerando che 3,14 < π < 3,15 e quindi |π – 3,14| < 0,01.

Il numero 0,01 è una stima superiore dell’errore assoluto e può essere considerato quindi come errore assoluto limite per π. Se si vuole tenere conto dell’ordine di grandezza, si considera anche l’errore relativo limite, come rapporto tra l’errore assoluto limite e il numero approssimato:

Quando si applicano metodi numerici iterativi, in cui a ogni passo k del calcolo si ottiene un’approssimazione del valore vero x_k sempre migliore, si può considerare, seppure con molta cautela, come stima dell’errore del metodo iterativo la differenza in valore assoluto tra il valore dell’ultima approssimazione ottenuta e l’approssimazione del passo precedente: e = |x_k − x_k–1|.

L’errore relativo del metodo iterativo è allora:

Per esempio, se si utilizza il metodo di Leibniz per il calcolo di π, per cui

si può realizzare un algoritmo iterativo che approssimi il risultato calcolando la (k − 1)-esima somma parziale ottenuta e aggiungendo di volta in volta il termine k-esimo; in tal modo si ottiene una successione di numeri razionali convergenti a π:

L’errore relativo al primo passo del calcolo risulta

mentre al secondo passo è uguale a

ed esso diminuisce uniformemente all’aumentare del numero delle iterazioni.

☐ Nelle applicazioni della matematica alle scienze sperimentali, l’errore indica la differenza tra il valore misurato di una determinata grandezza e il valore vero, dove per «valore vero» si intende un valore teorico, supposto esistente anche se non calcolabile, oppure un valore reale direttamente calcolabile che tuttavia motivi di costo o di opportunità inducono a stimare.

Vi sono due tipi di errori, quelli sistematici e quelli accidentali (o casuali). Gli errori sistematici sono dovuti a una caratteristica intrinseca dello strumento, per esempio la cattiva qualità, la errata taratura o l’inadeguatezza alla misura in questione, oppure all’eventuale imperizia dello sperimentatore. Caratteristica degli errori sistematici è di influire in genere sempre nello stesso senso e nella stessa maniera in successive ripetizioni dell’osservazione; tali errori si possono ridurre o eliminare dedicando la massima cura all’esperimento che si intende eseguire. Spesso tali errori si scoprono e si correggono utilizzando due metodi diversi per misurare la stessa grandezza; altre volte, e quando se ne conosce l’origine, si correggono anche attraverso il calcolo. Per questo tipo di errori non vi è però una teoria generale e in una misura corretta essi si intendono generalmente eliminati. Gli errori accidentali o casuali sono invece dovuti al fatto che gli strumenti di misura rilevano gli effetti sulla grandezza da misurare di molteplici fattori esterni, per cui misurazioni successive della stessa grandezza effettuate con strumenti di sufficiente sensibilità danno risultati di misura generalmente diversi. Gli errori casuali di una misurazione possono influire sulla misura ora in un senso ora in un altro e con entità variabile da una misura all’altra. Dal momento che tali errori influenzano il risultato della misura ora in un senso ora nell’altro, le loro frequenze generalmente si distribuiscono con un andamento che approssima la → curva normale e ci si deve ragionevolmente aspettare che il valore medio calcolato sui risultati di un gran numero di ripetizioni della misura risenta poco delle cause di variabilità e si avvicini di più al valore vero, cioè sia affetto da un minore errore casuale. E infatti, se si indica con x̄ il valore medio dei risultati di n misure x_i della stessa grandezza X, cioè se si ha

dove x_i è il risultato della i-esima misura di X, al crescere del numero delle misure il valore x̄ tende a stabilizzarsi sempre più intorno al valore vero x0; quindi, quando il numero n delle misure è sufficientemente grande, si considera x̄ come una buona approssimazione di x0 e x̄ è detto misura attendibile. Se si indicano rispettivamente con xmax e xmin le misurazioni massime e minime ottenute per la stessa grandezza X, una prima valutazione dell’errore commesso è data da

che è detto errore assoluto. Il risultato della misura sarà allora così espresso:

Poiché l’influenza dell’errore dipende dall’ordine di grandezza della grandezza misurata, accanto all’errore assoluto si considera anche l’errore relativo e_r così definito:

Analogo è il significato di errore in una indagine statistica condotta su un campione: è la differenza tra il valore del parametro di una popolazione (per esempio, l’età media se si tratta di una popolazione di viventi) e una sua stima costruita a partire dai dati campionari. In tale caso esso può essere di campionamento oppure di stima. L’errore di campionamento, essendo connesso al processo stesso di estrazione del campione, è impossibile da eliminare e varia al variare delle unità che entrano a far parte del campione, mentre l’errore di stima è valutabile se si possono fare ragionevoli ipotesi sulla distribuzione della popolazione (per esempio → distribuzione normale) e se ne conosce lo scarto quadratico medio (→ errore standard; → scarto).

☐ In statistica inferenziale, nella → verifica delle ipotesi, si commette un errore quando un test statistico campionario induce a valutare una ipotesi relativa a un determinato fenomeno in modo non corrispondente alla realtà dei fatti. In linea generale, quando ci si pone una domanda relativa a un determinato fenomeno (per esempio: l’automobile A consuma di più dell’automobile B? L’uso del dentifricio X riduce l’insorgere di carie? La durata media di uno pneumatico per automobili è 40.000 km?) essa può essere tramutata in un’ipotesi di base, detta ipotesi nulla e indicata con H0, formulata in base a principi di indifferenza, cui si contrappone una ipotesi alternativa, indicata con H1. Nei casi precedenti, le ipotesi nulle potrebbero essere: «l’automobile A consuma tanto quanto l’automobile B»; «l’uso del dentifricio X riduce l’insorgere di carie»; «la durata media di uno pneumatico per automobili è di 40.000 km». Sottoponendo tale ipotesi nulla a una verifica (una prova su strada, un test clinico, un’indagine campionaria), è possibile sia che occorra accettare tale ipotesi iniziale sia che essa vada rifiutata. Qualunque siano le modalità con cui sono realizzate, tali verifiche, spesso effettuate su un campione limitato, sono però soggette a errore. In linea di principio, sono quindi possibili quattro situazioni diverse:

• l’ipotesi nulla è vera, ma la verifica effettuata indica che essa va rifiutata (in tale caso si commette un errore, detto errore di prima specie);

• l’ipotesi iniziale è falsa, ma la verifica effettuata indica che essa va accettata (in tale caso si commette un errore, detto errore di seconda specie);

• l’ipotesi iniziale è vera e la verifica indica che essa va accettata (nessun errore);

• l’ipotesi iniziale è falsa e la verifica indica che essa va rifiutata (nessun errore).

Le quattro situazioni sono sintetizzate nella tabella. La verifica delle ipotesi nell’inferenza statistica si occupa di analizzare tale casistica. Si fa riferimento a un campione (che assume il ruolo di esperimento) in base al quale è possibile fare delle considerazioni e verificare le ipotesi formulate sulla popolazione di partenza. La regola di decisione quantitativa che porta all’accettazione o al rifiuto dell’ipotesi nulla è legata a un determinato livello di → significatività, solitamente indicato con α. Tale valore, generalmente fissato a priori, corrisponde alla probabilità di commettere un errore di prima specie. Se per esempio è stato scelto un livello di significatività α = 5%, ciò vuol dire che si ha il 5% di probabilità di rifiutare un’ipotesi che in realtà è vera. Il numero1 – α rappresenta invece il livello di → confidenza, cioè la fiducia che si ha nel non commettere alcun errore nell’accettare l’ipotesi nulla se i dati campionari avvalorano tale ipotesi. La probabilità di commettere un errore di seconda specie è invece generalmente indicata con β; il complemento a uno di β, cioè γ = 1 – β è detto potenza del test e indica la probabilità di rifiutare l’ipotesi nulla quando essa è falsa.